Dagger category
In mathematics, a dagger category (also called involutive category or category with involution ) is a category equipped with a certain structure called dagger or involution. The name dagger category was coined by Selinger.
Formal definition
A dagger category is a category  equipped with an involutive functor
equipped with an involutive functor  that is the identity on objects, where
that is the identity on objects, where  is the opposite category.
is the opposite category.
In detail, this means that it associates to every morphism  in
in  its adjoint
its adjoint  such that for all
such that for all  and
and  ,
,



Note that in the previous definition, the term "adjoint" is used in a way analogous to (and inspired by) the linear-algebraic sense, not in the category-theoretic sense.
Some sources define a category with involution to be a dagger category with the additional property that its set of morphisms is partially ordered and that the order of morphisms is compatible with the composition of morphisms, that is a<b implies  for morphisms a, b, c whenever their sources and targets are compatible.
for morphisms a, b, c whenever their sources and targets are compatible.
Examples
 in Rel, the relation
in Rel, the relation  is the relational converse of
is the relational converse of 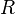 . In this example, a self-adjoint morphism is a symmetric relation.
. In this example, a self-adjoint morphism is a symmetric relation.Podcasts:

