Latest News for: covering relation
Edit
Momentum now offers insurance for GNU meeting cancellations
Business Day 01 Apr 2025
GeNiUs is an exciting new type of insurance that will cover clients for losses pertaining to planned events related to, and as a result of, cancelled government meetings and postponed announcements.
Edit
 Beaumont Enterprise
01 Apr 2025
Beaumont Enterprise
01 Apr 2025
Cyprus Israelis Rape Case
 Beaumont Enterprise
01 Apr 2025
Beaumont Enterprise
01 Apr 2025
FILE - A relative of one from five Israelis who are accused of raping a British woman, cover her face with a bag as leaves the building of the Famagusta District Courthouse in Paralimni, Cyprus, Tuesday, Sept. 12, 2023 ....
Edit
Parents caring for children with severe disabilities to be covered by social security contributions
The Malta Independent 01 Apr 2025
Prime Minister Robert Abela said that parents of children with severe disabilities who receive the Carer's grant which supports such families will now also be covered by accredited social security contributions.
Edit
This bill aims to help firefighters with cancer. Getting it passed is just the beginning
The Los Angeles Times 01 Apr 2025
... Public Safety Officers’ Benefits Program if it adds to the conditions currently covered, noting that the 9/11 programs have swelled as more first responders have presented service-related conditions.
Edit
Children over the moon after receiving Eidi gifts
Urdu Point 01 Apr 2025
... to see wildlife.</p><p>Anaya Bibi (10), a resident of Wapda Town Peshawar remarked, “Eidi from my relatives helped cover the costs of tickets for the swings, food, and transport.
Edit
Bright Regency mews off Leeson Street in Dublin city centre for €860,000
The Irish Times 01 Apr 2025
Edit
298 persons killed in Wayanad landslides: Govt informs Parliament
Madhyamam 01 Apr 2025
This amount covers expenses for using Indian Air Force (IAF) helicopters in rescue and relief efforts, as well as for debris clearance, as per actual costs incurred.
Edit
Mattoon council may implement city manager government, appoint Gill as interim manager
Journal Gazette 01 Apr 2025
Edit
Azincourt Energy to conduct geophysics at East Preston Uranium Project, Saskatchewan
Resource World 01 Apr 2025
East Preston is near the southern edge of the western Athabasca Basin, where targets are in a near surface environment without Athabasca sandstone cover – therefore they are relatively shallow targets but can have great depth extent when discovered.
Edit
SLB contracted to drill ultra-deep-water wells for Trion project offshore Mexico
Offshore Technology 01 Apr 2025- 1
- 2
- Next page »


 be a set with a partial order
be a set with a partial order  .
As usual, let
.
As usual, let  be the relation on
be the relation on  if and only if
if and only if  and
and  .
.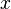 and
and  be elements of
be elements of  ,
if
,
if  such that
such that  . Equivalently,
. Equivalently, ![[x,y]](http://assets.wn.com/wiki/en/1/46/8ca042e8ff30aba99a78e-fd2fef.png) is the two-element set
is the two-element set  .
.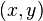 in the covering relation.
in the covering relation.