Susana
Susana may refer to:
See also

Susana (film)
Susana (Susana, demonio y carne or The Devil and the Flesh) is a 1951 film directed by Luis Buñuel. It is the story of a girl of questionable mental stability who escapes from incarceration and ends up at a plantation where she disrupts a working family's daily routines and chemistry.
Plot
Susana is full of the unique touches of Buñuel's surrealism. The heroine, Susana (Rosita Quintana), is a beautiful inmate at a women's reformatory who escapes in the middle of a rainy night. When first seen, Susana's being thrown into a solitary cell for misbehaving and the correction officer says Imagine, she's been here two years and is worse than ever!.
In her cell she asks God's help, facing a shadow of the cross formed by the window bars from where a spider crawls away. The window breaks open and she escapes. She ends up at a ranch. Soon the whole household is involved in possessing her and fighting over her. Jesus, the young ranch helper; Alberto, the family's son and heir; and Guadalupe, Alberto's father, 'a God-fearing man and the faithful husband of the beautiful, patient Dona Carmen'.
Susana (given name)
Susana is a feminine given name. Like its variants, which include the names Susanna and Susan, it is derived from Σουσάννα, Sousanna, the Greek form of the Hebrew שושנה, Shoshannah, which could have been derived from the Aramaic language. ܫܘܫܢ, Shoshan means lily in Syriac. سوسن, Susan, is the Persian spelling of this name. The spelling Susanna is used in Sweden, Italy, the Netherlands and Finland, as well as much of the English-speaking world. Zuzana is used in Czech Republic and Slovakia, and the spelling is Zsuzsanna in Hungary. In Polish it is Zuzanna. In addition to its use in English, the spelling Susana is also common in countries such as Spain and Portugal.
Authors, poets and writers
Connection
Connection may refer to:
Technology
Mathematics
Connection (principal bundle)
In mathematics, a connection is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. A principal G-connection on a principal G-bundle P over a smooth manifold M is a particular type of connection which is compatible with the action of the group G.
A principal connection can be viewed as a special case of the notion of an Ehresmann connection, and is sometimes called a principal Ehresmann connection. It gives rise to (Ehresmann) connections on any fiber bundle associated to P via the associated bundle construction. In particular, on any associated vector bundle the principal connection induces a covariant derivative, an operator that can differentiate sections of that bundle along tangent directions in the base manifold. Principal connections generalize to arbitrary principal bundles the concept of a linear connection on the frame bundle of a smooth manifold.
Formal definition
Let π:P→M be a smooth principal G-bundle over a smooth manifold M. Then a principal G-connection on P is a differential 1-form on P with values in the Lie algebra  of G which is G-equivariant and reproduces the Lie algebra generators of the fundamental vector fields on P.
of G which is G-equivariant and reproduces the Lie algebra generators of the fundamental vector fields on P.
Connection (affine bundle)
Let  be an affine bundle modelled over a vector bundle
be an affine bundle modelled over a vector bundle
 . A connection
. A connection 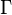 on
on  is called the affine connection if it as a section
is called the affine connection if it as a section  of the jet bundle
of the jet bundle  of
of  is an affine bundle morphism over
is an affine bundle morphism over  . In particular, this is the case of an affine connection on the tangent bundle
. In particular, this is the case of an affine connection on the tangent bundle  of a smooth manifold
of a smooth manifold  .
.
With respect to affine bundle coordinates  on
on  , an affine connection
, an affine connection 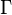 on
on  is given by the tangent-valued connection form
is given by the tangent-valued connection form
An affine bundle is a fiber bundle with a general affine structure group  of affine transformations of its typical fiber
of affine transformations of its typical fiber  of dimension
of dimension  . Therefore, an affine connection is associated to a principal connection. It always exists.
. Therefore, an affine connection is associated to a principal connection. It always exists.
For any affine connection  , the corresponding linear derivative
, the corresponding linear derivative  of an affine morphism
of an affine morphism 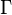 defines a
unique linear connection on a vector bundle
defines a
unique linear connection on a vector bundle  . With respect to linear bundle
coordinates
. With respect to linear bundle
coordinates  on
on  , this connection reads
, this connection reads
Since every vector bundle is an affine bundle, any linear connection on a vector bundle also is an affine connection.
If  is a vector bundle, both an affine connection
is a vector bundle, both an affine connection 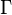 and an associated linear connection
and an associated linear connection  are
connections on the same vector bundle
are
connections on the same vector bundle  , and their
difference is a basic soldering form on
, and their
difference is a basic soldering form on  . Thus, every affine
connection on a vector bundle
. Thus, every affine
connection on a vector bundle  is a sum of a linear
connection and a basic soldering form on
is a sum of a linear
connection and a basic soldering form on  .
.
Podcasts:

Latest News for: connection susana
- 1
