Tweet this page share on Facebook

Thursday, 27 March 2025

Wiki

Superfly
Superfly (band)
Curtis Mayfield
Connection
Connection (principal bundle)
Connection (affine bundle)

Bing

Superfly

Superfly or Super fly may refer to:

Film and music

Super Fly (film), a 1972 blaxploitation film

Super Fly (soundtrack), a 1972 Curtis Mayfield soundtrack to the film
"Superfly" (song), the album's title track

Super Fly (soundtrack), a 1972 Curtis Mayfield soundtrack to the film

"Superfly" (song), the album's title track

"Super Fly" (Giant Panda song), a 2005 single by Giant Panda

"Superfly", a song by 4 Non Blondes on their only album Bigger, Better, Faster, More!

"Superfly", a song on The O.C. Supertones' sixth album Hi-Fi Revival

Superfly (band) (born 1984), Japanese rock unit, formerly a duo

Superfly (Superfly album), the rock unit's debut self-titled album

Superfly (Superfly album), the rock unit's debut self-titled album

People

Frank "Superfly" Lucas (born 1930), Harlem crime figure and inspiration for the film American Gangster

"Superfly" Jimmy Snuka (born 1943), retired professional wrestler noted for his risk-taking performances

Super Fly (wrestler) (born 1987), Mexican professional wrestler

This page contains text from Wikipedia, the Free Encyclopedia - https://wn.com/Superfly

Superfly (band)

Superfly is a Japanese rock act that debuted on April 4, 2007. Formerly a duo, the act now consists solely of lyricist and vocalist Shiho Ochi with former guitarist Kōichi Tabo still credited as the group's composer and part-time lyricist. Superfly's first two studio albums have been certified double platinum by the Recording Industry Association of Japan, and their four albums (the third being classified as a "single" by the group) all debuted at the top of the Oricon's Weekly Album Charts, a first for a female recording artist in Japan in over seven years.

History

2003–2006: Formation

Shiho Ochi (越智志帆, Ochi Shiho) met Kōichi Tabo (多保孝一, Tabo Kōichi) in 2003 while they were students at Matsuyama University. They were both members of a music circle that covered songs by Finger 5 and the Rolling Stones. In 2004, the group formed the blues band "Superfly", naming themselves after Curtis Mayfield's song "Superfly". The group disbanded in 2005, with only Ochi and Tabo remaining when they went to Tokyo to seek out a label.

This page contains text from Wikipedia, the Free Encyclopedia - https://wn.com/Superfly_(band)

Curtis Mayfield

Curtis Lee Mayfield (June 3, 1942 – December 26, 1999) was an American soul, R&B, and funk singer-songwriter, guitarist, and record producer, who was one of the most influential musicians behind soul and politically conscious African-American music. He first achieved success and recognition with The Impressions during the Civil Rights Movement of the late 1950s and 1960s, and later worked as a solo artist.

Born in Chicago, Illinois, Mayfield started his musical career in a gospel choir. Moving to Chicago's North Side he met Jerry Butler in 1956 at the age of 14, and joined vocal group The Impressions. As a songwriter, Mayfield became noted as one of the first musicians to bring more prevalent themes of social awareness into soul music. In 1965, he wrote "People Get Ready" for The Impressions, which displayed his more politically charged songwriting. Ranked at no. 24 on Rolling Stone's list of the 500 Greatest Songs of All Time, the song received numerous other awards, and was included in the Rock and Roll Hall of Fame 500 Songs that Shaped Rock and Roll, as well as being inducted into the Grammy Hall of Fame in 1998.

This page contains text from Wikipedia, the Free Encyclopedia - https://wn.com/Curtis_Mayfield

Connection

Connection may refer to:

Technology

Database connection

Telecommunication circuit, the complete path between two terminals

Virtual connection, also known as a virtual circuit

Mathematics

Connectedness

Connected sum

Connection (algebraic framework)

Connection (mathematics), a way of specifying a derivative of a geometrical object along a vector field on a manifold

Connection (affine bundle)
Connection (composite bundle)
Connection (fibred manifold)

Connection (affine bundle)

Connection (composite bundle)

Connection (fibred manifold)

Connection (principal bundle), gives the derivative of a section of a principal bundle

Connection (vector bundle), differentiates a section of a vector bundle along a vector field

Cartan connection, achieved by identifying tangent spaces with the tangent space of a certain model Klein geometry

Ehresmann connection, gives a manner for differentiating sections of a general fibre bundle

Electrical connection, allows the flow of electrons

Galois connection, a type of correspondence between two partially ordered sets

This page contains text from Wikipedia, the Free Encyclopedia - https://wn.com/Connection

Connection (principal bundle)

In mathematics, a connection is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. A principal G-connection on a principal G-bundle P over a smooth manifold M is a particular type of connection which is compatible with the action of the group G.

A principal connection can be viewed as a special case of the notion of an Ehresmann connection, and is sometimes called a principal Ehresmann connection. It gives rise to (Ehresmann) connections on any fiber bundle associated to P via the associated bundle construction. In particular, on any associated vector bundle the principal connection induces a covariant derivative, an operator that can differentiate sections of that bundle along tangent directions in the base manifold. Principal connections generalize to arbitrary principal bundles the concept of a linear connection on the frame bundle of a smooth manifold.

Formal definition

Let π:P→M be a smooth principal G-bundle over a smooth manifold M. Then a principal G-connection on P is a differential 1-form on P with values in the Lie algebra $\mathfrak g$ of G which is G-equivariant and reproduces the Lie algebra generators of the fundamental vector fields on P.

This page contains text from Wikipedia, the Free Encyclopedia - https://wn.com/Connection_(principal_bundle)

Connection (affine bundle)

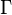Let $Y\to X,$ be an affine bundle modelled over a vector bundle $\overline Y\to X$ . A connection $\Gamma$ on $Y\to X$ is called the affine connection if it as a section $\Gamma:Y\to J^1Y$ of the jet bundle $J^1Y\to Y$ of $Y$ is an affine bundle morphism over $X$ . In particular, this is the case of an affine connection on the tangent bundle $TX$ of a smooth manifold $X$ .

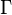With respect to affine bundle coordinates $(x^\lambda,y^i)$ on $Y$ , an affine connection $\Gamma$ on $Y\to X$ is given by the tangent-valued connection form

An affine bundle is a fiber bundle with a general affine structure group $GA(m,\mathbb R)$ of affine transformations of its typical fiber $V$ of dimension $m$ . Therefore, an affine connection is associated to a principal connection. It always exists.

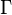For any affine connection $\Gamma:Y\to J^1Y$ , the corresponding linear derivative $\overline\Gamma:\overline Y\to J^1\overline Y$ of an affine morphism $\Gamma$ defines a unique linear connection on a vector bundle $\overline Y\to X$ . With respect to linear bundle coordinates $(x^\lambda,\overline y^i)$ on $\overline Y$ , this connection reads

Since every vector bundle is an affine bundle, any linear connection on a vector bundle also is an affine connection.

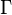If $Y\to X$ is a vector bundle, both an affine connection $\Gamma$ and an associated linear connection $\overline\Gamma$ are connections on the same vector bundle $Y\to X$ , and their difference is a basic soldering form on $\sigma= \sigma_\lambda^i(x^\nu) dx^\lambda\otimes\partial_i$ . Thus, every affine connection on a vector bundle $Y\to X$ is a sum of a linear connection and a basic soldering form on $Y\to X$ .