Latest News for: congruence relation
Edit
Egypt, Djibouti agree to coordinate work at African Union, Arab League
Egypt Today 10 Nov 2024
... levels, building upon on the growth in relations in the past years, which was manifested in the call between the two presidents on October 30 as there was congruence on continuous consultations.
Edit
Congruence Therapeutics Announces Blitz Talk Award And Poster Presentations On MC4R-Deficient Genetic Obesity Program At ...
MENA FN 03 Nov 2024
(MENAFN - PR Newswire). - Congruence has been awarded the Neuroscience Section Blitz Talk Award for transformative research in MC4R-related early-onset genetic obesity - - ... .
Edit
New research reveals an intriguing fact about human visual perception
PsyPost 02 May 2024
A recent study published in the Journal of Vision reveals that humans are better at estimating the motion of objects moving downwards compared to upwards, regardless of the direction relative to gravity.
Edit
Indian realty market expected to touch $1.5 trillion by 2034: Report
Deccan Herald 12 Apr 2024
“We note that a maturing supply side ecosystem that provides regulatory comfort to consumers and congruence among promise and delivery from the developers implying that the upward trend ...
Edit
 The Lawton Constitution
08 Dec 2023
The Lawton Constitution
08 Dec 2023
Cuba leader meets Iran’s supreme leader, opens up the island to Iranian investors
 The Lawton Constitution
08 Dec 2023
The Lawton Constitution
08 Dec 2023
Edit
Durand Line: old contestations and new conflicts
Asiatimes 15 Oct 2023
The steady deterioration in Pakistan-Afghanistan relations over the past year and a half can be traced to the repeated clashes involving the Taliban and the Pakistani military on the Durand Line.
Edit
Aspen-Sopris Ranger District gets contract for station upgrade, but some community members clinging to a ...
Aspen Times 11 Oct 2023
Edit
Aspen-Sopris Ranger District gets contract for station upgrade, but some community members clinging to a different plan
Post Independent 11 Oct 2023
Edit
Egyptian president discusses cooperation with Speaker of the South Korean General Assembly
Egypt Today 09 Oct 2023
Edit
Is Bitcoin’s 4-Year Cycle Pure Coincidence? Analysis
CryptoPotato 05 Sep 2023
But is one phenomenon truly related to the other? Some analysts believe that the asset’s cyclical movements are related to macro conditions. and that the halving schedule’s congruency is pure coincidence.
Edit
Mexico’s old ruling party, PRI, fractures after election loss
The Mercury News 04 Jul 2023
Senators led by former interior secretary Miguel Osorio Chong announced they will form a new group called “Congruence for Mexico.” The new group will not be able to compete in the 2024 presidential elections. Related Articles. World News ..
Edit
RIL could provide 15% return over next few months: Sandip Sabharwal
The Times of India 16 Jun 2023
They were correlated only that rupee depreciation actually helps them because of the export nature of the business, ex of that there is relative congruence in the businesses of IT companies whereas ...
- 1
- 2
- Next page »

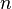
 and
and 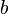 are called congruent modulo
are called congruent modulo  is
is 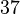 and
and 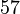 are congruent modulo
are congruent modulo 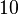 ,
,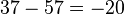 is a multiple of 10, or equivalently since both
is a multiple of 10, or equivalently since both  when divided by
when divided by 