Latest News for: complex algebra
Edit
GROK 3 Agrees That White European Men Are Responsible for Almost All the Greatest Human ...
The Unz Review 12 Mar 2025
... calculations, involving problem-solving by breaking down complex problems into smaller, more manageable parts, and then solving those parts one at a time, using complex algebraic equations.
- 1

 where
where  is a
is a 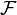 is an algebra over
is an algebra over 