Compact Lie algebra

In the mathematical field of Lie theory, there are two definitions of a compact Lie algebra. Extrinsically and topologically, a compact Lie algebra is the Lie algebra of a compact Lie group; this definition includes tori. Intrinsically and algebraically, a compact Lie algebra is a real Lie algebra whose Killing form is negative definite; this definition is more restrictive and excludes tori, though allowing negative semidefinite includes tori and agrees with the previous definition. A compact Lie algebra can be seen as the smallest real form of a corresponding complex Lie algebra, namely the complexification.

Definition

Formally, one may define a compact Lie algebra either as the Lie algebra of a compact Lie group, or as a real Lie algebra whose Killing form is negative definite. These definitions do not quite agree:

Lie algebra

In mathematics, a Lie algebra (/liː/, not /laɪ/) is a vector space together with a non-associative multiplication called "Lie bracket" . It was introduced to study the concept of infinitesimal transformations. Hermann Weyl introduced the term "Lie algebra" (after Sophus Lie) in the 1930s. In older texts, the name "infinitesimal group" is used.

Lie algebras are closely related to Lie groups which are groups that are also smooth manifolds, with the property that the group operations of multiplication and inversion are smooth maps. Any Lie group gives rise to a Lie algebra. Conversely, to any finite-dimensional Lie algebra over real or complex numbers, there is a corresponding connected Lie group unique up to covering (Lie's third theorem). This correspondence between Lie groups and Lie algebras allows one to study Lie groups in terms of Lie algebras.

Definitions

A Lie algebra is a vector space 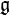over some field F together with a binary operation called the Lie bracket that satisfies the following axioms:

Lie-* algebra

In mathematics, a Lie-* algebra is a D-module with a Lie* bracket. They were introduced by Beilinson & Drinfeld (2004, section 2.5.3), and are similar to the conformal algebras discussed by Kac (1998) and to vertex Lie algebras.

References