Category
Category, plural categories, may refer to:
Philosophy and general uses
Mathematics
- Abelian category
- Category of small categories
- Category of sets
- Category (topology) in the context of Baire spaces
- Lusternik–Schnirelmann category, sometimes called LS-category or simply category
- Monoidal category
- Preadditive category
Linguistics
Lusternik–Schnirelmann category
In mathematics, the Lyusternik–Schnirelmann category (or, Lusternik–Schnirelmann category, LS-category) of a topological space  is the homotopical invariant defined to be the smallest integer number
is the homotopical invariant defined to be the smallest integer number 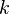 such that there is an open covering
such that there is an open covering  of
of  with the property that each inclusion map
with the property that each inclusion map  is nullhomotopic. For example, if
is nullhomotopic. For example, if  is the circle, this takes the value two.
is the circle, this takes the value two.
Sometimes a different normalization of the invariant is adopted, which is one less than the definition above Such a normalization has been adopted in the definitive monograph by Cornea, Lupton, Oprea, and Tanré (see below).
In general it is not easy to compute this invariant, which was initially introduced by Lazar Lyusternik and Lev Schnirelmann in connection with variational problems. It has a close connection with algebraic topology, in particular cup-length. In the modern normalization, the cup-length is a lower bound for LS category.
It was, as originally defined for the case of X a manifold, the lower bound for the number of critical points that a real-valued function on X could possess (this should be compared with the result in Morse theory that shows that the sum of the Betti numbers is a lower bound for the number of critical points of a Morse function).

Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose objects are sets and whose arrows are functions. On the other hand, any monoid can be understood as a special sort of category, and so can any preorder. In general, the objects and arrows may be abstract entities of any kind, and the notion of category provides a fundamental and abstract way to describe mathematical entities and their relationships. This is the central idea of category theory, a branch of mathematics which seeks to generalize all of mathematics in terms of objects and arrows, independent of what the objects and arrows represent. Virtually every branch of modern mathematics can be described in terms of categories, and doing so often reveals deep insights and similarities between seemingly different areas of mathematics. For more extensive motivational background and historical notes, see category theory and the list of category theory topics.
Podcasts:

-
by Godgory
-
by Godgory
-
by Godgory
-
by Godgory
-
by Godgory
-
by Godgory
-
by Godgory
-
by Godgory
-
by Godgory
-
by Godgory
-
by Godgory
-
by Godgory
-
by Godgory
-
by Godgory
-
by Godgory
-
by Godgory
-
by Godgory
-
by Godgory
-
by Godgory
-
by Godgory
-
by Godgory
-
by Godgory
-
by Godgory
-
by Godgory
-
by Godgory
-
by Godgory
-
by Godgory
-
by Godgory
-
by Godgory
-
by Kettcar
-
by Kettcar
-
by Kettcar
-
by Kettcar
-
by Kettcar
-
by Kettcar
-
by Kettcar
-
by Kettcar
-
by Kettcar
-
by Kettcar
-
by Kettcar
-
by Kettcar
-
by Kettcar
-
by Kettcar
-
by Kettcar
-
by Kettcar
-
by Kettcar
-
by Kettcar
-
by Kettcar
-
by Kettcar
-
by Kettcar
Another Day
by: GodgoryAnother day
When the pains of life won't bar my way
I'll break these chains
That hold me down
I'll tear you down into my private hell
Another day
I will trade my soul for your demise
Trapped in this wheel
I struggle on
Just to make it to another day
No! I won't take no more
no more pain
I'm gonna throw your weight of my back
Put my heart into the attack
I will tear you down
Smash your crown
Have your rule come to an end
And when you finally die by my hand
It's a breath of life to this land
All the wasted years
Come back as tears
In a heavy sigh of relief
Another day
When the dawn breaks over a brand new world
I'll let the sun
Wipe my tears away
Find my peace in the world without end
No! I won't take no more
no more pain
I'm gonna throw your weight of my back
Put my heart into the attack
I will tear you down
Smash your crown
Have your rule come to an end
And when you finally die by my hand
It's a breath of life to this land
All the wasted years
Come back as tears
Latest News for: category 1969
Mets to honor Ed Kranepool with jersey patch this season
- 1
