Boltzmann distribution
In statistical mechanics and mathematics, a Boltzmann distribution (also called Gibbs distribution) is a probability distribution, probability measure, or frequency distribution of particles in a system over various possible states. The distribution is expressed in the form
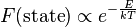
where 
is state energy (which varies from state to state), and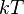 
(a constant of the distribution) is the product of Boltzmann's constant and thermodynamic temperature.
In statistical mechanics, the Boltzmann distribution is a probability distribution that gives the probability that a system will be in a certain state as a function of that state’s energy and the temperature of the system. It is given as
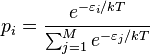
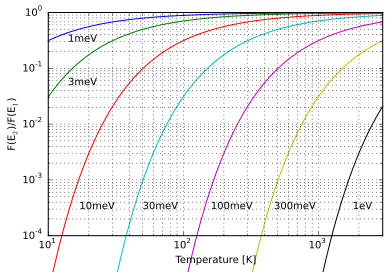
where pi is the probability of state i, εi the energy of state i, k the Boltzmann constant, T the temperature of the system and M is the number of states accessible to the system. The sum is over all states accessible to the system of interest. The term system here has a very wide meaning; it can range from a single atom to a macroscopic system such as a natural gas storage tank. Because of this Boltzmann distribution can be used to solve a very wide variety of problems. The distribution shows that states with lower energy will always have a higher probability of being occupied than the states with higher energy.
Maxwell–Boltzmann distribution
In statistics the Maxwell–Boltzmann distribution is a particular probability distribution named after James Clerk Maxwell and Ludwig Boltzmann. It was first defined and used in physics (in particular in statistical mechanics) for describing particle speeds in idealized gases where the particles move freely inside a stationary container without interacting with one another, except for very brief collisions in which they exchange energy and momentum with each other or with their thermal environment. Particle in this context refers to gaseous particles (atoms or molecules), and the system of particles is assumed to have reached thermodynamic equilibrium. While the distribution was first derived by Maxwell in 1860 on heuristic grounds, Boltzmann later carried out significant investigations into the physical origins of this distribution.
A particle speed probability distribution indicates which speeds are more likely: a particle will have a speed selected randomly from the distribution, and is more likely to be within one range of speeds than another. The distribution depends on the temperature of the system and the mass of the particle. The Maxwell–Boltzmann distribution applies to the classical ideal gas, which is an idealization of real gases. In real gases, there are various effects (e.g., van der Waals interactions, vortical flow, relativistic speed limits, and quantum exchange interactions) that can make their speed distribution different from the Maxwell–Boltzmann form. However, rarefied gases at ordinary temperatures behave very nearly like an ideal gas and the Maxwell speed distribution is an excellent approximation for such gases. Thus, it forms the basis of the Kinetic theory of gases, which provides a simplified explanation of many fundamental gaseous properties, including pressure and diffusion.
Podcasts:
