Biochemical systems theory
Biochemical systems theory is a mathematical modelling framework for biochemical systems, based on ordinary differential equations (ODE), in which biochemical processes are represented using power-law expansions in the variables of the system.
This framework, which became known as Biochemical Systems Theory, has been developed since the 1960s by Michael Savageau and others for the systems analysis of biochemical processes. According to Cornish-Bowden (2007) they "regarded this as a general theory of metabolic control, which includes both metabolic control analysis and flux-oriented theory as special cases".
Representation
The dynamics of a species is represented by a differential equation with the structure:
where Xi represents one of the nd variables of the model (metabolite concentrations, protein concentrations or levels of gene expression). j represents the nf biochemical processes affecting the dynamics of the species. On the other hand, 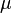 ij (stoichiometric coefficient),
ij (stoichiometric coefficient),  j (rate constants) and fjk (kinetic orders) are two different kinds of parameters defining the dynamics of the system.
j (rate constants) and fjk (kinetic orders) are two different kinds of parameters defining the dynamics of the system.

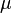 ij (stoichiometric coefficient),
ij (stoichiometric coefficient),  j (rate constants) and fjk (kinetic orders) are two different kinds of parameters defining the dynamics of the system.
j (rate constants) and fjk (kinetic orders) are two different kinds of parameters defining the dynamics of the system.