
Arbelos
In geometry, an arbelos is a plane region bounded by three semicircles connected at the corners, all on the same side of a straight line (the baseline) that contains their diameters.
The earliest known reference to this figure is in the Book of Lemmas by Archimedes, where some of its mathematical properties are stated as Propositions 4 through 8.
Etymology
The name arbelos, used by Archimedes, comes from Greek ἡ ἄρβηλος he árbēlos or ἄρβυλος árbylos, meaning "shoemaker's knife", a knife used by cobblers from antiquity to the current day, whose blade is said to resemble the geometric figure.
Properties
Two of the semicircles are necessarily concave, with arbitrary diameters a and b; the third semicircle is convex, with diameter a+b.
In the following sections, the corners of the arbelos are labeled 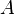 ,
,  , and
, and  , such that the diameter of the outer semicircle is
, such that the diameter of the outer semicircle is  , assumed to have unit length; and the diameters of the inner semicircles are
, assumed to have unit length; and the diameters of the inner semicircles are  and
and  , assumed to have lengths r and 1−r, respectively. The letter
, assumed to have lengths r and 1−r, respectively. The letter  denotes the point where the outer semicircle intercepts the line that is perpendicular to the diameter
denotes the point where the outer semicircle intercepts the line that is perpendicular to the diameter  through the point
through the point 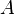 .
.
Podcasts:

-
by Ella Fitzgerald
-
by Peggy Lee
-
by Sarah Vaughan
-
by Madeleine Peyroux
-
by Sebastian Sturm
You're Blase
by: Ella FitzgeraldYou're deep just like a chasm
You've no, enthusiasm
You're tired and uninsipired.
You're blase.
Your day is one of leisure
In which you search for pleasure.
You're bored when you're adored.
You're blase.
While reaching for the moon,
And the stars up in the sky,
The simple things of normal life
Are slowly passing by.
You sleep, the sun is shining;
You wake, its time for dining.
There's nothing new for you to do
You're blase.
instrumental interlude
While reaching for the moon,
And the stars up in the sky,
The simple things of normal life
Are slowly passing by.
You sleep, the sun is shining;
You wake, its time for dining.
There's nothing new for you to do
You're blase.
Blase.
