Latest News for: adapted process
Edit
After What House Of The Dragon Boss Says George R.R. Martin Was ‘Unwilling To Acknowledge,’ I Need To Know How Faithful Season 3 Will Be To Fire And Blood
Cinema Blend 01 Apr 2025
While that doesn't mean a premiere before the end of the 2025 TV schedule, the HBO adaptation of George R.R ... I will simply say, I made every effort to include George in the adaptation process.
Edit
George R.R. Martin didn't see "practical issues" of adapting House Of The Dragon, says Ryan Condal
AV Club 01 Apr 2025
“I will simply say, I made every effort to include George in the adaptation process ... Unfortunately, Condal can’t adapt all 736 pages of the Martin book in their entirety.
Edit
The Abington High softball team needed a catcher this spring. Madison McDonald stepped up
The Patriot Ledger 01 Apr 2025
She adapted quickly to the infield, and now finds herself behind the plate for those same reasons. "She can process the game really quick," Olem said ... they both can adapt super quickly," Howley said.
Edit
Weekly Chinese Horoscope (Mar 31 – Apr 06): Predictions for Monkey Zodiac Sign
The Times of India 01 Apr 2025
The speed of your thought processes, combined with your adaptability skills, will make you stand out when tackling problem-solving tasks ... The process of dividing big assignments into smaller sections will decrease the overwhelming nature of studies ... .
Edit
Stress has a sweet spot. 5 tips to help you find it
CNN 01 Apr 2025
They’re there to help us adapt to our world,” she said, noting that for the entirety of human history that is how humans have survived and thrived ... “It’s a remarkable process called cross-adaptation.
Edit
April Fool! Why are some people more gullible than others?
RTE 01 Apr 2025
This was a useful and adaptive processing strategy in our ancestral environment of small, face-to-face groups, where trust was based on life-long relationships ... Many factors, including mood, influence how we process incoming information.
Edit
House of the Dragon showrunner calls George RR Martin's criticism ‘disappointing’: ‘Made every effort to ...
Hindustan Times 01 Apr 2025
The popular American series House of the Dragon season 2 premiered on HBO in August 2024 ... (Also Read ... House of the Dragon showrunner disappointed with George R.R ... I will simply say I made every effort to include George in the adaptation process ... ....
Edit
Best convertible refrigerators: Top 10 picks for energy-efficient and flexible storage solutions
Hindustan Times 01 Apr 2025
They help save energy, adapt to changing storage needs, and maximise convenience ... Additionally, the Multi Inverter Technology enhances cooling performance and energy efficiency by adapting the defrosting process based on usage patterns.
Edit
USA Compounding Pharmacies Market Set to Reach USD 10,659.3 Million by 2034
Pharmiweb 01 Apr 2025
For patients seeking personalized pharmaceuticals, knowing that their medications are produced in compliance with regulatory guidelines is an essential factor in their decision-making process.
Edit
House of the Dragon Showrunner Responds to George R.R. Martin’s Criticisms of HBO Show
Coming Soon 31 Mar 2025
... relaxed form of adaptation due to the book not being a straightforward novel, but rather various historical texts ... “I will simply say, I made every effort to include George in the adaptation process.
Edit
‘House of the Dragon’ Showrunner Confronts George R.R. Martin Tension, Says He Became ‘Unwilling to ...
The Wrap 31 Mar 2025
“I made every effort to include George in the adaptation process ... “At the end of the day, I just have to keep marching not only the writing process forward, but also the practical parts of ...
Edit
NHU IPDI Pioneers the Future Through End-to-End Innovation and Green Technology
GetNews 31 Mar 2025
Our expert team offers formulation optimization and process adaptation services, effectively overcoming issues like polyurethane yellowing and poor weather resistance—delivering superior performance compared to traditional materials.
Edit
Litmus Announces Strategic Partnership With Microsoft to Deliver Seamless Edge-to-Cloud Industrial AI Solutions
ACCESSWIRE 31 Mar 2025
Edit
The promised land? King Lear and the shape of tragedy
RTE 31 Mar 2025
Yet Shakespeare himself was engaging in the adaptation process ... But the many adaptations of the King Lear story remind us that even a seemingly apocalyptic world is not beyond redemption.
Edit
Tiernan gets 1st career goal in 2-1 Angel City win over the Reign
Newsday 31 Mar 2025
“I think just as a group what we’ve realized is in any capacity that we can help create an environment where it becomes a part of our process to be adaptable to whatever we are presented with, we have ...
- 1
- 2
- Next page »

 be a
be a  be an index set with a total order
be an index set with a total order  (often,
(often, 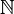 ,
,  ,
, ![[0, T]](http://assets.wn.com/wiki/en/5/17/b74093923941d33ee19be-eb7143.png) or
or  );
); be a
be a 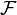 ;
; be a
be a  be a
be a  is said to be adapted to the filtration
is said to be adapted to the filtration  if the
if the  is a
is a  -
- .
.