Abstract
Task-based assessment of image quality in undersampled magnetic resonance imaging (MRI) using constraints is important because of the need to quantify the effect of the artifacts on task performance. Fluid-attenuated inversion recovery (FLAIR) images are used in detection of small metastases in the brain. In this work we carry out two-alternative forced choice (2-AFC) studies with a small signal known exactly (SKE) but with varying background for reconstructed FLAIR images from undersampled multi-coil data. Using a 4x undersampling and a total variation (TV) constraint we found that the human observer detection performance remained fairly constant for a broad range of values in the regularization parameter before decreasing at large values. Using the TV constraint did not improve task performance. The non- prewhitening eye (NPWE) observer and sparse difference-of-Gaussians (S-DOG) observer with internal noise were used to model human observer detection. The parameters for the NPWE and the internal noise for the S-DOG were chosen to match the average percent correct (PC) in 2-AFC studies for three observers using no regularization. The NPWE model observer tracked the performance of the human observers as the regularization was increased but slightly over-estimated the PC for large amounts of regularization. The S-DOG model observer with internal noise tracked human performace for all levels of regularization studied. To our knowledge this is the first time that model observers have been used to track human observer detection for undersampled MRI.
Keywords: Model observers, magnetic resonance imaging, image quality assessment
1. INTRODUCTION
The assessment of image quality in reconstructed MRI images is critical to the development and validation of accelerated reconstruction techniques.1,2 Current methods for assessment of image quality in MRI are largely root mean square error (RMSE) and structural similarity index (SSIM) which are measures of pixel value differences between the original and reconstructed image.3,4 While these measures do give an indication of similarity between images, neither RMSE nor SSIM take into account the specific task for which the image will be used. As a result, images with the same RMSE and SSIM could produce different performance in detection of tumors. Observer models are an alternative way to assess image quality by taking into account human visual principles as well as the task for which the image will be used.
The purpose of this work is to evaluate constrained reconstruction of undersampled MRI data using a TV constraint based on human observer performance in detecting a small signal in a 2-AFC task. Model observers (NPWE and S-DOG) are used to model human observer performance in this detection task. Ultimately, the goal of this work is to reduce the number of future human observer studies needed in this area of research.
2. METHODS
2.1. Undersampled acquisition in MRI
For this study we consider 1-D undersampling of FLAIR images (Figure 1) with a sampling pattern that samples every fourth phase encoding line plus fully sampling the middle 16 kspace lines resulting in an effective acceleration factor of 3.48. Data used in the preparation of this article were obtained from the NYU fastMRI Initiative database5). As such, NYU fastMRI investigators provided data but did not participate in analysis or writing of this report. The reconstruction of the images was done using the Berkeley Advanced Reconstruction Toolbox (BART) toolbox.6
Figure 1.

(A) Sampling mask for 4x acceleration, (B) Fully sampled image, (C) Undersampled constrained reconstruction with no TV regularization, (D) 4x undersampled constrained reconstruction with TV regularization parameter TV = 10−2.Aliasing in the vertical axis is visible in the undersampled images. There are slightly fewer artifacts and slightly more blurring in the reconstruction with TV regularization.
2.2. Constrained reconstruction from multi-coil data
Constrained reconstruction minimizes a data agreement functional with additional constraints. For this work we consider a total variation constraint4 and multi-coil data with the coil sensitivities estimated using the sum of squares method which leads to real estimates of the underlying object.
2.3. Two-alternative forced choice experiments
In each individual trial of the 2AFC experiment we presented three 128×128 pixel images: one image of an anatomical background with the signal, the signal, and one image of an anatomical background without the signal. The signal image was always in the center, and the location (left or right) of the anatomical image with the signal was randomly chosen for each trial. An example trial is shown in Figure 2. The signal location is always in the middle of the anatomical image, which makes this task a signal known exactly (SKE) and the human observer only determines whether or not it is present in the image.
Figure 2.

Sample 2AFC trial with signal in the left image.
2.4. Experimental procedure
For each experimental condition, 200 2AFC trials were carried out by three observers. As training, all observers repeated an initial set of 200 trials until the performance plateaued. Based on performance in the training trials, the signal amplitude was chosen so that the mean percent correct for the observers would be close to 80 percent.
Because of the physical distancing required due to COVID-19, the experiment locations and conditions of each observer differed. Two of the observers (1 and 3) used their laptops (MacBook Air and MacBook Pro) and observer number 2 used a Barco MDRC 2321 monitor. Each observer took the studies in a dark room. The resolution of the laptops was set so that the pixel pitch was 0.28 mm and the resolution of the Barco monitor was 0.294 mm. All observers were approximately 50 cm from the screen.
For each individual trial, a set of images like Figure 2 appeared on the screen and the observer chose which image they believed contained the signal. The answers for each trial are recorded, as well as the time in between each trial, the location of coordinates that the user clicked, and which specific images in the set were chosen correctly or incorrectly. The observers received feedback on whether they had identified the signal correctly after each trial for possible improvement between trials and took breaks between sets of 200 trials to avoid fatigue.
2.5. Model observers
We used the non-prewhitening eye (NPWE) observer7 and the channelized Hotelling observer with sparse difference-of-Gaussians (S-DOG) channels8 to model human observer performance in the 2-AFC experiments as we varied the regularization parameter in the TV constraint.
The NPWE applies a template that does not whiten the background noise of an image, but models the human eye response to frequencies in an image. Based on these frequencies and mathematical responses, a decision of which image contains the signal is made. The eye filter that was used in this study is of the form
where f is the distance from the zero frequency, we chose c for the eye filter to peak at 5 cycles per degree for our images and n = 0.9 to fit the experimental data (Figure 3).
Figure 3.
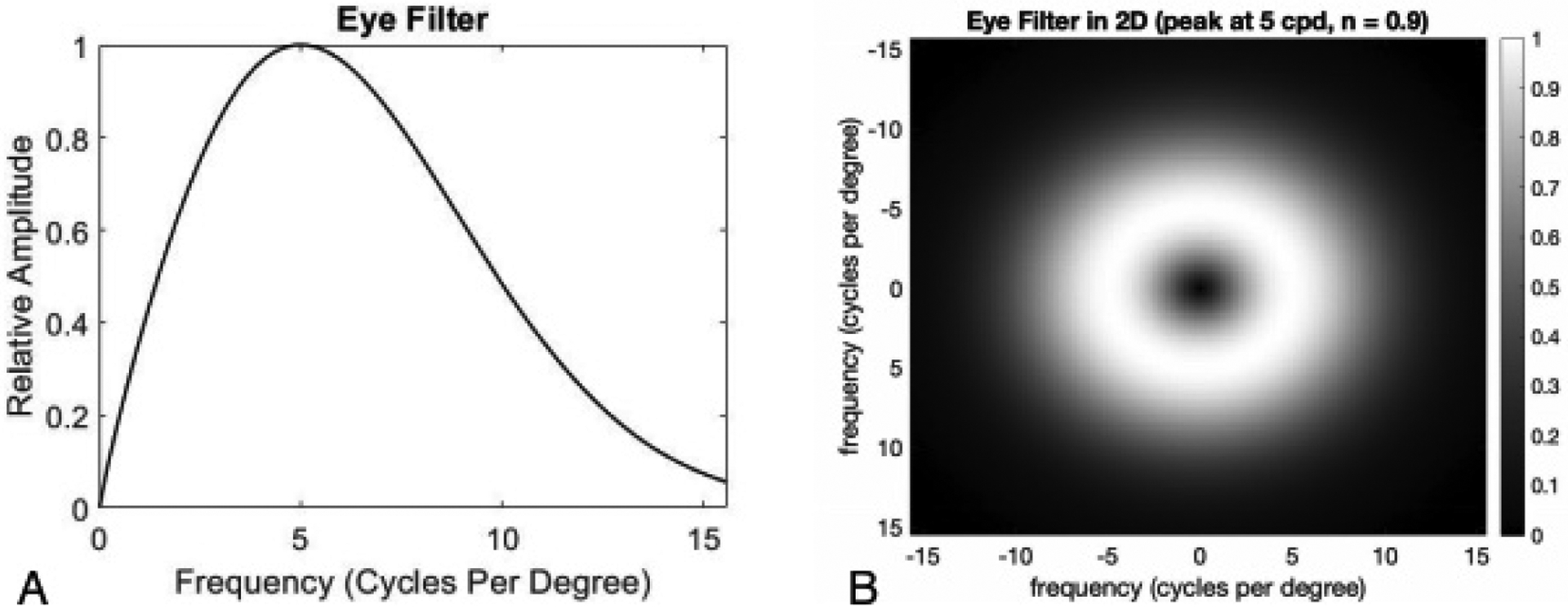
(A) A cross section of the eye filter matched for human performance with TV = 0. (B) The 2-dimensional eye filter matched for human performance with no TV regularization.
The second model that we used in our study was the S-DOG channelized Hotelling Observer. The S-DOG channels whiten the noise within the images by using the inverse covariance matrix and applying the template.8 We used the S-DOG of the form
where f is the distance from the zero frequency, Q is the multiplicative factor of the bandwidth,
where j denotes the jth channel and σj denotes the standard deviation of each channel. The parameters that were used for the S-DOG were Q = 2, α = 2, and σ0 = 0.015 which were used by Abbey8 (Figures 4, 5). In order to match the high performing S-DOG observer to our human data, it was necessary to add internal noise. We used an internal noise model that added uncorrelated normal noise to the channel outputs for each image.8
Figure 4.

(A) The cross section of S-DOG channels matched for human performance with no TV regularization in the frequency domain and (B) spatial domain.
Figure 5.

A, C, and E are the basis images for the S-DOG channels in the spatial domain, B, D, and F are the basis images in the frequency domain. The zero frequency is empty because the human eye is unable to see the zero frequency.
3. RESULTS AND DISCUSSION
We utilized four sets of FLAIR images that were generated with 4x acceleration and at four different values of TV regularization: 0, 0.001, 0.01, and 0.1. The signal amplitude was chosen to achieve a percent correct for humans of about 0.8 for no regularization.
The NPWE observer was matched to human performance for TV = 0 with a peak of 5 cycles per degree and n = 0.7. As seen in Figure 6, this observer was matched exactly at TV = 0 but also captures the performance of the average human observer for both TV = 0.001 and 0.01. At the largest regularization value of TV = 0.1, the NPWE slightly overestimated the performance of the human observers. The eye filter that was used for matching this data can be seen in Figure 3.
Figure 6.

NPWE observer matched to human observer for images with no TV regularization. The NPWE observer tracked the human observer data for the other regularization parameters with a slight overestimate for a large amount of regularization.
Unlike the NPWE which was chosen to match the average human performance, the S-DOG alone highly overestimated human performance without the addition of noise. However, the pattern of performance as TV increased was the same as both the human observers and the NPWE model observer. Once the internal noise was added, a similar trend of tracking the human performance to the NPWE can be seen with the S-DOG in Figure 7. For all levels of TV = 0, 0.001, 0.01, and 0.1, the S-DOG closely tracks human performance.
Figure 7.
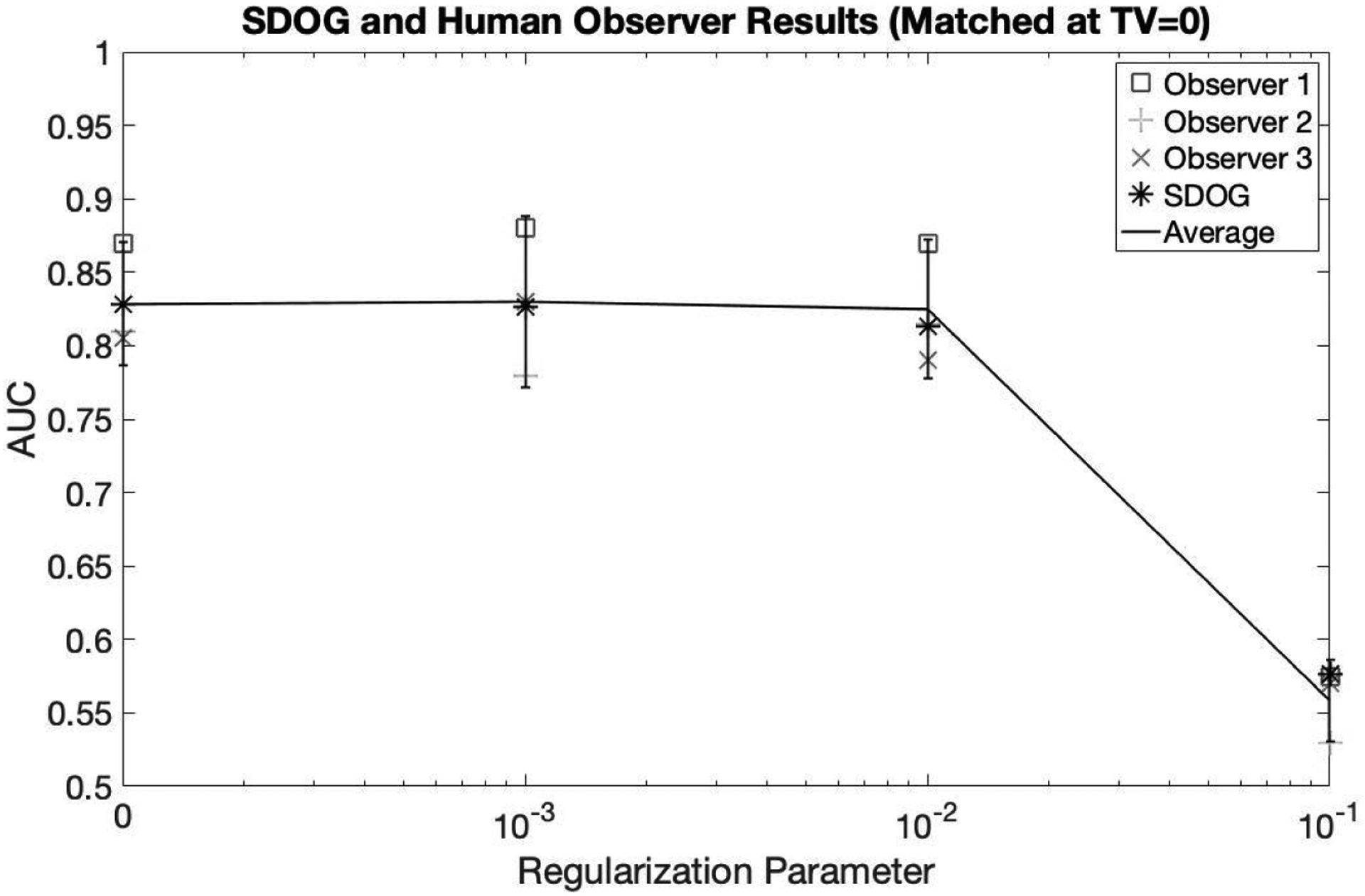
S-DOG observer with internal noise matched to human observer for images with no TV regularization. The S-DOG observer tracked the human observer data for the other regularization parameters.
Both the NPWE and S-DOG with internal noise were able to track human performance for image sets as regularization parameter changes. Additionally, our results suggest that TV constraint does not improve human detection performance for this task.
4. CONCLUSION
To our knowledge, this is the first application of model observers for tracking human observer detection performance in undersampled MRI. Both model observers followed the same pattern as the average performance of the human observers. However, the S-DOG was able to track human performance at all levels of regularization, but the NPWE slightly overestimated human performance at large amounts of regularization. One of the results of this study is that model observers are able to track human observer performance as the regularization changes. The other result is that the TV constraint does not improve human detection performance for this task.
ACKNOWLEDGMENTS
This work was supported by the National Institute of Biomedical Imaging and Bioengineering of the National Institute of Health under award number R15-EB029172. The authors thank Dr. Krishna S. Nayak at the University of Southern California and Dr. Craig K. Abbey at University of California, Santa Barbara for their time and guidance.
REFERENCES
- [1].Barrett HH, “Objective assessment of image quality: effects of quantum noise and object variability,” J. Opt. Soc. Am. A 7, 1266–1278 (Jul 1990). [DOI] [PubMed] [Google Scholar]
- [2].Barrett HH and Myers KJ, [Foundations of Image Science], John Wiley and Sons, Hoboken NJ (2004). [Google Scholar]
- [3].Wang Z, Bovik A, Sheikh H, and Simoncelli E, “Image quality assessment: From error visibility to structural similarity,” IEEE Trans. Image Process 13, 600–612 (2004). [DOI] [PubMed] [Google Scholar]
- [4].Lustig M, Donoho D, and Pauly JM, “Sparse mri: The application of compressed sensing for rapid mr imaging,” Magn. Reson. Med 58, 1182–1195 (2007). [DOI] [PubMed] [Google Scholar]
- [5].Knoll F and Zbontar J, “fastmri: A publicly available raw k-space and dicom dataset of knee images for accelerated mr image reconstruction using machine learning,” Radiology: Artificial Intelligence 2(1) (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Uecker M, Ong F, Tamir JI, Bahri D, Virtue P, Cheng JY, Zhang T, and Lustig M, “Berkeley advanced reconstruction toolbox,” Proc. Intl. Soc. Mag. Reson. Med 23, 2486 (2015). [Google Scholar]
- [7].Burgess AE, “Statistically defined backgrounds: performance of a modified nonprewhitening observer model,” Journal of the Optical Society of America A 11(4), 1237–1242 (1994). [DOI] [PubMed] [Google Scholar]
- [8].Abbey CK and Barrett HH, “Human and model-observer performance in ramp-spectrum noise: effects of regularization and object variability,” Journal of the Optical Society of America A 18(3), 473–488 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]


