Abstract
Objectives
The ability to identify novel risk factors for health outcomes is a key strength of electronic health record (EHR)-based research. However, the validity of such studies is limited by error in EHR-derived phenotypes. The objective of this study was to develop a novel procedure for reducing bias in estimated associations between risk factors and phenotypes in EHR data.
Materials and Methods
The proposed method combines the strengths of a gold-standard phenotype obtained through manual chart review for a small validation set of patients and an automatically-derived phenotype that is available for all patients but is potentially error-prone (hereafter referred to as the algorithm-derived phenotype). An augmented estimator of associations is obtained by optimally combining these 2 phenotypes. We conducted simulation studies to evaluate the performance of the augmented estimator and conducted an analysis of risk factors for second breast cancer events using data on a cohort from Kaiser Permanente Washington.
Results
The proposed method was shown to reduce bias relative to an estimator using only the algorithm-derived phenotype and reduce variance compared to an estimator using only the validation data.
Discussion
Our simulation studies and real data application demonstrate that, compared to the estimator using validation data only, the augmented estimator has lower variance (ie, higher statistical efficiency). Compared to the estimator using error-prone EHR-derived phenotypes, the augmented estimator has smaller bias.
Conclusions
The proposed estimator can effectively combine an error-prone phenotype with gold-standard data from a limited chart review in order to improve analyses of risk factors using EHR data.
Keywords: association study, bias reduction, differential misclassification, electronic health records, error in phenotype
INTRODUCTION
Electronic health records (EHRs) contain extensive patient data, providing an efficient and wide-reaching source for health research.1,2 In the last decade, EHR data have been widely used to investigate research questions in various health care and medical domains. In Figure 1, we present a commonly used standardization process for EHR data. This figure demonstrates the flow from data in a medical data warehouse to data ready for research analysis. One common use of EHR data is identification of novel risk factors for disease, referred to as an association study.3
Figure 1.
An illustration of the pipeline for preparing EHR data for research use. To conduct association studies, health outcomes are typically derived from a phenotyping algorithm. Algorithms with different characteristics (eg, algorithm specific characteristics, patient-level characteristics) lead to phenotypes of different qualities (ie, different sensitivity and specificity) for use in the subsequent association study. Following the phenotyping process, manual chart reviews are often conducted to provide gold-standard phenotypes. The proposed method is a novel method in the downstream analyses to account for phenotyping error.
However, such EHR-based association studies face many challenges. One major challenge is measurement error in EHR-derived outcomes.4 For example, the binary phenotypes of patients in EHR data are derived through phenotyping algorithms (Figure 1). The performance of these algorithms, which highly depend on the types of diseases and qualities of algorithms, are rarely perfect resulting in misclassification. Errors in EHR-derived phenotypes can lead to systematic bias, substantially inflate type I error, and diminish statistical power.5–18 An existing method proposed by Sinnott et al (2014) incorporates the algorithm-derived probability of disease status into analyses using EHR-derived phenotypes. This method improves the power of association tests with imperfect phenotypes from the EHR.19
An alternative to relying on an algorithm-derived phenotype, which may suffer from misclassification, is to conduct validation through manual chart review (Figure 1) and use these validated phenotypes for association studies; for example, Ritchie et al,3 Ritchie et al,20 and Bush et al.21 Although chart reviews have the potential to provide gold-standard phenotypes, they are typically expensive and therefore usually conducted only for a small subset of patients. However, because of the small validation set, this estimator in subsequent association studies is often not efficient (ie, the estimator has large variance).
Another method developed by Magder and Hughes (1997), less commonly used in EHR-based association studies than in conventional epidemiological studies, postulates a misclassification model for the relationship between misclassification rates (ie, sensitivity and specificity) and exposure levels and correct association estimates using the estimated misclassification rates from the validation set.22,23 Nevertheless, this method relies on the correctly specified misclassification model and availability of a relatively large validation sample to ensure unbiased and efficient estimates of the parameters. McInturff et al (2004) developed a Bayesian method that incorporates information on the prior distribution of sensitivity and specificity.24 However, this method assumes that the misclassification of disease state is non-differential with respect to covariates. If sensitivity or specificity of the phenotyping algorithm varies across exposure groups, exposure-specific sensitivity and specificity estimates are required. To handle differential misclassification, Lyles et al (2011) extended Magder and Hughes’ maximum likelihood estimation method by modeling the dependence of the misclassification rates on covariates through regression models.25 Edward et al (2013) developed a multiple imputation method to account for misclassification when validation data are available.26 However, these 2 approaches require a correctly specified misclassification rate model. For EHR data, the performance of a phenotyping algorithm depends on a variety of factors, including missing data patterns, types of risk predictors, and phenotyping models. Correct specification of the misclassification rate of a phenotyping algorithm may be challenging.
In this article, we propose a method to reduce bias in EHR-based studies using the algorithm-derived phenotype with available validation data for a small subset of the population. The key idea is motivated by Wang and Wang (2015)27 who considered measurement errors in covariates when modeling time-to-event outcomes and proposed a marginal bias correction method without modeling the misclassification. By deriving the joint distribution of 2 sets of marginal estimators, an augmented estimator of associations is obtained using the conditional normal distribution. In this article, we consider binary phenotypes and propose a novel augmented estimator with better statistical properties. The proposed method utilizes the biased estimator from error-prone phenotypes to improve the statistical efficiency of the estimator from validation data only. This strategy obviates the need to model the dependency of misclassification rates on exposure levels, making it particularly useful in EHR-based research. The goal of the proposed method is to combine the strengths of the estimates using validation data only (ie, low bias) with estimates using algorithm-derived phenotype (ie, smaller variance). Through simulation studies and real data analysis, we demonstrate that the proposed method has consistently better statistical properties under a wide spectrum of misclassification settings.
MATERIALS AND METHODS
Data structure and notation
We considered an EHR-derived data set of N patients to conduct an association study between a binary phenotype, Y, and a set of covariates, X. Instead of the true phenotype, Y, the EHR data contain an algorithm-derived phenotype, S, derived from an automated algorithm which is subject to misclassification. A validation set of n subjects is randomly sampled, and the true phenotype, Y, is obtained in this sub-sample. The ratio of the validation set size to the full data set size (ie, the validation ratio) is
Figure 2.
Illustration of data structure of the BRAVA study. The first column shows the true second cancer breast event (SBCE) status obtained through chart review in validation data. The data is often available for a small subset of patients (size = n). The second column is the SBCE status from an automated algorithm, which is subject to misclassification (size = N). The last 4 columns represent the set of risk factors (ie, year, age, stage, and ER_PR [Surveillance, Epidemiology, and End Results (SEER), estrogen receptor (ER), and progesterone receptor (PR) status of index breast cancer]), which are available for all subjects in the EHR data.
Existing methods
Model (1): validation data only
The association between the covariates and true phenotype is estimated using
Model (2): naïve approach
The association is estimated using S in the full sample through a logistic regression model. The resultant estimator, denoted
Model (3): misclassification-adjusted approach
The validation set can be used to estimate sensitivity and specificity. These estimates are used to calibrate the parameter of interest,
Proposed Method
Model (4): the augmented estimator
The key idea of the proposed method is to combine the advantages of the estimators in models (1) and (2) through the joint distribution of the 2 estimators without explicitly specifying the misclassification model. This procedure outperforms model (3) in the case of incorrect misclassification models. In practical situations, the true value of
This derivation suggests an augmented estimator as follows,
| (1) |
where
Intuitively, we consider that all estimates are scalers (ie, 1-dimensional). In extreme cases where the surrogate S is noninformative and completely random, the proposed estimate of the covariance between
Algorithm
The algorithm of the augmented estimation procedure is outlined in the following algorithm and illustrated in Figure 3:
Figure 3.
An illustration of the algorithm of computing the proposed augmented estimator. Step I, use the gold standard outcome, Y, in validation data to obtain
Algorithm:
Obtain
Obtain
Obtain
Obtain the proposed estimator
Simulation studies and data evaluation
To evaluate the empirical performance of our proposed method, we use simulation studies under different misclassification settings and compare the bias and efficiency of the proposed augmented estimator with other estimators. We consider both nondifferential and differential misclassifications. Nondifferential misclassification assumes a constant error rate across exposure levels while differential misclassification assumes different error rates across subjects and may be dependent on exposure levels. In Table 1, we present the comparisons between 4 models.
Table 1.
List of models compared in the simulation studies
| Models compared | Data and model used | Pros | Cons |
|---|---|---|---|
| Model (1) | Validation data and gold standard outcome | Small bias | High variance |
| Model (2) | Full EHR data and algorithm-derived phenotype | Small variance | Often high bias |
| Model (3) | Full EHR data and algorithm-derived phenotype with correction for misclassification | Small bias and variance with correctly specified misclassification | Potential for high bias with incorrectly specified misclassification |
| Model (4) | Combined validation and full EHR with algorithm-derived phenotype | Small bias and small variance | Potential for bias with small validation set |
Simulation settings
In simulation studies, the choice of input values is motivated by distributions observed in the second breast cancer events data. Starting from these values, we select additional values to cover the expected range in real EHR studies. We assume the full data set size is N = 5000, and investigate validation sets of 4 sizes: n = 100, 200, 400, and 800 (ie, the corresponding values of
Figure 4.
Values of specificity (P) and sensitivity (S) under non-differential (left panel) and differential misclassification (right 2 panels) settings.
Under the nondifferential scenario (ie, scenario 0), the values of sensitivity and specificity were not dependent on the exposure level. We set the values to 0.90 and 0.95, respectively. Under the differential scenarios (ie, scenarios 1 and 2), the values of sensitivity and specificity differed between exposure groups. In the nonexposed group (X = 0), the values were the same as in scenario 0. In the exposed group (X = 1), because of the tradeoff between sensitivity and specificity,29 we assumed higher sensitivity and lower specificity in scenario 1; lower sensitivity and higher specificity in scenario 2 (Figure 4). The values for sensitivity (0.90) and specificity (0.95) investigated were motivated by the performance of the breast cancer phenotyping algorithm developed for the data in our motivating example. We have conducted additional simulation studies for other values of sensitivity and specificity (eg, 0.85 and 0.90, and a much lower setting 0.60 and 0.80). Based on the values of disease prevalence, sensitivity, and specificity, the range of corresponding positive predictive values (PPV) is from 31% to 92%, which covers the full spectrum of algorithm performance likely to be encountered in research practice. The relative performance of the proposed method, compared to the existing ones, was consistent with our previous investigation with a wide range of PPV. The details on the additional simulation studies are found in Supplementary Appendices 4 and 5.
Each simulation scenario was repeated 100 times. We estimated the bias of each estimator by taking the difference between the estimated value and the true value and averaging across all simulations. Standard errors were computed as the mean of the standard errors for each estimator averaged across all simulations. R code to implement the proposed method with sample simulated data is available on GitHub (https://github.com/Penncil/EHR-based-Study) and our group website (https://www.penncil.org/software).
Results
In Figure 5, we present boxplots of simulation results for scenarios 0, 1, and 2.
Figure 5.
Comparisons of simulation results of 4 models (1)–(4) under 3 scenarios, where scenario 0 is the nondifferential misclassification setting, and the other 2 are differential misclassification settings. Each notched box in the plots represents 1 model. The solid black segment in each box shows the median of the estimates and the boundaries of the colored boxes give the interquartile ranges for the estimates. The y-axis is the value of the estimated log odds ratio and the dotted horizontal line is the true value of
The red boxes on the left, representing the method using validation data only (ie, model (1)), give unbiased but inefficient estimates. The widths of the boxes are large, which means the variances of the estimates are large due to the small observed validation set. The orange boxes represent estimates using the algorithm-derived phenotype outcome in the full EHR data set (ie, model (2)). Since the algorithm-derived phenotype suffers from misclassification, the estimator is biased compared to the true value of
In Figure 6, we present comparisons for bias and standard errors across alternative models under differential misclassification scenario 1. The purple line is generated by the proposed model (4). The black horizontal line in each bias plot at zero is provided for reference. In the plots presenting estimated bias, model (4) (purple) has less bias than model (2) (orange) and model (3) (blue). In plots comparing the value of standard error, model (4) has fewer standard errors than model (1) (red). The proposed method combines the advantage of model (1) and model (2); in addition, model (4) performed consistently well under both nondifferential and differential misclassification settings compared to model (3). Results under scenario 0 and 2 with N = 5000 and additional simulation studies for smaller (N = 3000) and larger (N = 10 000) sizes of full data are provided in Appendix 3. More simulations on comparison of the proposed method with Lyles et al’s (2014) and Edwards et al’s (2013) method are provided in Supplementary Appendix 6.
Figure 6.
Comparisons of bias (left panels) and standard error (right panels) of 4 estimators from models (1)–(4) under differential misclassification scenario 1 for validation sample sizes (n = 100, upper panels, and n = 400, lower panels) and true regression parameter values. Y-axis in left panels represents the bias between estimates obtained from each model and true value of association parameter
Data evaluation
To illustrate the proposed method, we analyzed data from the BRAVA study, an investigation of risk factors for second primary or recurrent breast cancers (jointly termed second breast cancer events [SBCE]) in women with a personal history of breast cancer.30 The study included 3152 women enrolled in Kaiser Permanente Washington (KPWA), a large integrated health care system in Washington state, diagnosed with a primary stage I–IIB invasive breast cancer between 1993 and 2006. Patient demographics and primary breast cancer characteristics were available from the KPWA virtual data warehouse. Because cancer recurrence is imperfectly captured in administrative data, a medical records review was conducted for all women to ascertain a gold standard SBCE phenotype. Additionally, algorithms for identifying SBCE using administrative and cancer registry data were developed.31 The BRAVA data thus provide both a gold standard and phenotype algorithm classified SBCE phenotype for all women. We used these data to compare the magnitude and variance of estimates for the association of age at primary cancer diagnosis and primary breast cancer stage with occurrence of SBCE on a single model based on 4 models when subsets of the data were sampled and treated as a validation subset.
We investigated performance of the 4 models using 3 different EHR-derived imperfect phenotypes. First, we used the “high specificity” imperfect phenotype developed by the BRAVA study.31 The sensitivity and specificity of this algorithm were 89% and 99%, respectively. Second, we generated an imperfect phenotype with known nondifferential sensitivity of 0.9 and specificity of 0.95 by simulating the imperfect phenotype from a Bernoulli distribution with probability 0.9 for true cases and 0.05 for true noncases. Finally, we generated an imperfect phenotype with known differential misclassification. For patients with stage 1 disease, we simulated the imperfect phenotype with sensitivity and specificity of 0.9 and 0.95, respectively. For patients with stage 2 disease, we simulated the imperfect phenotype with sensitivity 0.95 and specificity 0.9. This reflects the situation that might result if a patient with a more advanced primary cancer diagnosis interacts more frequently with the health care system resulting in a lower probability of a missed SBCE (higher sensitivity) as well as higher probability of being erroneously classified as having SBCE when no second cancer has occurred (lower specificity).
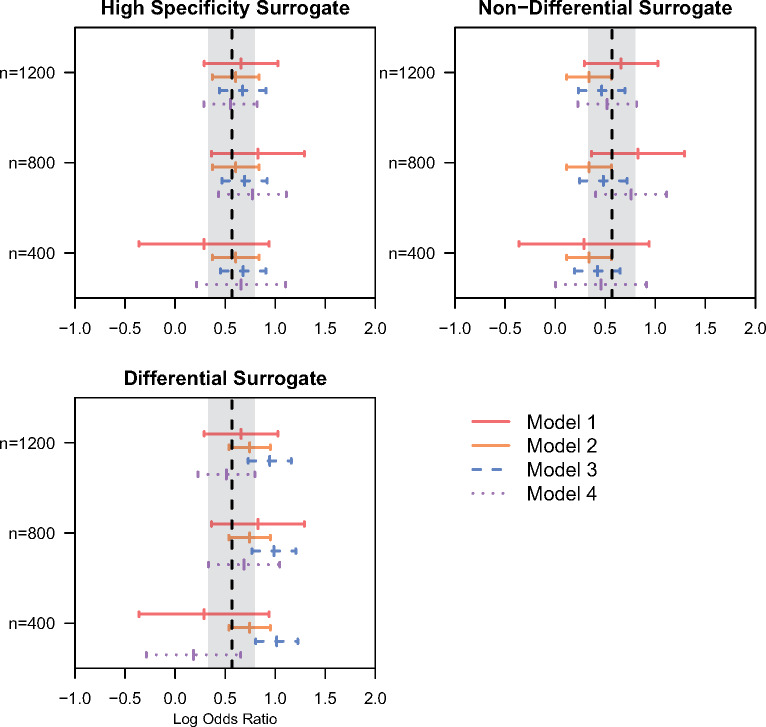
Of the 3152 patients included in the data set, 407 (12.9%) experience an SBCE. The median age of patients at diagnosis of their primary breast cancer was 63 years (interquartile range 52–73). The majority of patients (78.6%) had Stage 1 disease at diagnosis. Figure 7 presents results of 3 models applied to the BRAVA data as well as an estimate based on the gold standard outcome estimated in the full sample (vertical dashed line). For validation samples of sizes 800 and 1200, the proposed approach ((model (4), purple dashed line) provides a similar estimate to that based on the gold standard in the full sample while substantially reducing uncertainty relative to an estimate based on the validation data only (model (1), red solid line). This result was consistent across all 3 imperfect phenotypes investigated. When a validation sample size of 400 was used, the proposed estimator was somewhat more unstable and sometimes exhibited bias relative to the full data estimate. When using the high specificity imperfect phenotype, the estimate based on the full sample (model (2), orange solid line) returned an estimate very similar to the gold standard applied in the full sample. For the simulated nondifferential and differential imperfect phenotypes the full data estimate was notably biased. The plug-in estimator (model (3), blue dashed line) had low bias relative to the estimate based on the gold standard in the full sample when using the high specificity imperfect phenotype and the simulated non-differential imperfect phenotype. For the imperfect phenotype with differential misclassification, association estimates for stage based on the plug-in estimator were upwardly biased.
Figure 7.
Point estimates and 95% confidence intervals (CI) for the association (in log odds ratio scale) between the primary breast cancer stage and the occurrence of second breast cancer events (SBCE) using the data from the BRAVA study, where validation sample size was n = 400, 800, or 1200. The vertical dashed line represents the point estimate of the association based on the gold standard SBCE status estimated from the full sample (N = 3152) and grey bands provide a 95% CI for the association estimate. The estimates of association for age are presented in Supplementary Appendix 7.
DISCUSSION
Phenotype misclassification is a major challenge to association estimation using EHR data. Either nondifferential or differential outcome misclassification can negatively influence statistical efficiency and lead to bias. One current approach is to restrict association analyses to a validation set where the gold standard phenotype has been ascertained. However, the small validation set leads to large variance of this estimator. Another approach is to ignore the potential misclassification. This method leads to bias, although variance is small due to the large full data set. In this article, we proposed an estimation procedure to integrate the strengths of the above 2 estimators, and created an augmented estimator which has small bias and high efficiency (ie, small variance) simultaneously. The proposed method uses the validation data and the EHR-derived phenotypes together to reduce the effects of misclassification, and does not require explicitly modeling sensitivity and specificity. Under the nondifferential misclassification setting, the performance of Magder and Hughes’ method is similar to that of the augmented estimator. However, in reality, it is difficult to know whether misclassification is differential or nondifferential. We therefore believe the proposed approach is preferable because it maintains good performance regardless of whether misclassification is differential. By handling the complexity of misclassification nonparametrically, this novel estimation procedure is a robust approach to phenotype misclassification in EHR-based association studies. Since ignoring or inappropriate handling of error in EHR-derived data will lead to inflated type I error and loss of power,6,18,32 the proposed method enhances the reproducibility of EHR-based clinical findings by lowering both type I and type II error, contributing to the improved validity of research findings in clinical practice.
We note that the validity of the augmented estimator is robust to the misspecification of model (2) on the relation between the imperfect outcome and the risk factors. On the other hand, specifying a regression model that is close to the true relationship between the imperfect outcome and the risk factors can lead to better statistical efficiency of the proposed estimator. To achieve a more flexible working model, we can include more risk factors in the prediction of the algorithm-derived outcome. In other words, we formulated the case where the set of risk factors for the algorithm-derived outcome is the same as the risk factors for the true disease status. However, this assumption can be relaxed. The additional benefit of specifying a larger set of risk factors for the imperfect outcome, in terms of efficiency gain, will be investigated in the future.
The proposed method has a few limitations. First, bias may be introduced when the validation set is small, as observed in our analysis of BRAVA data. This is because the augmented estimator is obtained conditionally on the observed value of
There are a few extensions for future investigations. First, our method is suitable for data augmentation with moderate or relatively high disease prevalence, such as type 2 diabetes. For relatively rare diseases, random sampling of patients for chart review is suboptimal, because the number of true cases in the validation data will be small, leading to increased bias and low efficiency of the estimate
CONCLUSION
Association analyses of EHR data that ignore misclassification in EHR-derived phenotypes have the potential for substantial bias. Concerningly, given the typically large samples encountered in such studies, these biased results may be estimated with high precision, creating a high risk of erroneous inference. Our proposed approach provides a means to reduce bias while maintaining low variance that is straightforward to implement using standard statistical software.
FUNDING
This work is supported in part by the National Institutes of Health grants 1R01LM012607, 1R01AI130460, P50MH113840, 1R01AI116794, R01LM009012, R01HD099348 and R01LM010098, and the Patient-Centered Outcomes Research Institute (PCORI) under award number ME-1511-32666. All statements in this report, including its findings and conclusions, are solely those of the authors and do not necessarily represent the views of NIH, PCORI, the PCORI Board of Governors, or the PCORI Methodology Committee.
AUTHOR CONTRIBUTIONS
JT, JH, RH, and YC designed the methods and experiments; JC and RH provided the data set from Kaiser Permanente Washington for data analysis; JH, RH, and YC guided the data set generation for the simulation study; JT generated the simulation data sets, conducted simulation experiments, and conducted data analysis of the EHR data from Kaiser Permanente Washington; JT, JH, JC, XW, JM, RH, and YC interpreted the results and provided instructive comments; JT, JH, RH, and YC drafted the main manuscript. All authors have approved the manuscript.
Supplementary Material
ACKNOWLEDGMENTS
We wish to thank Zixuan Liu for helpful discussion on the data analysis.
Conflict of Interest statement
None declared.
REFERENCES
- 1. Jensen PB, Jensen LJ, Brunak S.. Mining electronic health records: towards better research applications and clinical care. Nat Rev Genet 2012; 13 (6): 395–405. [DOI] [PubMed] [Google Scholar]
- 2. Hripcsak G, Albers DJ.. Next-generation phenotyping of electronic health records. J Am Med Inform Assoc 2013; 20 (1): 117–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Ritchie MD, Denny JC, Crawford DC, et al. Robust replication of genotype-phenotype associations across multiple diseases in an electronic medical record. Am J Hum Genet 2010; 86 (4): 560–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Haneuse S, Daniels M.. A general framework for considering selection bias in EHR-based studies: what data are observed and why? EGEMS (Wash DC) 2016; 4: 1203.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Neuhaus JM. Bias and efficiency loss due to misclassified responses in binary regression. Biometrika 1999; 86 (4): 843–55. [Google Scholar]
- 6. Duan R, Cao M, Wu Y, et al. An empirical study for impacts of measurement errors on EHR based association studies. AMIA Annu Symp Proc 2016; 2016: 1764–73. [PMC free article] [PubMed] [Google Scholar]
- 7. Barron BA. The effects of misclassification on the estimation of relative risk. Biometrics 1977; 33 (2): 414–8. [PubMed] [Google Scholar]
- 8. Copeland KT, Checkoway H, McMichael AJ, et al. Bias due to misclassification in the estimation of relative risk. Am J Epidemiol 1977; 105 (5): 488–95. [DOI] [PubMed] [Google Scholar]
- 9. Greenland S. Variance estimation for epidemiologic effect estimates under misclassification. Stat Med 1988; 7 (7): 745–57. [DOI] [PubMed] [Google Scholar]
- 10. Liu XH, Liang KY.. Adjustment for non-differential misclassification error in the generalized linear model. Stat Med 1991; 10 (8): 1197–211. [DOI] [PubMed] [Google Scholar]
- 11. Morrissey MJ, Spiegelman D.. Matrix methods for estimating odds ratios with misclassified exposure data: extensions and comparisons. Biometrics 1999; 55 (2): 338–44. [DOI] [PubMed] [Google Scholar]
- 12. Rekaya R, Weigel KA, Gianola D.. Threshold model for misclassified binary responses with applications to animal breeding. Biometrics 2001; 57 (4): 1123–9. [DOI] [PubMed] [Google Scholar]
- 13. Lyles RH. A note on estimating crude odds ratios in case-control studies with differentially misclassified exposure. Biometrics 2002; 58 (4): 1034–6; discussion 1036–7. [DOI] [PubMed] [Google Scholar]
- 14. Paulino CD, Soares P, Neuhaus J.. Binomial regression with misclassification. Biometrics 2003; 59 (3): 670–5. [DOI] [PubMed] [Google Scholar]
- 15. Luan X, Pan W, Gerberich SG, et al. Does it always help to adjust for misclassification of a binary outcome in logistic regression? Stat Med 2005; 24 (14): 2221–34. [DOI] [PubMed] [Google Scholar]
- 16. Greenland S. Maximum-likelihood and closed-form estimators of epidemiologic measures under misclassification. J Stat Plan Inference 2008; 138 (2): 528–38. [Google Scholar]
- 17. Lyles RH, Lin J.. Sensitivity analysis for misclassification in logistic regression via likelihood methods and predictive value weighting. Stat Med 2010; 29 (22): 2297–309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Chen Y, Wang J, Chubak J, et al. Inflation of type I error rates due to differential misclassification in EHR-derived outcomes: empirical illustration using breast cancer recurrence. Pharmacoepidemiol Drug Saf 2019; 28 (2): 264–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Sinnott JA, Dai W, Liao KP, et al. Improving the power of genetic association tests with imperfect phenotype derived from electronic medical records. Hum Genet 2014; 133 (11): 1369–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Ritchie MD, Holzinger ER, Li R, et al. Methods of integrating data to uncover genotype-phenotype interactions. Nat Rev Genet 2015; 16 (2): 85–97. [DOI] [PubMed] [Google Scholar]
- 21. Bush WS, Oetjens MT, Crawford DC.. Unravelling the human genome-phenome relationship using phenome-wide association studies. Nat Rev Genet 2016; 17 (3): 129–45. [DOI] [PubMed] [Google Scholar]
- 22. Magder LS, Hughes JP.. Logistic regression when the outcome is measured with uncertainty. Am J Epidemiol 1997; 146 (2): 195–203. [DOI] [PubMed] [Google Scholar]
- 23. Chen Z, Yi GY, Wu C.. Marginal methods for correlated binary data with misclassified responses. Biometrika 2011; 98 (3): 647–62. [Google Scholar]
- 24. McInturff P, Johnson WO, Cowling D, et al. Modelling risk when binary outcomes are subject to error. Stat Med 2004; 23 (7): 1095–109. [DOI] [PubMed] [Google Scholar]
- 25. Lyles RH, Tang L, Superak HM, et al. Validation data-based adjustments for outcome misclassification in logistic regression: an illustration. Epidemiology 2011; 22 (4): 589–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Edwards JK, Cole SR, Troester MA, et al. Accounting for misclassified outcomes in binary regression models using multiple imputation with internal validation data. Am J Epidemiol 2013; 177 (9): 904–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Wang X, Wang Q.. Semiparametric linear transformation model with differential measurement error and validation sampling. J Multivar Anal 2015; 141: 67–80. [Google Scholar]
- 28. Carroll RJ, Ruppert D, Crainiceanu CM, et al. Measurement Error in Nonlinear Models: A Modern Perspective. Boca Raton, FL: Chapman and Hall/CRC; 2006. pp.32. [Google Scholar]
- 29. Chubak J, Pocobelli G, Weiss NS.. Tradeoffs between accuracy measures for electronic health care data algorithms. J Clin Epidemiol 2012; 65 (3): 343–9.e2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Boudreau DM, Yu O, Chubak J, et al. Comparative safety of cardiovascular medication use and breast cancer outcomes among women with early stage breast cancer. Breast Cancer Res Treat 2014; 144 (2): 405–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Chubak J, Yu O, Pocobelli G, et al. Administrative data algorithms to identify second breast cancer events following early-stage invasive breast cancer. J Natl Cancer Inst 2012; 104 (12): 931–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Ioannidis J. Why most published research findings are false. PLoS Med 2005; 2 (8): e124.. 10.1371/journal.pmed.0020124 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Gravel CA, Platt RW.. Weighted estimation for confounded binary outcomes subject to misclassification. Stat Med 2018; 37 (3): 425–36. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.