Abstract
Motivation
Cryoelectron tomography (cryo-ET) visualizes structure and spatial organization of macromolecules and their interactions with other subcellular components inside single cells in the close-to-native state at submolecular resolution. Such information is critical for the accurate understanding of cellular processes. However, subtomogram classification remains one of the major challenges for the systematic recognition and recovery of the macromolecule structures in cryo-ET because of imaging limits and data quantity. Recently, deep learning has significantly improved the throughput and accuracy of large-scale subtomogram classification. However, often it is difficult to get enough high-quality annotated subtomogram data for supervised training due to the enormous expense of labeling. To tackle this problem, it is beneficial to utilize another already annotated dataset to assist the training process. However, due to the discrepancy of image intensity distribution between source domain and target domain, the model trained on subtomograms in source domain may perform poorly in predicting subtomogram classes in the target domain.
Results
In this article, we adapt a few shot domain adaptation method for deep learning-based cross-domain subtomogram classification. The essential idea of our method consists of two parts: (i) take full advantage of the distribution of plentiful unlabeled target domain data, and (ii) exploit the correlation between the whole source domain dataset and few labeled target domain data. Experiments conducted on simulated and real datasets show that our method achieves significant improvement on cross domain subtomogram classification compared with baseline methods.
Availability and implementation
Software is available online https://github.com/xulabs/aitom.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Plentiful complex biochemical processes and subcellular activities sustain the dynamic and complex cellular environment, in which a mass of intricate molecular ensembles participate. A comprehensive analysis of these ensembles in situ (at their original locations) inside single cells would play an essential role in understanding the molecular mechanisms of cells. Cryoelectron tomography (cryo-ET), as a revolutionary imaging technique for structural biology, enables the in situ 3D visualization of structural organization information of all subcellular components in single cells in a close-to-native state at submolecular resolution. Thus cryo-ET can bring new molecular machinery insights of various cellular processes by systematically visualizing the structure and spatial organizations of all macromolecules and their spatial interactions with all other subcellular components in single cells at unprecedented resolution and coverage.
In particular, because of fractionated total electron dose over entire tilt series (Bartesaghi et al., 2008), we need to average multiple subtomograms (subtomograms are subvolumes extracted from a tomogram, and each of them usually contains one macromolecule) that contain identical structures to get high SNR subtomogram average representing higher resolution of the underlying structure (Briggs, 2013). However, the macromolecule structures in a cell are highly diverse. Therefore, it is necessary to first accurately classify these subtomograms into subsets of structurally identical macromolecules. This is performed by subtomogram classification. Systematic structural classification of macromolecules is a vital step for the systematic analysis of cellular macromolecular structures and functions (Irobalieva et al., 2016) in many aspects including macromolecular structural recovery. However, such classification is very difficult, because of the structural complexity in cellular environment as well as the limit of data collection, such as missing wedge effects (Bartesaghi et al., 2008). Therefore, for successful automatic and systematic recognition and recovery of macromolecular structures captured by cryo-ET, it is imperative to have an efficient and accurate method for subtomogram classification.
With the technological breakthrough of cryo-ET and the development of image acquisition automation, collecting tomograms containing millions of macromolecules is no longer the obstacle for researchers, and methods based on deep learning have been proposed to address the issue of high-throughput subtomogram classification thanks to the high-throughput processing capability of deep learning. Different architectures of Convolutional Neural Network have been explored (Che et al., 2018). Despite the significant superiority in speed, accuracy, robustness and scalability compared to traditional methods, these supervised deep learning-based subtomogram classification methods often suffer from the high demand of annotated data. Currently, labeling is done by a combination of computational template search and manual inspection. However, in practice, template search is time consuming, and quality control through manual inspection is laborious. The complicated structure and distortion caused by noise make subtomogram images hard to distinguish by the naked eyes even by experts, which is a major obstacle for the manual quality insurance of the annotation.
An intuitive idea to tackle the problem of insufficient annotated data is to utilize a separated auxiliary dataset, which has abundant labeled samples, to assist subtomogram classification. Such auxiliary dataset is obtained from a separate imaging source or from simulation. Therefore, the auxiliary dataset and our target dataset have the same structural classes but different image intensity distribution. The difference can be attributed to discrepant data acquisition conditions, such as different Contrast Transfer Function, signal-to-noise ratio (SNR), resolution, backgrounds, etc. The source domain is defined as the domain that the auxiliary dataset belongs to, and the target domain is defined as the domain that the evaluation dataset belongs to. In our case, we assume that we have plenty of labeled subtomograms in the source domain, but only few labeled samples in the target domain are accessible. This is due to the difficulty to annotate the data in target domain. For example, the real cryo-ET data in the target domain acquired from cryo-ET (real dataset) might be extremely time-consuming to annotate. On the other hand, we can generate simulated cryo-ET data in the source domain on the computer as the separated auxiliary dataset to assist us to improve the prediction accuracy of the real dataset in the target domain. Unfortunately, because of the image intensity distribution discrepancy between the source domain and the target domain, a deep learning model trained on the source domain perform poorly on the target domain due to dataset shift (Quionero-Candela et al., 2009).
Domain Adaptation (Blitzer et al., 2006) is an effective way to solve this problem. This approach resolves the discrepancy of data distribution between source domain and target domain. One type of domain adaptation fine-tunes a trained neural network on source domain, which makes it perform well on both source domain and target domain. Another type of domain adaptation transforms target/source data to make it get close to the image intensity distribution of another domain (e.g. Alam et al., 2018). Therefore, neural network does not need to distinguish two domains, because their image intensity distributions are similar by properly transforming the input data. Domain adaptation can also be categorized into unsupervised and supervised approaches: Unsupervised domain adaptation (UDA) requires large amount of data but does not need target labels (e.g. Long et al., 2016), while supervised domain adaptation (SDA) requires target labels to be given (e.g. Garcia-Romero et al., 2014). Nowadays, these two methods are the mainstream methods to reduce distribution discrepancy in source domain and target domain. However, in our cryo-ET dataset, the methods based on UDA and SDA have obvious defects: (i) UDA cannot utilize the information of labeled data in target domain, therefore intraclass relationship between source domain and target domain is neglected. (ii) Often, due to annotation difficulty, there are too few labeled data in target domain that SDA cannot reach satisfactory results.
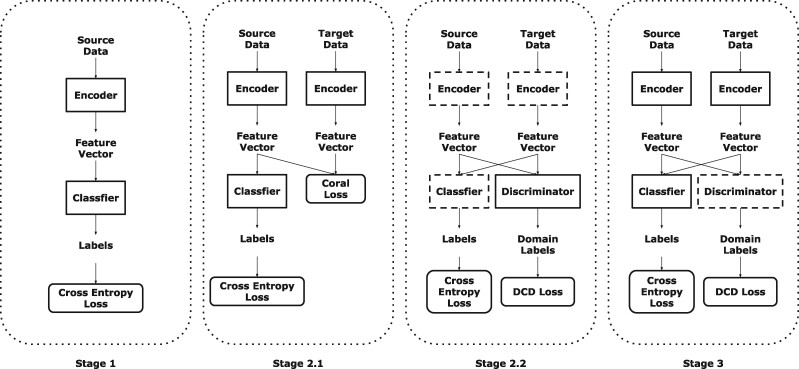
Therefore, we propose a method for Few-Shot Domain Adaptation: Few-Shot Fine-Tuning domain adaptation. Few-Shot means that each class contains only very few labels in the target domain (e.g. Motiian et al., 2017). Generally, for each class, we only use three to seven labels in the target domain. The flowchart of our method is presented on Figure 1. It contains three components: encoder , classifier g and discriminator . Encoder extracts every subtomogram into a feature vector (feature vectors represent the output of encoder ); classifier g transforms each feature vector into a one-hot label, which presents the class of each subtomogram; discriminator identifies which domain the feature vectors belong to. The detailed training procedure is explained in the following section.
Fig. 1.
The flowchart of our method. The model whose edge is imaginary line represents that its parameters are fixed. In Stage 1, an encoder and a classifier g are initially trained using data in source domain (Section 2.1). In Stage 2, a discriminator is trained to identify the domain of each subtomogram (Section 2.2). In Stage 3, labeled data in both domains are used to fine-tune the encoder with the assistance of discriminator (Section 2.3)
We have evaluated our method on both simulated and real datasets. Compared with popular baseline methods, our method achieves significantly higher classification accuracy. Additionally, related works and result analysis are presented in Supplementary Document.
Our main contributions are summarized as follows:
We are the first to use few-shot domain adaptation for cross-domain subtomogram classification.
We directly train the discriminator without adversarial training in the training procedure, comparing to FADA (Motiian et al., 2017).
We introduce a mechanism of partly shared parameters of encoder between source domain and target domain. The layers whose parameters are shared by two domains are called domain-independent layers, and the other layers are called domain-related layers (Section 2.2.1).
We combine domain discrimination for the output of independent layers and shared layers (Section 2.2.2).
2 Materials and methods
In this section, we describe our model in details. Our training strategy contains three stages. Stage 1: an encoder and a classifier g are initially trained using data in source domain (Section 2.1). Stage 2: a discriminator is trained to identify the domain of each subtomogram (Section 2.2). Stage 3: labeled data in both domains are used to fine-tune the encoder with the assistance of discriminator (Section 2.3). Stage 2.1 is UDA while Stage 2.2 and Stage 3 are SDA.
Algorithm 1 Overall algorithm
Input:
Encoder in source domain:
Encoder in target domain:
Classifier g, discriminator .
Output:
Trained , classifier g and discriminator .
1: Train and classifier g using source subtomograms (Stage 1)
2: Train and g using unlabeled target subtomograms (Stage 2.1) by algorithm 2
3: Train discriminator using labeled target and source subtomograms (Stage 2.2)
4: Fine-tune and classifier g with the assistance of discriminator and labeled target and source subtomograms (Stage 3)
2.1 Stage 1: initialize encoder and classifier g
A series of subtomogram samples in source domain are provided in this section. We apply a 3D encoder , which maps each subtomogram into a feature vector in embedding space. We introduce an embedding function to represent the encoder . Because the parameters of encoder are partly shared between source domain and target domain, the embedding function can be composited by two parts: the domain-related function or , and the domain-independent function . That is to say, we apply for source domain and for target domain.
The application of the partly shared encoder is based on the assumption that different domains have similar high-level feature (including details), because the structure of subtomograms in the same class but from different domains are similar; but their low-level features are different such as edges due to image intensity difference between domains. The front part is more for low-level features and the back part for high-level features. In other words, the front parts of encoder f0 of extract the common structural features of both domains and remove the domain-related features such as image parameters and SNR. The back parts and further extract their common feature into embedding space. Second, a classifier g maps feature vectors into one-hot labels, which is represented by a prediction function .
We update the encoders in source domain: and encoders in target domain: and classifier g by the following equation:
| (1) |
The loss function is:
| (2) |
We set n as batch size. represents the ith subtomogram image, and represents the ith subtomogram label in each subtomogram sample batch.
2.2 Stage 2: train the discriminator
After the first training step, the combination of encoders in source domain: and encoders in target domain: and classifier g have a perfect performance in classification of source domain because plentiful labeled source data is supplied. Unfortunately, due to the different experimental imaging parameters in two domains, we can hardly reach satisfactory result in target domain. Thus, the essential part of our proposed method is utilizing unlabeled data and few labeled data in target domain to improve its performance in target domain. According to our experiments, even though the amount of labeled data in target domain is scarce, they are notably conductive to the improvement of classification accuracy in test stage.
Inspired by the study by Motiian et al. (2017), we devise a discriminator for Domain Adaptation in the following stages. Motiian et al. (2017) trains the discriminator using adversarial training. The method is successful on the popular datasets such as MNIST, USPS and SVHN, because the loss function is easy to design. However, unlike the traditional 2D images, the spatial and structural information of our 3D subtomograms is very complicated and it is severely contaminated by noise. Therefore, it is difficult to train a desirable network using adversarial training because discriminator and encoders in source domain: and encoders in target domain: are very hard to converge at the same time and their performance needs to be synchronized. Thus, as much as adversarial training is able to reach a satisfactory result in the traditional image datasets which have relatively high SNR, when it comes to cryo-ET, the drawback of adversarial training would be exposed. Therefore, instead of training discriminator and encoders in source domain: and encoders in target domain: alternately like adversarial training, in our model, the discriminator is only trained once, and the parameters of the encoders and are not trained during the training of the discriminator .
In this section, we aim at training a discriminator to distinguish the domain of each feature vector, which is described in detailed below.
2.2.1. Stage 2.1: preprocessing of encoders in source domain: and encoders in target domain:
In this stage, we adjust the parameters of encoders in source domain: and encoders in target domain: . By doing this, the encoder is easier to extract the information of subtomograms of target domain. We use a discriminator to assist encoders in source domain: and encoders in target domain: to confuse two domains; on the other hand, to make the discriminator distinguish two domains well, our encoders in source domain: and encoders in target domain: must have the ability to confuse two domains. That is to say, at the beginning, the distributions of feature vectors and in the two domains should not have too much notable discrepancy. Otherwise, it would be so easy for the discriminator to identify which domain every subtomogram belongs to, and its identification ability can hardly be improved. Therefore, the training of discriminator relies on encoders in source domain: and encoders in target domain: , and the training of encoders in source domain: and encoders in target domain: relies on discriminator too. Unfortunately, neither discriminator and encoders in source domain: and encoders in target domain: are fully trained. The encoders and in two domains are all pretrained on the source data , so the parameter of the encoder in target domain is identical to the encoder in source domain. The model trained on data in source domain can hardly extract the feature in target domain very well, which becomes a major obstacle to train a discriminator .
To solve this problem, we use the following tactics. (i) Stage 2.1: apply UDA to encoders in source domain: and encoders in target domain: . (ii) Stage 2.2: train a discriminator with the help of encoders in source domain: and encoders in target domain: . (iii) Stage 3: optimize encoders in source domain: and encoders in target domain: with the help of discriminator . The detailed algorithm of Stage 2.1 is discussed as follows.
The encoder trained by source data is pre-trained in the first stage (Equation 1), which we discussed in detail in the Section 2.1. We apply UDA for encoders in source domain: and encoders in target domain: in both domains before training a discriminator . UDA utilizes unlabeled data in target domain to enable our network’s ability to initially confuse the data in two domains.
Specifically, for UDA, inspired by Sun et al. (2016), deep correlation alignment (CORAL) is applied to encoders in source domain: and encoders in target domain: to reduce the domain distribution discrepancy between feature vectors and in source and target domains. We implement this method by appending CORAL loss to original classification loss. CORAL loss measures the distribution discrepancy between source domain and target domain in embedding space. We select a set of feature vectors in source domain from and a set of feature vectors in target domain from .
Specifically, CORAL loss is defined as:
| (3) |
where is the Frobenius norm; is the covariance matrix of and is the covariance matrix of ; and d is the dimension of the feature vectors and . and are calculated by the following equations:
| (4) |
| (5) |
where 1 denotes a column vector whose every element is 1; is number of feature vectors in ; and is the number of feature vectors in .
The combined loss is defined as:
| (6) |
where is the classification loss defined in 2.
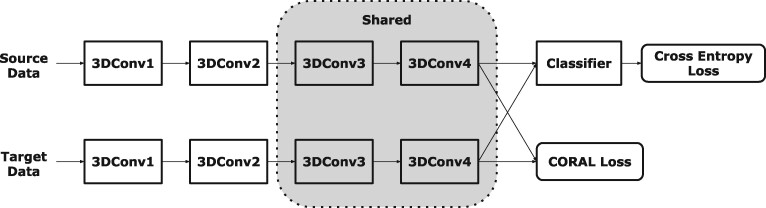
The model architecture of UDA is shown in Figure 2. Generally, and are opposite: trying to diminish must cause category confusion to encoders in source domain: and encoders in target domain: and classifier g and vice versa.
Fig. 2.
Our model architecture of UDA. domain-related layers contain the first and second Convolution Block and domain-independent layers contain the third and last Convolution Block. That is to say, the parameters in the domain-independent layers are shared by data in source domain and target domain
We set α as 500 such that our model can reach a desirable result on target domain.
We simultaneously input data from two domains, and each batch contains data in both target domain and source domain. We acquire and by calculating the batch covariance (Sun et al., 2016) of subtomograms. In other words, denotes the feature vectors in a subtomogram batch from source domain, and denotes the feature vectors in a subtomogram batch from target domain.
Algorithm 2 Unsupervised Domain Adaptation Training
Input:
Subtomograms in source domain.
Subtomograms in target domain.
Output:
Trained encoders and and classifier g.
1: for m epochs do
2: for k steps do
3: Acquire feature vectors batch and from and
4: Calculate the covariance matrix and according to equations 4 and 5.
5: Update the parameters of encoders and and classifier g by minimizing 6.
6: return encoders and and classifier g.
2.2.2. Stage 2.2: update the parameters of discriminator
In this stage, we aim at training a discriminator to differentiate two different domains. To fully utilize the label of target domain, inspired by Motiian et al. (2017), we design the discriminator to identify whether two subtomograms are from the same domain and whether they belong to the same category. We consider the condition that the labeled data in target domain is scarce (for example, not more than 7 samples are labeled in each class). These labeled target samples are utilized in this step. We train a discriminator to distinguish feature vectors and from source domain and target domain with the parameters of encoders in source domain: and encoders in target domain: and classifier g fixed. We combine all of the feature vectors in source domain and labeled feature vectors , and pair feature vectors in . There are four kinds of pair combinations: (i) two paired feature vectors coming from the same domain and category, (ii) from the same domain but different categories, (iii) from different domains but the same category and (iv) from different domains and categories. Therefore, we divide all pairs into four groups: G1, G2, G3 and G4 to correspond four kinds of pair combination above. The discriminator learns to classify each pair into one of the four groups. In each training process, we obtain minibatch by selecting a certain number of feature vector pairs from the 4 groups. The parameters of discriminator are updated by the following equation:
| (7) |
where n denotes the size of minibatch. () represents the ith feature vector pair from minibatch, and . represents the group ID of the ith pair of minibatch. We use the function to denote the discriminator .
The architecture of discriminator is showed in Figure 3. The discriminator contains the 3D discriminator and 1D discriminator corresponding to our partly shared encoder . The output of domain-independent layers (feature vectors ) and output of domain-related layers are both discriminated, because we assume that the input distribution of domain-independent layers has low correlation with domain variation. 3D discriminator distinguishes output domain of domain-related layers. 1D discriminator integrates the output of 3D discriminator and feature vectors then calculates the group ID of each pairs.
Fig. 3.
Our model architecture of SDA (Stages 2.2 and 3)
2.3 Stage 3: fine-tune the encoder
After training the discriminator , we fine-tune the encoders in source domain: and encoders in target domain: and classifier g again with the parameters of discriminator frozen. We need to make discriminator confused between G1 and G2, and also between G3 and G4 by updating the parameters of encoders in source domain: and encoders in target domain: , which is measured by the domain-class discriminator (DCD) loss (Motiian et al., 2017):
| (8) |
where represents the ID of Gi. Therefore, the total loss can be denoted as:
| (9) |
where and are the cross-entropy loss functions to the classification of source domain and target domain.
Algorithm 3 Supervised Domain Adaptation Training
Input:
Cryo-ET data in source domain: .
Labeled cryo-ET data in target domain: .
Output:
Trained encoders in source domain: and encoders in target domain: , classifier g and discriminator .
1: Sample groups G1, G2, G3 and G4
2: for m epochs do
3: Update with encoders in source domain: and encoders in target domain: and classifier g fixed by minimizing 7.
4: for m epochs do
5: Update encoders in source domain: and encoders in target domain: and classifier g with discriminator fixed by minimizing 9.
6: return encoders and , classifier g and discriminator
3 Results
3.1 Datasets
3.1.1. Simulated subtomograms
The simulated subtomograms of 353 voxels are generated similar to the study by Xu et al. (2017). Two simulated subtomogram dataset batches S1, S2 are provided to realize the domain adaptation process. S1 is acquired through 2.2-mm spherical aberration, −10 μm defocus and 300 kV voltage. S2 is acquired through 2-mm spherical aberration, −5 μm defocus and 300 kV voltage. Each dataset batch contains four datasets with different SNR levels (0.03, 0.05, 0.1, 0.5 and 1000). Specifically, there are 43 macromolecular classes in each dataset. All of macromolecular classes are collected from PDB2VOL program (Abola et al., 1984), and each class in each dataset contains 100 subtomograms.
3.1.2. Real subtomogram datasets
We test our model on two real subtomogram datasets S1 and S2. S1 is extracted from rat neuron tomograms (Guo et al., 2018), containing Membrane, Ribosome, TRiC, Single Capped Proteasome, Double Capped Proteasome and NULL class (the subtomogram with no macromolecule). Its SNR is 0.01, and the tilt angle ranges from to .
S 2 is a single particle dataset from EMPIAR (Noble et al., 2018), containing Rabbit Muscle Aldolase, Glutamate Dehydrogenase, DNAB Helicase-helicase, T20S Proteasome, Apoferritin, Hemagglutinin and Insulin-bound Insulin Receptor. Its SNR is 0.5, with tilt angle range to , size 283 voxels, and voxel spacing 0.94 nm.
3.2 Classification results
We conduct experiments, respectively, with fine-tune, FADA and our methods on simulated datasets and real datasets, and compare the results of these methods. Finally, we demonstrate the superiority of our method on the simulated and real datasets.
3.2.1. Results of simulated datasets
In this experiment, As is denoted as source domain and At is denoted as target domain. For facilitating computation, we randomly sample 100 subtomograms from each class. Table 1 presents the prediction accuracy in these methods.
Table 1.
The classification accuracy of the dataset from target domain
| Target domain |
||||||
|---|---|---|---|---|---|---|
| Source domain | SNR | 1000 | 0.5 | 0.1 | 0.05 | 0.03 |
| 1000 | 0.470 | 0.066 | 0.049 | 0.034 | 0.024 | |
| 0.442 | 0.148 | 0.095 | 0.078 | 0.063 | ||
| 0.513 | 0.211 | 0.083 | 0.062 | 0.050 | ||
| 0.664 | 0.404 | 0.185 | 0.161 | 0.146 | ||
| 0.761 | 0.518 | 0.253 | 0.196 | 0.177 | ||
| 0.5 | 0.189 | 0.369 | 0.219 | 0.125 | 0.104 | |
| 0.321 | 0.374 | 0.244 | 0.144 | 0.150 | ||
| 0.387 | 0.416 | 0.204 | 0.137 | 0.111 | ||
| 0.660 | 0.577 | 0.328 | 0.255 | 0.171 | ||
| 0.601 | 0.532 | 0.332 | 0.254 | 0.203 | ||
| 0.1 | 0.107 | 0.24 | 0.237 | 0.188 | 0.166 | |
| 0.125 | 0.250 | 0.230 | 0.166 | 0.143 | ||
| 0.280 | 0.285 | 0.263 | 0.184 | 0.147 | ||
| 0.415 | 0.436 | 0.297 | 0.231 | 0.170 | ||
| 0.513 | 0.456 | 0.332 | 0.257 | 0.218 | ||
| 0.05 | 0.034 | 0.147 | 0.197 | 0.145 | 0.13 | |
| 0.057 | 0.170 | 0.126 | 0.152 | 0.150 | ||
| 0.184 | 0.238 | 0.203 | 0.191 | 0.137 | ||
| 0.280 | 0.292 | 0.231 | 0.205 | 0.176 | ||
| 0.439 | 0.374 | 0.292 | 0.256 | 0.235 | ||
| 0.03 | 0.045 | 0.117 | 0.115 | 0.122 | 0.127 | |
| 0.061 | 0.123 | 0.098 | 0.088 | 0.106 | ||
| 0.089 | 0.190 | 0.166 | 0.166 | 0.148 | ||
| 0.276 | 0.229 | 0.202 | 0.194 | 0.177 | ||
| 0.218 | 0.243 | 0.211 | 0.200 | 0.200 | ||
Note: The result in each cell represents the accuracy of CORAL (Sun and Saenko, 2016), Sliced Wasserstein Distance (Gabourie et al., 2020), fine-tune, FADA and our method from top to bottom. The highest accuracy in each cell is highlighted. It shows that the prediction accuracy of our method surpasses the baseline methods in most of the cases.
3.2.2. Results of cross-domain prediction of real subtomograms
The real datasets are acquired in the very complicated environment, causing the heterogeneity of subtomograms and very low SNR comparing to simulated dataset. This characteristic of experimantal datasets poses a challenge to the macromolecule classification.
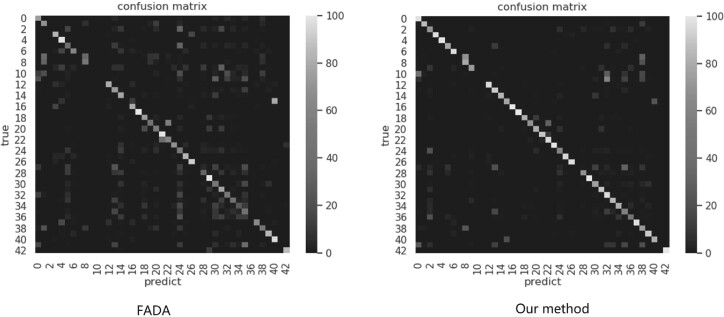
Five simulated datasets in As and At with different SNRs (1000, 0.5, 0.1, 0.05 and 0.03) are utilized. Each of the simulated dataset acts as source domain, and their classes are the same as target domain.A two real subtomogram datasets acted as the target domain. Table 2 shows the classification results on all of the methods. The result in each cell represents the prediction accuracy in real dataset, and the confusion matrices have been showed in (Fig. 4). Additionally, 3 and 7 labeled samples are selected in target domain for supervised training in FADA and our method.
Table 2.
The classification accuracy on the real dataset
| Target domain |
|||||||
|---|---|---|---|---|---|---|---|
| 1000 | 0.5 | 0.1 | 0.05 | 0.03 | |||
| Source domain | Three shot | S 1 | 0.801 | 0.626 | 0.453 | 0.535 | 0.538 |
| 0.732 | 0.720 | 0.608 | 0.606 | 0.586 | |||
| S 2 | 0.705 | 0.731 | 0.793 | 0.748 | 0.655 | ||
| 0.788 | 0.733 | 0.891 | 0.849 | 0.774 | |||
| Seven shot | S 1 | 0.842 | 0.664 | 0.760 | 0.679 | 0.690 | |
| 0.774 | 0.805 | 0.791 | 0.719 | 0.701 | |||
| S 2 | 0.959 | 0.952 | 0.947 | 0.953 | 0.796 | ||
| 0.833 | 0.969 | 0.971 | 0.954 | 0.958 | |||
Notes: The result in each cell represents the accuracy of CORAL (Sun and Saenko, 2016), Sliced Wasserstein Distance (Gabourie et al., 2020), fine-tune, FADA and our method from top to bottom. The highest accuracy in each cell is highlighted. It shows that the prediction accuracy of our method surpasses the baseline methods in most of the cases. The highest accuracy in each cell is highlighted.
Fig. 4.
The confusion matrix in our method and baseline method. In view that FADA is far more better than other baselines, we compare the confusion matrix in our method to those in FADA. The left is the confusion matrix of FADA, the right is the confusion matrix of our method
4 Conclusion
Recently, cryo-ET emerges as a powerful tool for systematic in situ visualization of the structural and spatial information of macromolecules in single cells. However, due to high structural complexity and the imaging limits, the classification of subtomograms is very difficult. Supervised deep learning has become the most powerful method for large-scale subtomogram classification. However, the construction of high-quality training data is laborious. In such case, it is beneficial to utilize another already annotated dataset to train neural network model. However, there often exists a systematic image intensity distribution difference between the annotated dataset and target dataset. In such case, the model trained on another annotated dataset may have a poor performance in target domain. In this article, we propose a Few-shot Domain Adaptation method to for cross-domain subtomogram classification. Our method combines UDA and SDA: we first train a discriminator to identify the domain of each subtomogram, and we utilize the discriminator to assist us the process of SDA. To the best of our knowledge, this is the first work to apply semisupervised Domain Adaptation on subtomogram classification. We conduct experiments on simulated dataset and real dataset, and the prediction accuracy of our methods surpasses the baseline methods. Therefore, our method can be effectively applied to the subtomogram classification from a new domain with only a few labeled samples supplied. Our work represents an important step toward fully utilizing deep learning for subtomogram classification, which is critical for the large-scale and systematic in situ recognition and recovery of macromolecular structures in single cells captured by cryo-ET.
Funding
This work was supported in part by U.S. National Institutes of Health (NIH) grant [P41GM103712 and R01GM134020], U.S. National Science Foundation (NSF) grant [DBI-1949629 and IIS-2007595] and Mark Foundation for Cancer Research grant [19-044-ASP]. X.Z. was supported by a fellowship from Carnegie Mellon University’s Center for Machine Learning and Health.
Conflict of Interest: none declared.
Supplementary Material
References
- Abola E.E. et al. (1984) The protein data bank. In: Neutrons in Biology. Springer, Switzerland, pp. 441–441. [Google Scholar]
- Alam M.J. et al. (2018) Speaker verification in mismatched conditions with frustratingly easy domain adaptation. In Odyssey, Les Sables d’Olonne, France, pp. 176–180.
- Bartesaghi A. et al. (2008) Classification and 3D averaging with missing wedge correction in biological electron tomography. J. Struct. Biol., 162, 436–450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blitzer J. et al. (2006) Domain adaptation with structural correspondence learning. In Proceedings of the 2006 conference on empirical methods in natural language processing. Association for Computational Linguistics, Sydney, Australia, pp. 120–128.
- Briggs J.A. (2013) Structural biology in situ-the potential of subtomogram averaging. Curr. Opin. Struct. Biol., 23, 261–267. [DOI] [PubMed] [Google Scholar]
- Che C. et al. (2018) Improved deep learning-based macromolecules structure classification from electron cryo-tomograms. Mach. Vis. Appl., 29, 1227–1236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gabourie A.J. et al. (2020) System and method for unsupervised domain adaptation via sliced-wasserstein distance. US Patent App. 16/719,668.
- Garcia-Romero D. et al. (2014) Supervised domain adaptation for i-vector based speaker recognition. In: 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), IEEE, Piscataway, NJ, pp. 4047–4051.
- Guo Q. et al. (2018) In situ structure of neuronal C9orf72 poly-GA aggregates reveals proteasome recruitment. Cell, 172, 696–705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irobalieva R.N. et al. (2016) Cellular structural biology as revealed by cryo-electron tomography. J. Cell. Sci., 129, 469–476. [DOI] [PubMed] [Google Scholar]
- Long M. et al. (2016) Unsupervised domain adaptation with residual transfer networks. In: Advances in Neural Information Processing Systems, pp. 136–144.
- Motiian S. et al. (2017) Few-shot adversarial domain adaptation. In: Advances in Neural Information Processing Systems, NIPS, San Diego, CA, USA, pp. 6670–6680.
- Noble A.J. et al. (2018) Reducing effects of particle adsorption to the air–water interface in cryo-em. Nat. Methods, 15, 793–795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quionero-Candela J. et al. (2009) Dataset Shift in Machine Learning. The MIT Press, Cambridge, MA. [Google Scholar]
- Sun B. et al. (2016) Deep coral: correlation alignment for deep domain adaptation. In: European Conference on Computer Vision, Springer, Switzerland, pp. 443–450. [Google Scholar]
- Xu M. et al. (2017) Deep learning-based subdivision approach for large scale macromolecules structure recovery from electron cryo tomograms. Bioinformatics, 33, i13–i22. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.