Abstract
Primary care plays a vital role for individuals and families in accessing care, keeping well, and improving quality of life. However, the complexities and uncertainties in the primary care delivery system (e.g., patient no-shows/walk-ins, staffing shortage, COVID-19 pandemic) have brought significant challenges in its operations management, which can potentially lead to poor patient outcomes and negative primary care operations (e.g., loss of productivity, inefficiency). This paper presents a decision analytics approach developed based on predictive analytics and hybrid simulation to better facilitate management of the underlying complexities and uncertainties in primary care operations. A case study was conducted in a local family medicine clinic to demonstrate the use of this approach for patient no-show management. In this case study, a patient no-show prediction model was used in conjunction with an integrated agent-based and discrete-event simulation model to design and evaluate double-booking strategies. Using the predicted patient no-show information, a prediction-based double-booking strategy was created and compared against two other strategies, namely random and designated time. Scenario-based experiments were then conducted to examine the impacts of different double-booking strategies on clinic’s operational outcomes, focusing on the trade-offs between the clinic productivity (measured by daily patient throughput) and efficiency (measured by visit cycle and patient wait time for doctor). The results showed that the best productivity-efficiency balance was derived under the prediction-based double-booking strategy. The proposed hybrid decision analytics approach has the potential to better support decision-making in primary care operations management and improve the system’s performance. Further, it can be generalized in the context of various healthcare settings for broader applications.
Keywords: primary care, decision-making, prediction, simulation, patient no-show, double-booking
1. Introduction
Primary care serves as the cornerstone of the U.S. healthcare system. Starfield [1] conceptualized the vital role and value of primary care by 4 C’s: first contact (access and use of health services whenever necessary), continuity (establishment of long-term care), comprehensive (promotion, prevention, treatment and rehabilitation appropriate to the primary care context), and coordination (the integration of all the care the user receives and needs with the other health services) [2]. Empirical evidence has shown that greater utilization of primary care is associated with better health outcomes (e.g., lower mortality rate, lower premature death rate, higher life expectancy, and higher satisfaction with the healthcare system), better healthcare operations outcomes (e.g., less unnecessary use of more expensive healthcare services, such as hospitalizations and emergency department or ED visits), and lower healthcare costs [3]-[6]. However, the complexities and uncertainties in the primary care delivery system have brought significant challenges into its operations management, which can potentially lead to poor outcomes of patient health and satisfaction, as well as primary care operations (e.g., accessibility, productivity, efficiency). These challenges include, but are not limited to, managing increased demand of primary care with limited supply of healthcare workforce (e.g., doctors, nurses), handling uncertainties (e.g., patient no-shows, late cancellations, late arrivals, walk-ins, etc.) and disruptions (e.g., shut down of services due to extreme events such as pandemics), and incorporating new technologies and tools (e.g., tele-medicine) into current operations.
Significant research efforts have been made to address these challenges. For example, Shi, et al. (2014) [7] conducted a simulation analysis to examine and improve the patient visit efficiency at a VA primary care clinic. Faridimehr, et al. (2019) [8] developed a stochastic optimization model to identify effective appointment scheduling templates in primary care clinics. Chand, et al. (2009) [9] used a structured process analysis to improve the patient flow at an outpatient clinic by identifying and addressing the sources of variability and improvement factors. Focusing on outpatient delivery systems, Huang (2016) [10] proposed and implemented an idea of redesigning patient scheduling groups (e.g., urgent care, follow-up, new patient, office visit, physician exam, and well care) for improving the effectiveness of appointment system using a simulation-optimization technique. In these studies, various analytical approaches were employed to provide valuable information for supporting decision-making in primary care operations. Some well-established analytical approaches that have been commonly used in prior literature include, but not limited to, mathematical optimization, computer simulation, and process improvement. In the past decades, machine learning and data analytics research have grown exponentially due to the availability of tremendous health data, with their applications in healthcare showing great promise. Based on a literature review, Kang et al. (2020) [11] discussed the possible uses of machine learning in primary care to reduce the burden of missed diagnostic opportunities and maximize the quality of care provided <cite>. Yang et al. (2022) [12] identified the key domains for machine learning integration in primary care to support care delivery transformation <cite>.
While these analytical approaches can provide great supports in healthcare decision-making, some limitations of the existing approaches and potential areas for further improving the decision analytics capability are realized. First, the majority of current models developed based on simulation or optimization methods are at the macroscopic (or aggregated) level. Hence, the microscopic (or individual) level behavior of the system (e.g., the heterogeneous behaviors of patients and providers) cannot be well represented, which may consequently affect the quality of decisions derived from these approaches. Second, although there is extensive machine learning literature in healthcare, a large portion of them focuses on predictions of patients’ clinical outcomes (e.g., disease risks and diagnosis). Studies on predicting operation related variables of the primary care system (e.g., patient no-show behavior, visit cycle time) are still lacking. Third, while machine learning models help identify the predictors to specific outcomes, they cannot be used directly for evaluating or optimizing decisions. Leveraging predictive analytics in decision modeling (e.g., simulation or optimization models) has a great potential to incorporate information on uncertainties and thus better support decision-making and improve primary care operations’ performance.
The major contribution of this study is the development of a predictive decision analytics approach to improve the areas mentioned above. This approach consists of three major modules, predictive analytics, simulation modeling, and decision evaluation. Here, the simulation modeling module integrates two simulation methods, i.e., agent-based simulation (ABS) and discrete-event simulation (DES). These three modules are interconnected. By conducting predictive analytics, more accurate information about the primary care operations can be generated and used as input data to inform the hybrid ABS-DES model such that the primary care system can be more realistically represented. Based on this hybrid simulation model, the system behavior can be better understood at both aggregated and individual levels and various decisions (“what-if” scenarios) can be more rigorously tested and evaluated. Via the connections between these modules, this approach holds a great promise to further advance the decision-making capacity and enable more cost-effective solutions in healthcare operations. A conceptual framework that generalizes the high-level designs of these modules was devised, which could be applied for operational decision support in various healthcare settings. Further, we conducted a case study in a large non-profit family medicine clinic to demonstrate how this framework was applied to help make double-booking decisions in reducing the impacts of patient no-shows. Patient no-shows present a major and persistent concern in primary care. A study [13] that analyzed the patient no-show data over a 12-year period in 10 different types of clinics (including primary care and specialty care such as cardiology, dermatology, mental health, etc.) found that primary care had the highest total number of no-shows (an average of 33,098 no-shows among 185, 945 visits per year, or 17.8% no-show rate). The two main objectives of the case study included: (1) to predict patient no-shows and develop a double-booking strategy based on the predicted information, i.e., prediction-based double-booking strategy, (2) to evaluate the performance of this double-booking strategy based on simulated primary care operations.
The remaining article is organized as follows. Section 2 provides a brief literature review on the applications of existing methods used in healthcare operations management. Then, a conceptual framework of the proposed hybrid decision analytics approach is presented in Section 3, followed by a case study in Section 4. Finally, Section 5 concludes the study.
2. Literature Review
In this section, we first present a brief literature review on the analytical approaches used for decision support in a broad context of healthcare settings, and then summarize their applications in primary care for appointment overbooking.
2.1. Analytical Approaches
Quantitative research plays an important role in assessing and improving the performance of healthcare system and quality of care. In this type of research, analytical approaches are often adopted to model the system’s behavior and solve decision-making problems. The commonly used approaches in existing literature include simulation modeling, mathematical optimization, process analysis, machine learning, and hybrid approaches (e.g., simulation-based optimization). Of particular interest, the discussion below focuses on the applications of machine learning and simulation modeling approaches.
In the context of predicting healthcare operation related variables, there are various machine learning techniques that have been used (e.g., regression, decision tree, random forest, support vector machine, and ensemble methods). For instance, regression models were used for early detection of no-shows of primary care patients [14–15], emergency department (ED) patients with prolonged length of stay [16] and hospital patients with early readmissions [17]. Decision trees for classification problems were used to predict hospital no-show appointments [18] and 30-day hospital readmission rates [19]. Random forests were used to predict patient length of stay in a hospital setting [20], discharge destination from inpatients for hip-fracture patients [21], and healthcare expenditure using neighborhood variables [22]. A mixed-ensemble method that involved logistic regression, support vector machine, decision tree, etc. was used to predict hospital readmission [23]. Focusing on patient no-show prediction, a systematic review found that logistic regression was the most used technique [24]. The same review also revealed that only a single study among the 50 selected articles attained an area under the curve greater than 0.9. While the large size of healthcare data (e.g., electronic health records or EHRs) offers great potentials for making the predictions, further research is needed to improve the model accuracy.
Simulation modeling has been used to model healthcare systems for more than 40 years [25]. System dynamics (SD), discrete-event simulation (DES), and agent-based simulation (ABS) are the three common simulation approaches. SD provides a holistic view of the system by modeling the behavior of systems over time at an aggregated level [26–27]. It has been used to evaluate healthcare policies by examining their impacts on both tangible elements (e.g., waiting time and costs) and intangible elements (e.g., work pressure, patient anxiety) [26]. Some additional SD applications include public health policy evaluation [28], epidemic prevention/suppression strategies [29], healthcare infrastructure modeling [30], and health economic models [31]. DES is a process-oriented simulation approach which has been widely used to model the queueing systems. Many studies used DES to evaluate the impacts of staffing, appointment scheduling, bed capacity planning, and use of technology on process-related performance measures (e.g., patient wait times and staff utilization) toward improving the healthcare delivery processes [32–40]. Different from the two top-down approaches (i.e., SD and DES), ABS is a bottom-up approach in which the aggregated-level system dynamics is completely driven by the behavior of agents and their interactions at the individual level. The agents are goal-oriented computer entities and can make decisions autonomously [41]. ABS is particularly suited to model complex systems that involve many non-linear interactions. Taboada et al. (2013) [42] used ABS to predict the effects of patient deviation policies in emergency departments (EDs). Wang (2009) [43] and Laskowski & Mukhi (2008) [44] used ABS to model ED workflow, staffing, and patient admission scheduling. Kaushal et al. (2015) [45] used ABS to evaluate ED fast track strategies to reduce patient wait times. Furthermore, hybrid simulation is a modeling approach that has received growing attentions in recent years. It provides modelers with the flexibility of combining two or three simulation approaches mentioned above and thus offers more advanced capabilities in modeling complex systems. Hybrid simulation can be used to model different aspects of the same complex system which cannot be captured by a single simulation approach [46]. The application of DES-SD hybrid simulation was seen in Viana et al. (2014) [47], where DES captured the operation of a hospital outpatient clinic and SD modeled the infection process in the community. Tejada et al. (2014) [48] used SD to model the overall structure and operation to detect breast cancer in the U.S., while DES was used to simulate the screening policies and treatment procedures. Anagnostou et al. (2013) [49] used the DES-ABS hybrid approach within the context of emergency medical services, where ABM modeled the behavior of ambulance services and DES represented the process flow of emergency department operations.
2.2. Overbooking Strategies
Overbooking is one of the appointment scheduling practices that has been adopted widely in healthcare settings to alleviate the negative impacts of patient no-shows and late cancellations [50–52]. To generate more effective appointment schedules and overbooking strategies, a great deal of research has been conducted in various healthcare settings. Xie et al. (2022) [53] introduced a queueing model to investigate the backlog dynamics of appointments in outpatient clinics where the patient no-show behavior and different overbooking strategies were taken into consideration and examined to reduce the backlogs. Zeng et al. (2010) [54] formulated and solved the clinical scheduling with overbooking as an optimization problem and identified properties of an optimal schedule with heterogeneous patients having different no-show probabilities. The optimization problem of appointment scheduling and overbooking was also studied in a medical imaging facility setting. Chen et al. (2018) [55] proposed a two-stage deterministic equivalent of the stochastic optimization problem to simultaneously optimize overbooking and scheduling decisions and Kuo et al. (2020) [56] utilizes a stochastic mixed-integer linear program to generate optimal schedules with overbooking that could help balance the tradeoffs between schedule efficiency and accessibility to service.
This literature review shows a lack of approaches to support predictive decision-making in the context of healthcare operations. Although such predictive approaches have been developed for decades in disease screening, diagnosis, and treatment, it is still in their infant stage for operations management of healthcare delivery systems. Further, there is little attention paid to predict variables pertinent to healthcare operations and further design and evaluate decisions using the prediction results. This study is motivated to alleviate this gap by linking predictions to decision-making towards better primary care operations.
3. Materials and Methods
This study proposes a hybrid decision analytics approach to facilitate predicted decision-making in primary care operations. Distinguished from the existing approaches, the proposed approach employs predictive analytics in conjunction with simulation modeling to design and evaluate operational decisions, where the predicted information is generated and used to derive possible interventions that tend to be more targeted, and potentially more precise, toward improving the performance of the underlying operations. Figure 1 presents a conceptual framework of the approach which consists of three major modules: predictive analytics, simulation modeling, and decision analytics. Although it is devised in the primary care context, this approach can be applied to support operational decision-making in a broader healthcare context (e.g., acute care, home care).
Figure 1.

A conceptual framework of the hybrid decision analytics approach
3.1. Predictive Analytics
The predictive analytics module initializes the decision-making process by making predictions on variables (i.e., outcome variable) that are pertinent to primary care operations, such as patient no-shows, late arrivals, visit time, etc. As these outcome variables are often already labelled, supervised learning techniques (e.g., linear and logistic regression, random forests, decision trees, and support vector machines) often employed to make the predictions. Supervised learning problems can be further divided into regression and classification problems. A regression problem is when the outcome variable is a real or continuous value, whereas a classification problem is when the output variable is a category. The predicted information has two major uses in the approach. First, it can be used to assign values of the corresponding simulation input parameters (non-decision-variables) at an individual level, which could be more accurate than those derived at an aggregated level from the traditional input data analysis (e.g., data fitting techniques). Second, it can be used to generate targeted and more precise decisions (decision variables) at the group or individual level. For instance, the patient no-show prediction can help design double-booking strategies by identifying specific patient appointments that should be double booked (i.e., appointments for patients with a high risk of no-show) such that the undesirable impacts due to inappropriate double-booking schedules can be reduced (e.g., increased patient wait time if the patients for both originally scheduled and double-booked appointments show up).
Because of the availability of tremendous healthcare data, there are many predictor candidates for the predictive analytics. One of the most widely used data sources is the EHR systems, which contain a great deal of patient medical information in various formats, structured (e.g., numeric, categorical) and unstructured (e.g., text). Some examples are patient demographics (e.g., age, gender, race), social determinants (e.g., insurance payor, if the patient has a primary care physician or not), clinical data (e.g., diagnosis, medication, visit history, problem list, vital signs, lab results), appointment schedule data (e.g., reason for visit, appointment type, scheduled time), and encounter data (e.g., patient arrival/check-in time, appointment status, modality). Here, it is also worthwhile mentioning some common issues in predictive analytics which could significantly affect the quality of prediction models, such as missing data, collinearity between predictors, imbalanced classes of outcome variables, overfitting/underfitting, etc. It is very important to apply appropriate methods to handle these issues carefully.
3.2. Simulation Modeling
The simulation modeling module consists of a computer simulation model, which is used to provide an explicit representation of the primary care operation. This model integrates the discrete-event simulation (DES) and agent-based simulation (ABS) approaches, where the DES model is developed to represent the patient flow at the primary care settings and the ABS model is developed to govern the micro-level behaviors of patients, doctors, and staff (including their interactions). Figure 2 shows a high-level design of this DES-ABS model.
Figure 2.
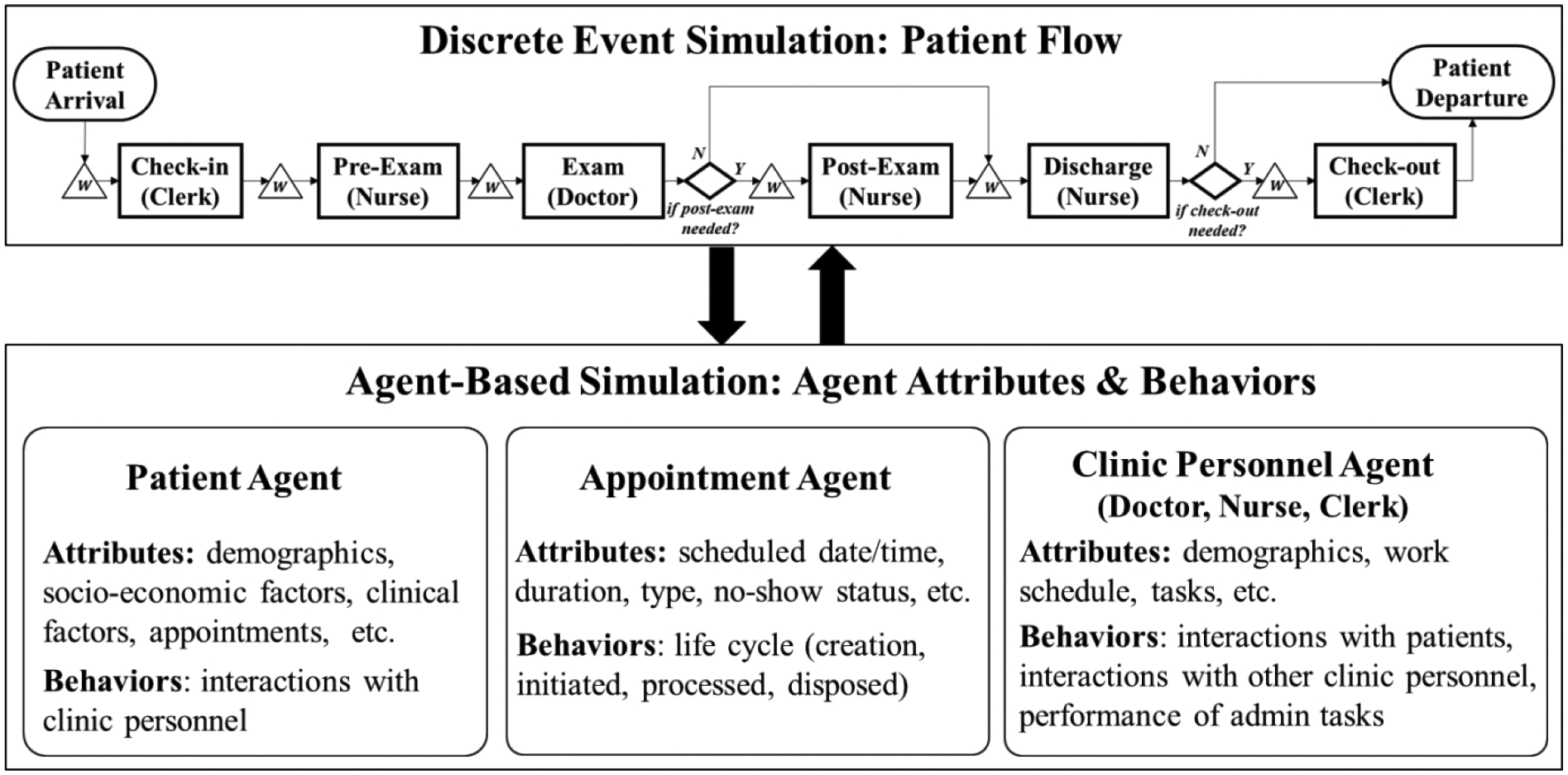
A high-level DES-ABS simulation design
3.2.1. Discrete-Event Simulation (DES)
The core of this DES model is the patient flow – a key process in the primary care operations. Figure 1 shows a generic primary care patient flow for in-person visits. Entities, resources, and activities involved in the patient flow are the key modeling elements. The patient appointments are identified as the model entities which flow through the system. The primary resources include clinical personnel (e.g., doctors, nurses, and clerks), exam rooms, and medical equipment. The major patient-flow activities include check-in, pre-exam, exam, post-exam (upon doctor’s request), discharge, and check-out (may be combined with “discharge”). Although this design focuses on the patient flow of in-person visits, the DES model can be used to capture the patient flow of tele-health visits as well as other processes in the primary care operations. It is worthwhile mentioning that, although the ABS model has the capability to model any process, the use of the DES model can offer several unique benefits. First, it provides a natural view of (linear) processes. The DES model visualization (animation) can help identify the bottlenecks in the process. Second, it generates process related statistics (e.g., entities’ average wait time for specific activities and total time in system, length of queues) easily as many DES packages provide the reporting functions. Third, it generally requires less time in model design and implementation (i.e., more efficient) compared to ABS for modeling the same process.
3.2.2. Agent-Based Simulation (ABS)
The core of this ABS model are the agents involved in the primary care settings, including patients, clinic personnel (e.g., doctors, nurses, clerks), patient appointments, exam rooms, orders, etc. The attributes and behaviors of agents are key modeling elements. Some examples of agents’ attributes and behaviors associated with patients, clinic personnel, and appointments are presented in Figure 1. In general, the ABS model design involves three major tasks: (1) design agents (by types or classes), agents’ attributes and behavior rules, (2) design interactions between agents, and (3) design the environment (e.g., a spatial context) and interactions between agents and the environment. The primary use of the ABS model is to capture the micro-level behaviors of agents as well as their (non-linear) interactions in primary care operations. Figure 3 depicts a generic flow chart that dictates the logic of clinic personnel’s working behavior.
Figure 3.

A general flow chart of clinic personnel working behavior logic
The interactions between clinical personnel (e.g., doctor-doctor, nurse-nurse, doctor-nurse) can be governed by agents’ communications within ABS, whereas the interactions between patients and clinic personnel are governed by the patient flow in DES, therefore an integration between DES and ABS is developed to model patient-clinic personnel interactions. The dynamics of entities’ queues in DES (i.e., queues waiting for resources) is triggered by the status of resource agents in ABS (“busy” or “idle”) and vice versa. Note that both entities and resources in DES are represented as agents in ABS. For example, when a doctor agent finishes the current “EHR documentation” activity in ABS, it becomes available to handle the first patient appointment waiting in the queue for the “Exam” activity in DES. Then, after this activity is finished, the doctor agent would proceed to the next activity in ABS (e.g., go to handle the next patient appointment in the queue or other activity if no appointment is currently in the queue).
3.3. Decision Evaluation
In this study, “decisions” refer to any policies, interventions, strategies, and tactics involved in primary care operations. Based on simulation modeling, there are two types of decision analytics: (simulation-based) optimization and evaluation. While the prior one seeks the optimal decision over the solution space globally or locally, the latter one seeks the best decision over a relatively small solution space which is not necessarily the optimal solution. Both types of decision analytics involve an implementation of a set of hypothesized scenarios (computer experiments) in the simulation model and an evaluation of these scenarios based on the pre-established outcome measure(s). Design of experiments methods, such as full/partial factorial design and response surface methodology, provide a scientific way to generate scenarios such that valid statistical inferences can be drawn on the initial and long-term average behavior of the system. A set of experimental factors (or decision variables) are needed to design the experiments, where each factor may have multiple levels (one factor level can denote a certain value of the experimental factor within its possible range). In prior research, a number of outcome measures have been established for evaluating the performance of healthcare operations, including but not limited to, process efficiency measures (e.g., patient wait time), clinic productivity measures (e.g., clinic throughput), and resource utilization measures (e.g., utilization of doctors and nurses). The evaluation of these outcome measures requires an output analysis, which is the analysis of data generated by simulation runs – multiple runs are always necessary in stochastic simulations – to assess/predict system performance or compare performance of two or more decisions.
4. Case Study
A case study was conducted in a local family medicine clinic to demonstrate the use of the proposed approach in design and evaluation of double-booking strategies for patient no-show management. In the study clinic, the situation of patient no-shows was a major concern: among an average of 28,000 clinic visits per year before the COVID-19 pandemic, approximately 6,000 original patient appointments were missed due to patient no-shows (i.e., 21.4% no-show rate). These no-show cases have resulted in negative impacts on both the clinic’s operations (e.g., decreased productivity, financial loss) and the patients (e.g., missed care, reduced access to care). Double-booking has been used in many clinics as one of the common practices to alleviate the impacts of patient no-shows. While it offers an opportunity for other patients to access the care, it also helps the clinics to maintain an expected level of operations. However, without appropriate strategies, double-booking could also result in undesirable consequences, including longer patient wait time as well as doctor/staff overtime. In this case study, we first conducted predictive analytics for patient no-shows and used the prediction results to design the double-booking strategies (i.e., prediction-based double-booking strategies). Then, we created an integrated DES-ABS model for representing the clinic’s operations and used it to evaluate the impacts of the prediction-based double-booking strategies against two other strategies (i.e., random and designated time). This study was approved by the Institutional Review Board of The University of Texas at Arlington.
4.1. Predictive Analytics for Patient No-Shows
A data set of 3-month (October to December 2019, Pre-COVID) patient encounter records was used for the prediction of patient no-shows. This data set was extracted from the clinic’s EHR system, and all the identifiable information of patients and clinic personnel was encrypted by the clinic’s data analyst. The data set contained 9,822 patient encounter records, which was split by 70% and 30% for training and testing, respectively. The single response variable was the appointment status, coded by a dichotomous variable (1 = no-show and 0 = completed). The predictor variables included patient demographics (age group, gender, race, ethnicity, primary language, payor type) and appointment schedule information (type, date & time, duration). Two commonly used prediction models, logistic regression [57] and random forest [58], were applied in this prediction for the demonstration purpose of the proposed approach. Table 1 compares the prediction performances of these two models. The no-show prediction results derived from the random forest model were used for designing the prediction-based double-booking strategies, although the overall performance of the logistic regression appeared to be better. This was mainly because of the higher sensitivity (or hit rate) of the random forest model compared to the logistic regression model (0.28 vs. 0.16), which allowed relatively better detection of the no-show cases when they actually presented.
Table 1.
Comparison of prediction model performances
| Logistic Regression | Random Forest | |
|---|---|---|
| Accuracy | 0.75 | 0.72 |
| Sensitivity | 0.16 | 0.28 |
| Specificity | 0.96 | 0.88 |
| AUC* | 0.67 | 0.63 |
Area Under the receiver operating characteristic Curve
4.2. Simulation Modeling for Clinic Operations
The input data for simulation modeling, including patient encounter records and the clinic’s operational data, were collected via mixed methods. Table 2 provides a list of the specific simulation inputs and the corresponding data collection methods.
Table 2.
Simulation input data
| Data Category | Data Item | Data Collection Method |
|---|---|---|
| Patient encounter records | Patient data: id (de-identified), age group, gender, race/ethnicity, language, payor type | Data extraction from the EHR system |
| Appointment data: scheduled time/duration, check-in/out time, primary care provider (de-identified), appointment type*, modality**, status*** | ||
| Clinic’s operational data | Patient flow data: tasks/activities of doctors, nurses, and clerks, task/activity sequences | Focus groups |
| Patient flow data (with timestamp): duration of tasks/activities (e.g., check-in duration, exam duration, etc.) | Direct observations | |
| Staff schedule: daily capacity of nurses and clerks at an aggregated level | Other methods (e.g., consultation with the clinic staff) | |
| Doctor schedule: daily schedule of doctors at an individual level |
Appointment type includes new patient, follow-up, well child, preventive care visits, etc.
Appointment modality includes in-person, tele-health, and phone.
Appointment status includes complete, no-show, cancelled, and left without being seen.
The simulation model was implemented in AnyLogic ® (University Edition 8.7.9), a Java-based multi-method simulation toolkit. The model resembled one-week pre-COVID operation of the clinic, where both double-booked and no-show appointments were presented. During the study week, there was a total of 1,074 appointments, among which 32 were double booked. The average no-show rate was 23.2%. Table 3 shows the initial values of the input parameters. The model was executed for 10 replications. The execution time was approximately 2 hours.
Table 3.
Initial values of simulation input parameters
| Input Parameter | Data Level | Value |
|---|---|---|
| Patient arrival | Individual | The check-in time of each appointment in the original patient encounter data |
| Check-in duration | Individual |
N (15, 5, 10, 20) for new patients* N (3, 1, 2, 5) for established patients |
| Pre-exam duration | Individual | N (9, 4, 2, 24) |
| Exam duration | Individual |
N (44, 16, 8, 79) for new patients N (24, 16, 5, 42) for established patients |
| Post-exam duration and probability | Individual | N (24, 10, 15, 45); 0.1 |
| Discharge duration | Individual | N (8, 2, 5, 20) |
| Number of CMAs ** | Aggregated | {10, 10, 11, 10, 9} |
| Number of LVNs | Aggregated | {8, 7, 8, 8, 7} |
| Number of clerks | Aggregated | {5, 5, 5, 5, 5} |
All the activity durations were generated for new and established patients, respectively. Truncatednormal distributions were used to represent activity durations, expressed by N(μ, σ, min, max).
The numbers of clinic staff from Monday to Friday during the study week.
Model verification was conducted by testing the statistical significance of the differences between the simulation outputs and the observed data. Two variables were used in the hypothesis testing: visit cycle time (i.e., time elapsed from patient arrival to departure) and patient wait time for doctor (i.e., time elapsed from the time when the CMA finishes pre-exam to the time when the doctor first enters the room). The t-test results showed that there were no significant differences between the simulated and observed patient cycle time (p-value = 0.65) as well as patient wait time for doctor (p-value = 0.96).
4.3. Experimentation
Simulation experiments were conducted to examine the impacts of different double-booking strategies on clinic’s efficiency and productivity. In this study, the efficiency was measured by the patient cycle time and wait time for doctor, and the productivity was measured by the daily clinic throughput (i.e., number of visits or patient volume).
Baseline Scenario:
A hypothetical scenario was generated as the baseline to represent the “expected” operation of the clinic. In this scenario, all the patients were assumed to show up for their scheduled appointments, and thus double-booking was not used (i.e., no intervention). To create the baseline scenario, the following rule was used: when a doctor’s time slot was filled by more than one appointment in the original one-week patient encounter data, only one appointment was kept. All other appointments scheduled for the same time slot were then removed. The simulated operational outcomes derived from this baseline scenario were used as the benchmark values to evaluate the impacts of various double-booking strategies.
Double-Booking Strategies and Experimental Scenarios:
This study evaluated three double-booking (DB) strategies: (1) prediction-based, (2) random, and (3) designated time. A general description of each strategy was provided below, which included the strategy-specific experimental factor(s) used for generating possible DB scenarios.
Predication-Based DB Strategy. This strategy determines the specific patient appointments (doctor’s time slots) for double-booking based on the prediction results of patient no-shows. The intention is to double book the time slots scheduled for those patients who are most likely to not show up for their appointments. This strategy has a single experimental factor, which is the cut-off value (i.e., a probability) used for identifying the no-show cases, denoted by pPred.
Random DB Strategy. This strategy randomizes the selection of doctors as well as their scheduled appointments for double-booking. The random selection procedure can be described as follows. For a particular day j, a certain number of doctors are first chosen randomly from a list of doctors who were working on that day, denoted by . Then, for the doctor i selected on day j, a certain number of appointments that have already been scheduled for this doctor will be selected for double-booking, denoted by . There are two experimental factors associated with this strategy, i.e., and .
Designated Time DB Strategy. In this strategy, only those time slots within certain specified time period(s) of the day are possible for double-booking. This study specified two time periods separately: early morning (before 9AM) and early afternoon (between 12PM-2PM). The experimental factors of this strategy are the number of double-booked time slots in the early morning and early afternoon on a particular day j, denoted by and , respectively.
Table 4 lists all the double-booking scenarios evaluated in this study. To simulate the appointments added for double-booking, hypothetical patient encounter records were generated by replicating the original records, except for the no-show status. The no-show statuses of all the hypothetical appointments were assigned randomly based on the average no-show rate of the study week (i.e., 23.2%).
Table 4.
Experimental scenarios under the three double-booking strategies
| DB Strategy | Experimental Factors | Values |
|---|---|---|
| Prediction-Based | pPred: Probability used to identify no-shows | 0.7, 0.6, 0.5, 0.4, 0.3 |
| Random | : Number of doctors selected for double-booking on day j | 10, 16, 11, 15, 12* |
| : Number of scheduled appointments with doctor i selected for double-booking on day j | 10%, 20%, 30%, 40%, 50%** | |
| Designated Time | : Percentage (%) of the total available time slots in early AM | 10%, 30%, 50%, 70%, 90%, 100% |
| : Percentage (%) of the total available time slots in early PM | 10%, 30%, 50%, 70%, 90%, 100% |
Number of doctors selected on Monday through Friday during the study week, respectively.
= total number of scheduled appointments with doctor i on day j × a percentage. This percentage was used as a substitute for the experimental factor . Once the factor level was set (e.g., 10%), it was applied to all the selected doctors from Monday to Friday of the study week.
4.4. Results and Findings
Table 5 summarizes the experimental results of the two efficiency metrics, i.e., visit cycle time (VCT) and patient wait time for doctor (PWTD). In the baseline scenario (no DB), these two metrics were found to be 71.1 and 14.4 minutes, respectively. When a DB strategy was used, the clinic efficiency decreased along with the increased number of double-booked appointments, as expected. Among all the scenarios, the shortest VCT (71.6 minutes; 0.7% increase from the baseline) and PWTD (14.8 minutes; 2.8% increase from the baseline) were found under the designated early PM strategy (10%), which only had 12 DB appointments during the entire study week (an average of 2.4 per day or 1.3% of the total daily appointments). On the other hand, the longest VCT (96.4 minutes; 26.6% increase from the baseline) and PWTD (34.5 minutes; 136.3% increase from the baseline) were observed when the designated early AM strategy (100%) was used, which had a total of 187 double-booked appointments during the study week (an average of 37.4 per day or 19.5% of the total daily appointments). Further, it was noted that PWTD contributed a significant portion of VCT, ranging from 20.6% (baseline) to 35.6% (designated time early AM 100%).
Table 5.
Simulation results of visit cycle time and patient wait time for doctor under different experimental scenarios
| DB Strategy | DB Scenario | Double-Booked Time Slots | Visit Cycle Time (minutes) | Patient Wait Time for Doctor (minutes) | |||
|---|---|---|---|---|---|---|---|
| N* | %** | Mean | SD | Mean | SD | ||
| No DB | Baseline | 0 | 0.0 | 71.1 | 28.7 | 14.4 | 21.3 |
| Prediction-Based | 0.8 | 35 | 3.6 | 72.3 | 29.9 | 15.2 | 22.0 |
| 0.7 | 62 | 6.8 | 73.8 | 30.1 | 16.7 | 23.4 | |
| 0.6 | 90 | 9.9 | 75.1 | 30.7 | 18.1 | 24.6 | |
| 0.5 | 125 | 13.6 | 77.9 | 32.4 | 20.4 | 26.8 | |
| 0.4 | 185 | 19.8 | 80.4 | 34.5 | 23.4 | 29.5 | |
| 0.3 | 273 | 28.9 | 85.7 | 37.4 | 28.3 | 33.3 | |
| Random | 5% | 30 | 3.1 | 72.9 | 29.4 | 16.4 | 23.2 |
| 10% | 83 | 8.6 | 75.6 | 30.6 | 18.8 | 24.3 | |
| 15% | 107 | 11.1 | 77.5 | 32.6 | 21.2 | 27.2 | |
| 20% | 158 | 16.4 | 80.7 | 33.1 | 23.6 | 27.9 | |
| 25% | 188 | 19.5 | 84.6 | 36.4 | 27.3 | 31.1 | |
| 30% | 223 | 23.1 | 85.6 | 35.1 | 28.1 | 31.0 | |
| Designated Time (Early AM) | 10% | 19 | 2.0 | 74.8 | 31.5 | 17.1 | 24.6 |
| 30% | 56 | 6.1 | 78.7 | 35.5 | 19.1 | 25.2 | |
| 50% | 94 | 10.2 | 83.0 | 34.0 | 23.3 | 28.4 | |
| 70% | 131 | 14.3 | 88.5 | 38.7 | 27.5 | 33.2 | |
| 90% | 168 | 18.4 | 94.5 | 43.6 | 32.7 | 38.9 | |
| 100% | 187 | 20.4 | 96.4 | 45.0 | 34.5 | 40.4 | |
| Designated Time (Early PM) | 10% | 12 | 1.2 | 71.6 | 29.2 | 14.8 | 21.9 |
| 30% | 36 | 3.6 | 73.9 | 32.8 | 16.2 | 23.3 | |
| 50% | 60 | 6.0 | 74.2 | 31.3 | 17.6 | 24.9 | |
| 70% | 83 | 8.4 | 76.1 | 31.1 | 18.3 | 24.7 | |
| 90% | 107 | 10.7 | 78.3 | 33.0 | 21.0 | 27.4 | |
| 100% | 119 | 11.9 | 79.0 | 33.7 | 21.2 | 27.9 | |
N = Total number of double-booked time slots during the study week.
% = N/Total number of available time slots during the study week.
Overall, the prediction-based DB strategy produced better clinic efficiency compared to other strategies. Three pairs of the experimental scenarios were selected as examples for evaluations of these strategies. In each pair, a prediction-based scenario was compared against another one that was either the random or the designated time scenario. To enable a comparable basis, individual pairs were selected only from those scenarios that had at a similar DB level in terms of the number of double-booked appointments. Figure 4(a) and 4(b) show the comparisons of PWTD and VCT, respectively, based on the three selected pairs of DB scenarios.
Figure 4(a).
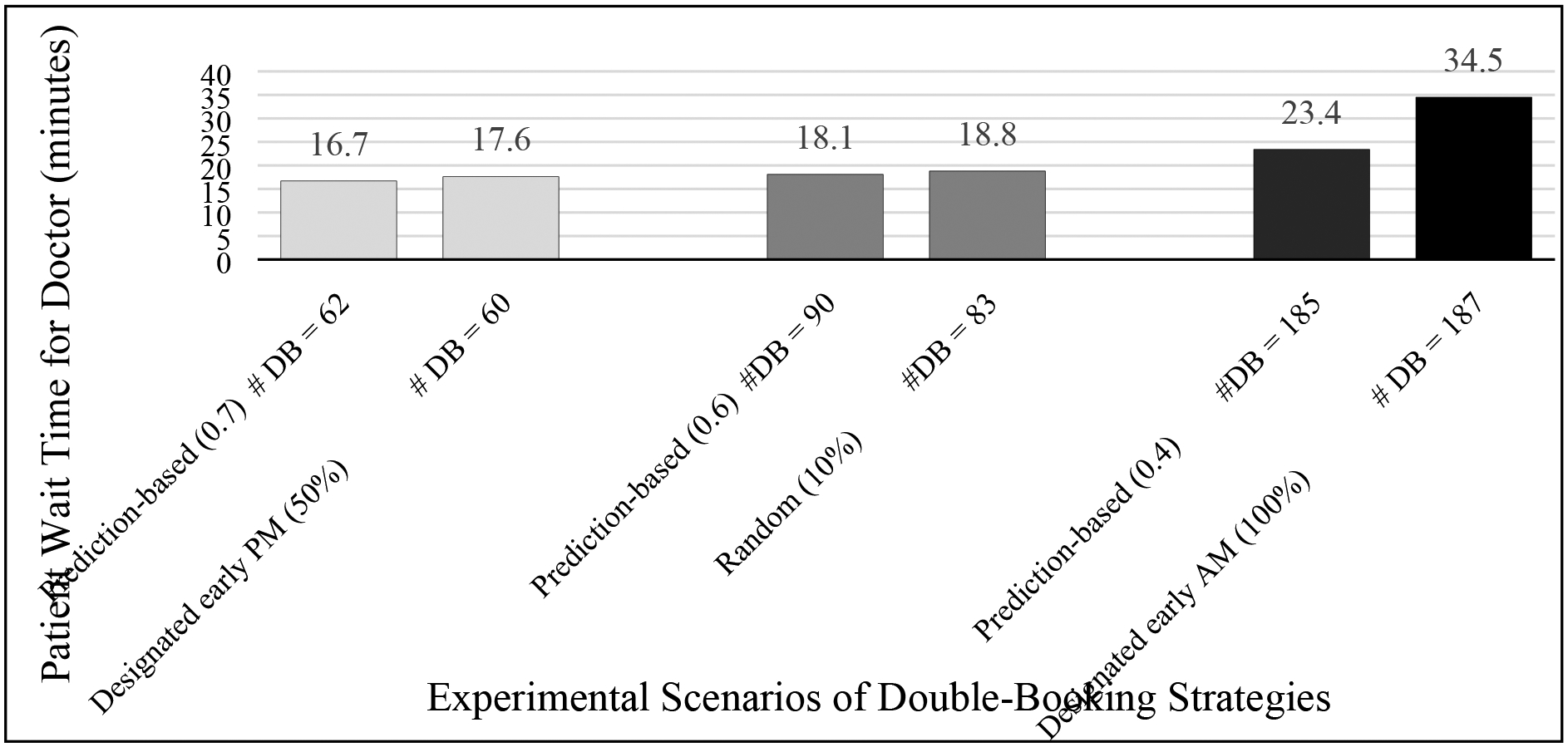
Patient wait time for doctor of selected experimental scenarios under different double-booking strategies (prediction-based vs. random/designated time)
Figure 4(b).

Visit cycle time of selected experimental scenarios under different double-booking strategies (prediction-based vs. random/designated time)
The clinic productivity was expected to be maintained or increased via double-booking. When evaluating DB strategies using the clinic productivity, their impacts were generally consistent and intuitive: the daily clinic throughput (DCT) increased as the number of double-booked appointments increased. However, such increase could potentially result in prolonged VCT and PWTD (as well as overtime of doctors and staff). Hence, it would be more meaningful to analyze the productivity-efficiency trade-offs to enable a more thorough understanding of the DB strategies’ effectiveness. The trade-off analysis was conducted using the percentage increase in DCT versus the percentage increase in VCT (see Figure 5). These two metrics were derived by normalizing DCT and VCT derived from each DB scenario against the corresponding metrics derived from the baseline scenario, respectively. For the same percentage increase in DCT, the prediction-based strategy resulted in the least increase in VCT (i.e., lowest negative impact on efficiency), followed by the random and designated PM strategies. In contrast, the VCT had the greatest increase under the designated AM strategy (i.e., highest negative impact on efficiency).
Figure 5.
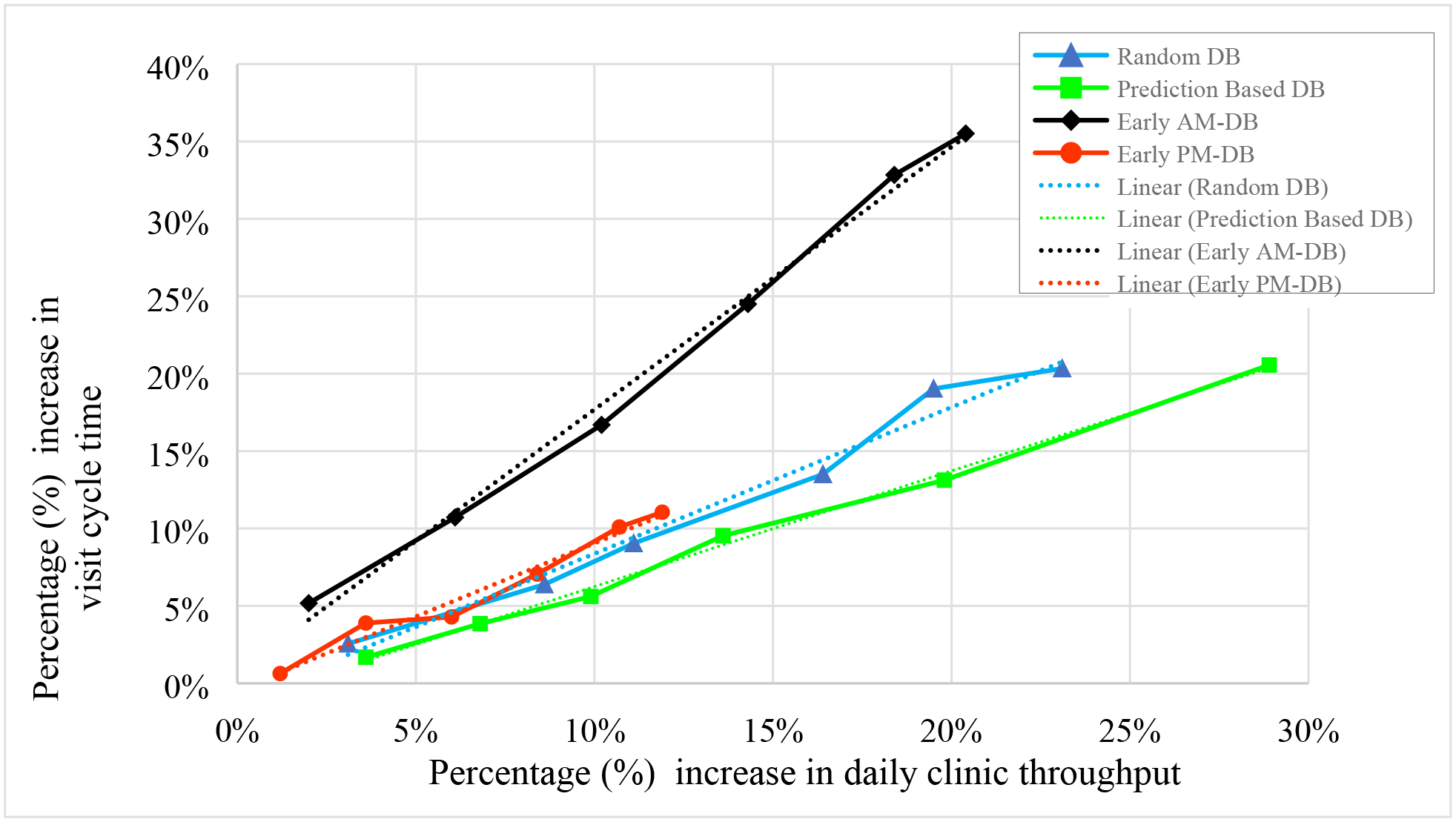
Trade-offs between visit cycle time and clinic throughput under different double-booking strategies
A linear regression analysis was conducted to further examine the statistical significance of these strategies. The outcome variable was the VCT, and the predictor variables were the percentage of increase in DCT and a dummy variable created to denote the DB strategies (reference was the baseline scenario). Table 6 shows the regression results. The DCT increase was found to be a significant factor contributing to the longer VCT. For instance. For instance, an 10% DCT increase (equivalent to 20 additional patient visits per day) would increase VCT by 5.1% (74.7 minutes), 8.0% (76.8), 9.3% (77.7), and 18.9% (84.6) in prediction-based, random, designated PM, and designated AM strategies, respectively, compared to the baseline scenario. The VCTs derived from the prediction-based and designated AM strategies were both significantly different from that derived from the baseline (p-values < 0.001), the prior one was negatively associated (coefficient = −3.809) and the latter one was positively associated (coefficient = 6.001). No evidence showed that the impacts of random and designated PM strategies were significantly different from the baseline scenarios.
Table 6.
Regression analysis results
| Coefficient | Standar d Error | t-statistic | p-value | 95% CI | ||
|---|---|---|---|---|---|---|
| Lower | Upper | |||||
| Constant | 71.1045 | 0.799 | 88.971 | 0.000 | 69.530 | 71.041 |
| Clinic throughput (% increase) | 0.7443 | 0.025 | 30.142 | 0.000 | 0.696 | 0.793 |
| Strategy (dummy) | ||||||
| Prediction-based | − 3.8092 | 0.928 | − 4.106 | 0.000 | − 5.637 | 1.982 |
| Random | − 1.7542 | 0.927 | − 1.893 | 0.060 | − 1.933 | 0.071 |
| Designated AM | 6.0009 | 0.912 | 6.581 | 0.000 | 4.205 | 7.797 |
| Designated PM | − 0.8002 | 0.880 | − 0.909 | 0.364 | − 2.534 | 0.934 |
4.5. Management Implications
The case study demonstrated that the prediction-based double-booking strategy outperformed the other strategies in balancing the impacts of patient no-shows, i.e., clinic productivity and efficiency. The trade-offs analysis showed that, to achieve the same level of daily clinic throughput, using the prediction-based strategy could save 2.1 (2.3), 3.0 (2.4), and 9.8 (6.5) minutes in visit cycle time (patient wait time for doctor) on average comparing to the random, designated PM, and designated AM strategy, respectively. Further, the productivity-efficiency trade-offs at various experimental scenarios under the prediction-based strategy could help clinic administrators determine the best double-booking tactics towards achieving the clinic’s efficiency and productivity goals. Often, some benchmark values (e.g., averaged performances of other similar clinics) can be used to evaluate these trade-offs in determining the most appropriate tactics for a specific clinic. This case study examined six prediction-based scenarios, based on which the increase in clinic throughput ranged from 8 to 56 per day, and the corresponding visit cycle time and patient wait time for doctor increased from 72.3 to 85.7 minutes and from 15.2 to 28.3 minutes, respectively. The benchmark values used in this study were the clinic’s performance outcomes derived under the “expected” operation (i.e., baseline scenario), where each doctor’s appointment was scheduled for exactly one patient, and both double-booking and patient no-show were not present. In the baseline scenario, the average visit cycle time and patient wait time for doctor were found to be 83.3 and 24.6 minutes, respectively. It was found that the prediction-based strategy using the cut-off value of 0.4 generated similar efficiency performance (80.4 and 23.4 minutes), however, the daily clinic throughput could be increased by 20% (i.e., about 39 double-booked time slots per day).
Although the case study focused on the impacts of double-booking on clinic productivity and efficiency, the proposed predictive decision analytics approach based on the hybrid prediction and simulation modeling can be generalized to understand and tackle a range of decision problems involved in primary care operations. Clinic administrators could also use this approach to project the impacts of operational policies and strategies on patient appointment scheduling, patient cancellations and late arrivals, staffing and capacity planning of other resources (e.g., use of exam rooms). Further, this approach could be used to support decision-making under the extreme cases, such as pandemics, when the primary care operations were disrupted by the pandemic policies/interventions, staff shortage, etc. Furthermore, it is worthwhile mentioning that the implementation of the recommended double-booking strategy in real-world settings must be planned and executed with cautions due to the issues/challenges in practice (e.g., what are technologies/tools needed for implementing the strategy on a regular basis, how to implement those technologies/tools with minimal interruptions to the current clinic’s operations), future studies are needed to address those implementation issues.
4.6. Limitations
There are three major limitations in the current study. First, due to the large variations across different primary care clinics (e.g., large public clinic vs. small private clinic), the model design of the proposed approach presented for predictive analytics and simulation modeling cannot capture all the unique characteristics of individual clinics and their specific needs in decision-making. Indeed, the intent of developing this design was to provide a high-level modeling structure that could help guide the detailed model design. Second, as the main purpose of our case study was to demonstrate an application of the proposed approach, the clinic operation was simplified in the current simulation model. For instance, some details in the clinic operation such as nurses’ team behavior and doctors’ EHR documentation activity were not simulated explicitly. Third, while several double-booking strategies were examined in the case study, there are other policies and interventions that hold great promises for patient no-show management, such as open access scheduling policy (i.e., schedule appointments based on patients’ preferences). Future research is needed to address these limitations and provide more comprehensive and valuable information for better patient no-show management and clinic’s operational decision-making in a broader context.
5. Conclusions
The current study develops a predictive decision analytics approach based on hybrid modeling of predictive analytics and simulation modeling to enable predictive decision-making in primary care operations. Comparing to the existing literature typically using a single analytical approach, this approach allows us to develop more effective interventions for primary care operations improvement via linking predictive analytics to simulation modeling and decision evaluation. The use of combined agent-based and discrete-event simulation model to mimic primary care operations also improves the representativeness and granularity of the simulation model, therefore providing a more realistic platform for evaluating various decisions. An application of the proposed approach was presented by a case study conducted in a real family medicine clinic to demonstrate the design and evaluation of double-booking strategies. Based on the model results, a trade-off analysis was conducted between the clinic productivity and efficiency measures, which provided more comprehensive insights of the effectiveness of the studied double-booking strategies. As expected, the prediction-based strategy exceled the random and designated time strategies by achieving the best productivity-efficiency balance. This finding implies a great potential of using the proposed approach to improve primary care operations based on decision-making informed through collective use of predictive analytics, simulation modeling, and decision evaluation.
Highlights.
Prediction is linked to simulation for predicted decision-making in primary care
The predictive decision analytics approach enables more effective decision-making
Trade-offs of primary care measures provide more insights for decision evaluations
Prediction-based double-booking strategy helps achieve better no-show management
Acknowledgments
This project was supported by grant number R18HS027277 from the Agency for Healthcare Research and Quality. The content is solely the responsibility of the authors and does not necessarily represent the official views of the Agency for Healthcare Research and Quality. We thank all the clinic staff and patient subjects for their voluntary participation in this study. We also thank Dr. Kathryn Daniel, Jennifer Roye and Noah Hendrix who provided the research team great clinic expertise and administrative support.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of Interest
Per UTA policy, the following statement is included: Dr. Kay-Yut Chen, has a potential research conflict of interest due to a financial interest with companies Hewlett-Packard Enterprise, Boostr and DecisionNext. A management plan has been created to preserve objectivity in research in accordance with UTA policy.
Credit Author Statement
Yuan Zhou: Conceptualization, Methodology, Software, Validation, Investigation, Writing – Original
Draft, Visualization, Supervision
Amith Viswanatha: Formal analysis, Investigation, Writing – Original Draft, Visualization
Ammar Abdul Motaleb: Investigation, Writing – Original Draft
Prabin Lamichhane: Software, Investigation
Kay-Yut Chen: Writing – Review & Editing, Supervision
Richard Young: Resources, Writing – Review & Editing
Ayse P Gurses: Writing – Review & Editing
Yan Xiao: Writing – Original Draft, Supervision, Project administration, Funding acquisition
Contributor Information
Yuan Zhou, Department of Industrial, Manufacturing, and Systems Engineering, The University of Texas at Arlington, Arlington, Texas, USA.
Amith Viswanatha, Department of Industrial, Manufacturing, and Systems Engineering, The University of Texas at Arlington, Arlington, Texas, USA.
Ammar Abdul Motaleb, Department of Industrial, Manufacturing, and Systems Engineering, The University of Texas at Arlington, Arlington, Texas, USA.
Prabin Lamichhane, Department of Computer Science and Engineering, The University of Texas at Arlington, Arlington, Texas, USA.
Kay-Yut Chen, College of Business, The University of Texas at Arlington, Arlington, Texas, USA.
Richard Young, John Peter Smith Family Medicine Residency Program, Fort Worth, Texas, USA.
Ayse P Gurses, Armstrong Institute Center for Health Care Human Factors, Anesthesiology and Critical Care, Emergency Medicine, and Health Sciences Informatics, School of Medicine, Health Policy and Management, Bloomberg School of Public Health, Malone Center for Engineering in Healthcare, Whiting School of Engineering, Johns Hopkins University, Baltimore, Maryland, USA.
Yan Xiao, College of Nursing and Health Innovation, The University of Texas at Arlington, Arlington, Texas, USA.
References
- [1].Starfield B (1992) Primary care: concept, evaluation, and policy. New York: Oxford University Press. [Google Scholar]
- [2].Jimenez G, Matchar D, Koh G, Tyagi S, Van der Kleij R, Chavannes N, & Car J (2021). Revisiting the four core functions (4Cs) of primary care: Operational definitions and complexities. Primary Health Care Research & Development, 22, E68. 10.1017/S1463423621000669 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Chang CH, Stukel TA, Flood AB, & Goodman DC (2011). Primary care physician workforce and Medicare beneficiaries’ health outcomes. Jama, 305(20), 2096–2104. 10.1001/jama.2011.665 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Shi L (2012). The impact of primary care: a focused review. Scientifica, 2012. 10.6064/2012/432892 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Starfield B, Shi L, & Macinko J (2005). Contribution of primary care to health systems and health. The milbank quarterly, 83(3), 457–502. 10.1111/j.1468-0009.2005.00409.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Kravet SJ, Shore AD, Miller R, Green GB, Kolodner K, & Wright SM (2008). Health care utilization and the proportion of primary care physicians. The American journal of medicine, 121(2), 142–148. 10.1016/j.amjmed.2007.10.021 [DOI] [PubMed] [Google Scholar]
- [7].Shi J, Peng Y, & Erdem E (2014). Simulation analysis on patient visit efficiency of a typical VA primary care clinic with complex characteristics. Simulation Modelling Practice and Theory, 47, 165–181. 10.1016/j.simpat.2014.06.003 [DOI] [Google Scholar]
- [8].Faridimehr S, Venkatachalam S, & Chinnam RB (2019). Managing access to primary care clinics using robust scheduling templates. arXiv preprint arXiv:1911.05129. 10.48550/arXiv.1911.05129 [DOI] [PubMed] [Google Scholar]
- [9].Chand S, Moskowitz H, Norris JB, Shade S, & Willis DR (2009). Improving patient flow at an outpatient clinic: study of sources of variability and improvement factors. Health care management science, 12(3), 325–340. 10.1007/s10729-008-9094-3 [DOI] [PubMed] [Google Scholar]
- [10].Huang YL (2016). The development of patient scheduling groups for an effective appointment system. Applied clinical informatics, 7(01), 43–58. 10.4338/ACI-2015-08-RA-0097 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Kang J, Hanif M, Mirza E, Khan MA, & Malik M (2021). Machine learning in primary care: potential to improve public health. Journal of Medical Engineering & Technology, 45(1), 75–80. [DOI] [PubMed] [Google Scholar]
- [12].Yang Z, Silcox C, Sendak M, Rose S, Rehkopf D, Phillips R, … & Bazemore A (2022, March). Advancing primary care with Artificial Intelligence and Machine Learning. In Healthcare (Vol. 10, No. 1, p. 100594). Elsevier. [DOI] [PubMed] [Google Scholar]
- [13].Kheirkhah P, Feng Q, Travis LM, Tavakoli-Tabasi S, & Sharafkhaneh A (2015). Prevalence, predictors and economic consequences of no-shows. BMC health services research, 16(1), 1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Watson J, Salisbury C, Banks J, Whiting P, & Hamilton W (2019). Predictive value of inflammatory markers for cancer diagnosis in primary care: a prospective cohort study using electronic health records. British journal of cancer, 120(11), 1045–1051. 10.1038/s41416-019-0458-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Ellis DA, McQueenie R, McConnachie A, Wilson P, & Williamson AE (2017). Demographic and practice factors predicting repeated non-attendance in primary care: a national retrospective cohort analysis. The Lancet Public Health, 2(12), e551–e559. 10.1016/S2468-2667(17)30217-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].d’Etienne JP, Zhou Y, Kan C, Shaikh S, Ho AF, Suley E, … & Wang H (2021). Two-step predictive model for early detection of emergency department patients with prolonged stay and its management implications. The American Journal of Emergency Medicine, 40, 148–158. 10.1016/j.ajem.2020.01.050 [DOI] [PubMed] [Google Scholar]
- [17].Futoma J, Morris J, & Lucas J (2015). A comparison of models for predicting early hospital readmissions. Journal of biomedical informatics, 56, 229–238. [DOI] [PubMed] [Google Scholar]
- [18].AlMuhaideb S, Alswailem O, Alsubaie N, Ferwana I, & Alnajem A (2019). Prediction of hospital no-show appointments through artificial intelligence algorithms. Annals of Saudi medicine, 39(6), 373–381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Zhu K, Lou Z, Zhou J, Ballester N, Kong N, & Parikh P (2015). Predicting 30-day hospital readmission with publicly available administrative database. Methods of information in medicine, 54(06), 560–567. [DOI] [PubMed] [Google Scholar]
- [20].Mekhaldi RN, Caulier P, Chaabane S, Chraibi A, & Piechowiak S (2020, April). Using machine learning models to predict the length of stay in a hospital setting. In World Conference on Information Systems and Technologies (pp. 202–211). Springer, Cham. [Google Scholar]
- [21].Elbattah M, & Molloy O (2016, September). Using machine learning to predict length of stay and discharge destination for hip-fracture patients. In Proceedings of SAI intelligent systems conference (pp. 207–217). Springer, Cham. [Google Scholar]
- [22].Mohnen SM, Rotteveel AH, Doornbos G, & Polder JJ (2020). Healthcare expenditure prediction with neighbourhood variables–a random forest model. Statistics, Politics and Policy, 11(2), 111–138. [Google Scholar]
- [23].Turgeman L, & May JH (2016). A mixed-ensemble model for hospital readmission. Artificial intelligence in medicine, 72, 72–82. [DOI] [PubMed] [Google Scholar]
- [24].Carreras-García D, Delgado-Gómez D, Llorente-Fernández F, & Arribas-Gil A (2020). Patient no-show prediction: A systematic literature review. Entropy, 22(6), 675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Brailsford SC (2007, December). Tutorial: Advances and challenges in healthcare simulation modeling. In 2007 Winter Simulation Conference (pp. 1436–1448). IEEE. 10.1109/WSC.2007.4419754 [DOI] [Google Scholar]
- [26].Mustafee N, Katsaliaki K, & Taylor SJ (2010). Profiling literature in healthcare simulation. Simulation, 86(8–9), 543–558. 10.1177/0037549709359090 [DOI] [Google Scholar]
- [27].Davahli MR, Karwowski W, & Taiar R (2020). A system dynamics simulation applied to healthcare: A systematic review. International journal of environmental research and public health, 17(16), 5741. 10.3390/ijerph17165741 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Atun RA, Lebcir RM, McKee M, Habicht J, & Coker RJ (2007). Impact of joined-up HIV harm reduction and multidrug resistant tuberculosis control programmes in Estonia: system dynamics simulation model. Health Policy, 81(2–3), 207–217. 10.1016/j.healthpol.2006.05.021 [DOI] [PubMed] [Google Scholar]
- [29].Lebcir RM, Atun RA, & Coker RJ (2010). System dynamic simulation of treatment policies to address colliding epidemics of tuberculosis, drug resistant tuberculosis and injecting drug users driven HIV in Russia. Journal of the Operational Research Society, 61(8), 1238–1248. 10.1057/jors.2009.90 [DOI] [Google Scholar]
- [30].Arboleda CA, Abraham DM, & Lubitz R (2007). Simulation as a tool to assess the vulnerability of the operation of a health care facility. Journal of performance of constructed facilities, 21(4), 302–312. 10.1061/(ASCE)0887-3828(2007)21:4(302) [DOI] [Google Scholar]
- [31].Ahmad S (2005). Closing the youth access gap: the projected health benefits and cost savings of a national policy to raise the legal smoking age to 21 in the United States. Health Policy, 75(1), 74–84. 10.1016/j.healthpol.2005.02.004 [DOI] [PubMed] [Google Scholar]
- [32].Harper PR, & Gamlin HM (2003). Reduced outpatient waiting times with improved appointment scheduling: a simulation modelling approach. Or Spectrum, 25(2), 207–222. 10.1007/s00291-003-0122-x [DOI] [Google Scholar]
- [33].Ogulata SN, Cetik MO, Koyuncu E, & Koyuncu M (2009). A simulation approach for scheduling patients in the department of radiation oncology. Journal of medical systems, 33(3), 233–239. 10.1007/s10916-008-9184-2 [DOI] [PubMed] [Google Scholar]
- [34].Swisher JR, & Jacobson SH (2002). Evaluating the design of a family practice healthcare clinic using discrete-event simulation. Health Care Management Science, 5(2), 75–88. 10.1023/A:1014464529565 [DOI] [PubMed] [Google Scholar]
- [35].Hamrock E, Paige K, Parks J, Scheulen J, & Levin S (2013). Discrete event simulation for healthcare organizations: a tool for decision making. Journal of Healthcare Management, 58(2), 110–124. http://www.ncbi.nlm.nih.gov/pubmed/23650696. [PubMed] [Google Scholar]
- [36].Parks JK, Engblom P, Hamrock E, Satjapot S, & Levin S (2011). Designed to fail: how computer simulation can detect fundamental flaws in clinic flow. Journal of Healthcare Management, 56(2), 135–146. https://pubmed.ncbi.nlm.nih.gov/21495531. [PubMed] [Google Scholar]
- [37].Zhu Z (2011). Impact of different discharge patterns on bed occupancy rate and bed waiting time: a simulation approach. Journal of medical engineering & technology, 35(6–7), 338–343. 10.3109/03091902.2011.595528 [DOI] [PubMed] [Google Scholar]
- [38].Zhou Y, Ancker JS, Upahdye M, McGeorge NM, Guarrera TK, Hedge S, … & Lin L (2014). The impact of interoperability of electronic health records on ambulatory physician practices: a discrete-event simulation study. Journal of Innovation in Health Informatics, 21(1), 21–29. https://pubmed.ncbi.nlm.nih.gov/24629653. [DOI] [PubMed] [Google Scholar]
- [39].Katsaliaki K, & Mustafee N (2016). Applications of simulation within the healthcare context. In Operational research for emergency planning in healthcare: volume 2 (pp. 252–295). Palgrave Macmillan, London. 10.1007/978-1-137-57328-5_12 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Abdelghany M, & Eltawil AB (2017). Linking approaches for multi-methods simulation in healthcare systems planning and management. International Journal of Industrial and Systems Engineering, 26(2), 275–290. 10.1504/IJISE.2017.083676 [DOI] [Google Scholar]
- [41].Macal C, & North M (2014, December). Introductory tutorial: Agent-based modeling and simulation. In Proceedings of the winter simulation conference 2014 (pp. 6–20). IEEE. 10.1109/WSC.2014.7019874 [DOI] [Google Scholar]
- [42].Taboada M, Cabrera E, Epelde F, Iglesias ML, & Luque E (2013). Using an agent-based simulation for predicting the effects of patients derivation policies in emergency departments. Procedia Computer Science, 18, 641–650. 10.1016/j.procs.2013.05.228 [DOI] [Google Scholar]
- [43].Wang L (2009, April). An agent-based simulation for workflow in emergency department. In 2009 Systems and Information Engineering Design Symposium (pp. 19–23). IEEE. 10.1109/SIEDS.2009.5166148 [DOI] [Google Scholar]
- [44].Laskowski M, & Mukhi S (2008, September). Agent-based simulation of emergency departments with patient diversion. In International Conference on Electronic Healthcare (pp. 25–37). Springer, Berlin, Heidelberg. 10.1007/978-3-642-00413-1_4 [DOI] [Google Scholar]
- [45].Kaushal A, Zhao Y, Peng Q, Strome T, Weldon E, Zhang M, & Chochinov A (2015). Evaluation of fast track strategies using agent-based simulation modeling to reduce waiting time in a hospital emergency department. Socio-Economic Planning Sciences, 50, 18–31. 10.1016/j.seps.2015.02.002 [DOI] [Google Scholar]
- [46].Dos Santos VH, Kotiadis K, & Scaparra MP (2020, December). A review of hybrid simulation in healthcare. In 2020 Winter Simulation Conference (WSC) (pp. 1004–1015). IEEE. 10.1109/WSC48552.2020.9383913 [DOI] [Google Scholar]
- [47].Viana J, Brailsford SC, Harindra V, & Harper PR (2014). Combining discrete-event simulation and system dynamics in a healthcare setting: A composite model for Chlamydia infection. European Journal of Operational Research, 237(1), 196–206. 10.1016/j.ejor.2014.02.052 [DOI] [Google Scholar]
- [48].Tejada JJ, Ivy JS, King RE, Wilson JR, Ballan MJ, Kay MG, … & Yankaskas BC (2014). Combined DES/SD model of breast cancer screening for older women, II: screening-and-treatment simulation. IIE transactions, 46(7), 707–727. 10.1080/0740817X.2013.851436 [DOI] [Google Scholar]
- [49].Anagnostou A, Nouman A, & Taylor SJ (2013, December). Distributed hybrid agent-based discrete event emergency medical services simulation. In 2013 Winter Simulations Conference (WSC) (pp. 1625–1636). IEEE. 10.1109/WSC.2013.6721545 [DOI] [Google Scholar]
- [50].Chen Y, Kuo YH, Balasubramanian H, & Wen C (2015, December). Using simulation to examine appointment overbooking schemes for a medical imaging center. In 2015 Winter Simulation Conference (WSC) (pp. 1307–1318). IEEE. [Google Scholar]
- [51].Ho TW, Kung LC, Huang HY, Lai JF, & Chiu HM (2021). Overbooking for physical examination considering late cancellation and set-resource relationship. BMC Health Services Research, 21(1), 1–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Wang C, Deng L, & Zhou W (2022). “We Missed You!”: A Joint Optimization Strategy of Appointment Window and Reminder Sending. Computers & Industrial Engineering, 108198. [Google Scholar]
- [53].Xie X, Fan Z, & Zhong X (2021). Appointment Capacity Planning With Overbooking for Outpatient Clinics With Patient No-Shows. IEEE Transactions on Automation Science and Engineering, 19(2), 864–883. [Google Scholar]
- [54].Zeng B, Turkcan A, Lin J, & Lawley M (2010). Clinic scheduling models with overbooking for patients with heterogeneous no-show probabilities. Annals of Operations Research, 178(1), 121–144. [Google Scholar]
- [55].Chen Y, Kuo YH, Fan P, & Balasubramanian H (2018). Appointment overbooking with different time slot structures. Computers & Industrial Engineering, 124, 237–248. [Google Scholar]
- [56].Kuo YH, Balasubramanian H, & Chen Y (2020). Medical appointment overbooking and optimal scheduling: tradeoffs between schedule efficiency and accessibility to service. Flexible Services and Manufacturing Journal, 32(1), 72–101. [Google Scholar]
- [57].Tolles J, & Meurer WJ (2016). Logistic regression: relating patient characteristics to outcomes. Jama, 316(5), 533–534. [DOI] [PubMed] [Google Scholar]
- [58].Ho TK (1998). The random subspace method for constructing decision forests. IEEE transactions on pattern analysis and machine intelligence, 20(8), 832–844. [Google Scholar]


