Abstract
Patients with type 1 diabetes manually regulate blood glucose concentration by adjusting insulin dosage in response to factors such as carbohydrate intake and exercise intensity. Automated near-term prediction of blood glucose concentration is essential to prevent hyper- and hypoglycaemic events in type 1 diabetes patients and to improve control of blood glucose levels by physicians and patients. The imperfect nature of patient monitoring introduces missing values into all variables that play important roles to predict blood glucose level, necessitating data imputation. In this paper, we investigated the importance of variables and explored various feature engineering methods to predict blood glucose level. Next, we extended our work by developing a new empirical imputation method and investigating the predictive accuracy achieved under different methods to impute missing data. Also, we examined the influence of past signal values on the prediction of blood glucose levels. We reported the relative performance of predictive models in different testing scenarios and different imputation methods. Finally, we found an optimal combination of data imputation methods and built an ensemble model for the reliable prediction of blood glucose levels on a 30-minute horizon.
Electronic supplementary material
The online version of this article (10.1007/s41666-019-00063-2) contains supplementary material, which is available to authorized users.
Keywords: Missing data imputation, Type 1 diabetes, Blood glucose level, Machine learning, Gradient boosted trees
Introduction
Type 1 diabetes (T1D) is a chronic disease in which the pancreas fails to produce insulin to regulate blood glucose (BG) levels [1, 2]. This dysfunction can lead to both hypoglycaemia (low blood sugar) and hyperglycaemia (high blood sugar) and burdens patients to self-regulate carbohydrate consumption and delivery of supplemental insulin. Furthermore, hyperglycaemia can lead to medical complications such as blindness, kidney failure, and amputations and increases risk of heart disease and stroke. Meanwhile, hypoglycaemia can cause acute symptoms such as loss of consciousness, seizures, and even death [3]. In order to avoid such diabetic complications, patients continually monitor their BG levels and adjust insulin doses accordingly. An increasing number of T1D patients are adopting continuous glucose monitoring (CGM) devices and insulin pump therapy, wherein a wearable device releases insulin subcutaneously to mimic pancreatic response. Current insulin pump therapy requires manual approval of each recommended insulin dose which regulates BG levels. Effective prediction of BG levels and diabetic complications before they occur would give patients time to intervene and prevent these BG excursions, thus improving overall health, safety, and quality of life.
Many studies have applied machine-learning and deep-learning techniques to predict BG levels and identify diabetic complications. Bertachi et al. proposed BG level prediction models using artificial neural networks (ANN) and physiological models [1]. Other types of deep-learning algorithms such as convolutional neural network (CNN) [4], recurrent neural network (RNN) [5, 6], and evolutionary search algorithm such as grammatical evolution (GE) model [7] also have been proposed for BG level prediction. Furthermore, CGM measurements combined with machine-learning approaches have been applied to predict real-time hypoglycaemia events in types 1 and 2 diabetes [8, 9] and hyperglycaemia events in type 1 diabetes [10]. Nevertheless, it remains challenging to predict BG levels using CGM and other physiological and clinical data due to the imperfections of patient monitoring and intermittent sampling rates of biosignals [11]. Unexpected malfunction of monitoring devices and unreliable self-reporting causes data gaps, thus limiting the accuracy of predicting future BG levels. Imputing missing values with reasonable estimates and extracting informative features from physiological and self-reported features can improve prediction accuracy of BG levels.
This study is an extension of the work originally reported at the 3rd International Workshop in Knowledge Discovery in Healthcare at IJCAI 2018, in which we explored and compared multiple machine-learning and deep-learning methods to predict BG levels at a 30-minute horizon and found that a gradient-boosted regression tree (XGBoost) model showed the best performance compared to Random Forest and a simple 2-layer LSTM models [12]. Our predictive model achieved competitive performance at the workshop [13]. From the study, we realized that unexpected malfunction of monitoring devices and unreliable self-reporting causes data gaps, thus limiting the accuracy of predicting future BG levels. Furthermore, a key challenge to blood glucose prediction was that not all conventional missing value imputation methods were compatible with online BG level prediction. Specifically, imputation methods that involve both boundary points of the data gap (i.e. interpolation) cannot be used in a realistic online setting, since one boundary point lies in the future. Here, we investigated the importance of physiological and monitoring features with respect to BG level prediction, explored various imputation methods on the training set of each patient in the OhioT1DM cohort, and compared the prediction accuracy on the test set for each imputation method. We measured the accuracy under two distinct conditions: a batch-mode scenario (conventional train-test setting) and an online deployment setting (where future points are unknown). Finally, we chose the five most effective methods for imputing missing data, trained BG level predictors under each imputation method, and built an ensemble model by combining their predictions. The ensemble model outperformed individual predictive models in both conventional and realistic settings.
Methods
Dataset and Preprocessing
The OhioT1DM cohort was used to evaluate imputation methods and build predictive models [14]. The dataset comprised 19 features collected over an 8-week period from 6 people with T1D, as detailed by Marling et al. [15]. The features in the dataset either were self-reported (and recorded intermittently) or were recorded at 5-minute intervals from devices: an insulin pump, continuous glucose monitor, and a fitness band (Supplementary Table 1). We grouped features according to their sampling frequency, denoting one-off features as signals that were recorded intermittently with no fixed sampling frequency and quasi-continuous features as signals that were continuously monitored and aggregated at 5-minute intervals. One-off features included finger-stick glucose, insulin bolus time and dose, sleep times and quality, work intensity, exercise intensity and duration, meal type and carbohydrate content, hypoglycaemic events, illnesses, and stressors. Quasi-continuous features included continuous glucose monitor (CGM) glucose level, basal and temporary basal rates of insulin infusion, heart rate, steps taken, galvanic skin response, skin temperature, and air temperature. Due to intermittent measurements with no fixed measuring frequency or duration of one-off features and occasional missing values, the feature vector at any given timestamp was not guaranteed to contain values for all fields. Therefore, we resampled our data to 5-minute intervals, reflecting the 5-minute aggregation frequency of the quasi-continuous variables, and realigned each resampled series to the nearest multiple of 5 minutes. Within each 5-minute resampling window, we then aggregated each feature using the mean within the last 5 minutes for quasi-continuous features, the last valid value for one-off features and the maximum value within the last 5 minutes for finger-stick glucose to capture probable diabetes signal. We assumed that missing values (or rather, unavailable values) in work intensity, exercise intensity, sleep quality, illness, stressors, hypoglycaemic events, and meals represented the true absence of these signals (e.g. wakefulness and non-illness) and filled data gaps in these variables with zeros. Two separated datasets were provided by IJCAI 2018 challenge organizers. One was for the training (first 46 days of record), and the other was for the testing (last 10 days of record). This longitudinal dataset enabled us to measure the accuracy of blood glucose level prediction using measuring root mean square error (RMSE), mean absolute error (MAE), and Pearson’s correlation coefficient (PCC).
Feature Engineering, Feature Expansion, and Dataset Generation
Starting with 19 variables including CGM-monitored glucose levels (as provided by the OhioT1DM dataset), we expanded our feature set by adding missing value indicators, lagged-time features, time indicators, and glucose-related features. Missing value indicators represented the presence or absence of missing values in 14 features (e.g. 1 = observed value; 0 = missing value that was imputed). It has been shown that missing value indicator helped to improve prediction performance for multivariate time series [16]. For time-lagged features, we generated 12 lagged versions of each feature (lagged at 5-minute intervals up to 1 hour before the current timestamp, in total 216 features). We did not generate lagged versions of stressors, illness, and hypoglycaemic events, since these occurred infrequently. The 31 time indicators represented day of week (7 days) and time of day (24 hours). We also generated glucose-related features (e.g. differences of glucose levels between timestamps and finger-stick glucose level since last measurement) as described previously [12]. In total, we derived a feature set consisting of 320 features. They were used to select the optimal imputation methods and generate predictive models for BG levels (Supplementary Table 1).
To evaluate the ability of different imputation methods to predict future BG levels and maximize the information content of predictive models, remaining missing values of quasi-continuous features and one-off features were imputed using 16 imputation methods described in Section 2.3. To avoid intervals of intermittent data availability at the start and end of each training and test set, we trimmed each data period to span from 00:00:00 (midnight) on the first full day to 11:55:00 on the last full day. Preprocessed training and test sets were composed of 44 days (mean 12,672 timestamps) and 8 days (mean 2304 timestamps) of record per patients, respectively. To examine the effect of trimmed test sets on prediction accuracies, we also generated untrimmed test sets, which were composed of values that were observed between the first timestamp and last timestamp that CGM values were reported. Prediction accuracies in trimmed and untrimmed test sets were significantly similar (Supplementary Table 2). RMSE measured from trimmed and untrimmed test sets showed PCC of 0.9 (P-value = 2.21 × 10−24). To compare prediction performance across the same range of time points across patients, we reported prediction accuracies on trimmed test sets.
Imputation Methods
Missing values were filled with reasonable values using 11 imputation methods for a time series dataset. Linear interpolation (LI) and spline interpolation (SPI) replace missing data with fitted values from a linear polynomial model and a special type of piecewise polynomial (spline) model [17], respectively. Kalman smoothing with structural model (KS) and Kalman smoothing with auto-ARIMA model (KA) estimate a joint probability distribution over the variables for each timeframe and produce estimates of missing data. For the estimation, KS used a structural model fitted by maximum likelihood and KA used the state space representation of ARIMA model [18]. Moving average (MA) fills missing data using the moving average computed over four timestamps. Average of all observed values (mean) and randomly selected values (random) were also used for imputation. All of the imputation methods mentioned above were implemented using the R package imputeTS (v. 2.7) [19]. Stineman interpolation (STI), which replaces missing data using Stineman’s algorithm-based piecewise rational function [20], last observed carried forward (LOCF), and k-nearest neighbour (KNN) methods were implemented using stinepack (v. 1.4) [21], zoo (v. 1.8.4) [22], and fancyimpute (v. 0.5.2) [23], respectively. KNN finds the K closest neighbours for missing data from observed data [24]. For KNN imputation, we tested 2 (KNN-2), 4 (KNN-4), 6 (KNN-6), 8 (KNN-8), and 10 (KNN-10) nearest neighbours.
In addition to the methods listed above, we developed an empirical imputation method (Emp) which filled a given data gap with values from the training set, observed at the same timestamps as the data gap. For each missing value timestamp, we collected all values from the training set observed within ±5 minutes of the missing value’s timestamp. This gives us the historical distribution of observed feature values for a 10-minute time period, within which the missing test value is encountered. Given this temporally constrained empirical distribution of feature values, we imputed the missing value with either the mean of the distribution (Emp-mean) or a randomly chosen value (Emp-random) from the distribution. For example, we collected all observed values between 2:30 pm and 2:40 pm of each day in a training set and assigned the average value to a data gap at 2:35 pm. In total, we tested 16 imputation methods (Table 1).
Table 1.
Implemented imputation methods
| Method | Abbreviation | Additional scheme | Description |
|---|---|---|---|
| Linear interpolation | LI | - | Line fit between end points |
| Spline interpolation | SPI | - | Spline curve fit between end points of missing data gap |
| Stineman interpolation | STI | - | Stineman cubic curve fit between end points of missing data gap |
| Kalman smoothing with structural model | KS | - | Kalman smoothing using a structural model fitted by maximum likelihood estimated |
| Kalman smoothing with auto-ARIMA model | KA | - | Kalman smoothing using the state space representation of ARIMA model |
| Last observed carried forward | LOCF | - | Missing values are replaced with last observed values |
| Average value based imputation | Mean | - | Missing values are replaced with average of all observed values |
| Moving average | MA | - | Missing data filled in using the moving average computed over four timestamps |
| K-nearest neighbours | KNN | KNN-2, KNN-4, KNN-6, KNN-8, and KNN-10 | Missing values are replaced with the K-nearest neighbours for missing values from observed values. 2, 4, 6, 8, and 10 nearest neighbours are considered for imputation. |
| Empirical imputation | Emp | Emp-mean and Emp-random | Observed values within a specific ± 5-minute windows for all days in the training set were collected. Missing values were filled in with the mean (Emp-mean) or selected randomly from the corresponding window’s distribution (Emp-random) |
| Random assignment | Random | - | Randomly selected value from within the feature value range |
Model Training and Evaluation
We generated personalized XGBoost models for BG level prediction, which were specific for individual patients and used all 320 features. XGBoost comprised an ensemble of decision trees, combined in a gradient boosting framework. This model is known for its high predictive performance, robustness to outliers and unbalanced classes, and efficient split finding through parallel training [25]. XGBoost has been broadly applied to various healthcare-related time series forecasting and classification problems, including epilepsy patient identification [26] and sleep stage determination [27]. A prime advantage of using XGBoost is that the importance of each feature that is required to make a prediction can be estimated. This is contrast to deep-learning models, where it can be difficult to interpret why the model made a particular prediction. For the performance evaluation of predictive models, RMSE, MAE, and PCC were computed.
To generate an ensemble model, we selected a set of imputation methods that yielded the best performance to predict BG levels under identical gradient boosting platform. We first trained predictive models using training sets that were imputed by 16 different imputation methods. To examine overall prediction accuracies of imputation methods, we generated a cluster map between imputation methods and three evaluation metrics (RMSE, MAE, and PCC). We then selected one cluster showing higher overall accuracy across all three metrics (i.e. cluster was enriched with low RMSEs, low MAEs, and high PCCs). Next, we measured accuracy variances of seven imputation methods across patients (variances of RMSEs, MAEs, and PCCs across patients). Small variance indicated that a given imputation method achieved high prediction accuracies in all patients. Rank product (geometric mean of accuracy variances) was used to compute an aggregate rank across observed rankings of RMSE variances, MAE variances, and PCC variances. Finally, the top five imputation methods (LOCF, SPI, STI, KS, and LI) were selected based on rank product.
Hyperparameter optimization for these five predictive models was performed to find an optimal set of XGBoost parameters; learning rate (eta), maximum tree depth (max_depth), and loss reduction (gamma), and number of rounds for boosting (num_round). For this, we followed a standard grid-search procedure. Three eta values (0.05, 0.1, and 0.2), three max_depth values (3, 5, and 10), and four gamma values (0, 0.5, 1, and 5) were used to find optimized parameter combination. In total, 36 parameter combinations (3 eta × 3 max_depth × 4 gamma) were generated. For the optimization, we used cross-validation with 10 blocked subsets, a variant of k-fold cross-validation adapted for time series dataset (tenfold blocked cross-validation) [28]. The training set was divided into ten blocks maintaining time ordering (without shuffling). Nine blocks were used to train a model, and one block was used to measure prediction accuracy. Ten resulting RMSEs were averaged using the mean to calculate the final cross-validation RMSE. The number of rounds for boosting was optimized automatically during the cross-validation. We selected the parameter combination showing the lowest cross-validation RMSE to build patient-specific predictive models. The average percent difference in RMSE between the best and worst parameter combination was 9%. We fit the model to the data a1, a2,. . . , at and assume ât + 1 is the predicted next observation. Error was calculated between the actual and predicted values (e*t + 1 = at + 1 – ât + 1). We then repeated fitting step for t = m,. . . , n-1 where m is the minimum number of observations needed for fitting the model and compute the RMSE from e*m + 1…e*n. Five models were built using their optimized parameters, and individual model predicted BG levels at each timestamp. Finally, we averaged the predictions across the five models to get consensus BG level at each timestamp. Additionally, we generated weighted average-based ensemble model and compared prediction performance between two types of ensemble models (general average vs. weighted average). The reverse rank product of each imputation method (1/rank product) is considered as a weight. Two ensemble models showed compatible performance in all three testing scenarios (Supplementary Table 3). The performance of average-based ensemble models was used for further analyses.
For each patient, a model was trained, using the optimal set of parameters, over the entire training set. Next, we generated three types of test sets to simulate both a conventional batch train-test approach and online prediction, where missing values can only be imputed using past data. Of the imputation methods being evaluated, LOCF and Emp-mean support use in an online setting.
Conventional train-test setting (test-full) – Batch: all test points were known beforehand, and predictions were made on the entire test set as a batch. In this setting, all 16 imputation methods were applied for imputing missing values in the test set.
Realistic deployment setting (test-partial) – Online: the temporal order of points in the test set was maintained. The last observed value was carried forward (LOCF) to impute missing values encountered in the test set.
Realistic deployment setting (test-empirical) – Online: given the timestamp of a missing value in the test set, we impute the missing values using Emp-mean.
Statistical Analysis and Data Visualization
To build predictive models, XGBoost (v. 0.81) [25] was used in a Python (v. 3.7.0) environment. SciPy (v. 1.1.0) [29], NumPy (v. 1.15), and scikit-learn (v. 0.21) [30] were used for statistical analyses and measurements of RMSE and MAE. Seaborn (v. 0.9.0) [31] and matplotlib (v. 3.0) were used for data visualization.
Results
Feature Ablation Analysis
To understand the properties of physiological and monitoring features with respect to BG level prediction, we conducted an ablation study. First, 19 variables, which were originally provided by the OhioT1DM dataset, were divided into 4 groups: (1) self-reported features (S; meals, finger-stick glucose, illness, stress, exercise, and work), (2) basis peak band features (B; heart rate, galvanic skin response, skin and air temperature, steps, and sleep), (3) insulin pump features (P; basal and temporary basal infusion rates, bolus doses, and types), and (4) continuous glucose monitoring feature (G; blood glucose level). Next, we generated 15 combinations of the S, P, B and G feature groups, used them to build XGBoost-based predictive models for BG levels, and measured prediction accuracy (Supplementary Table 4). We found that S + G showed slightly better overall prediction performance compared to other feature groups. However, its prediction accuracy was inconsistent across patients (i.e. S + G did not have the smallest variance) suggesting that patients have different routines and styles to report their health condition, and this inevitable and self-biased information would play differentially to predict blood glucose level. Indeed, models trained on S and P, which required manual operation (injecting extra bolus doses), and feature combinations with S or P were likely to have high prediction variance and low prediction accuracy across patients. Meanwhile, models trained on G alone outperformed those without G, and prediction accuracy was likely to be improved when other feature groups were added to G. Taken together, our results indicated that blood glucose level could be affected by physiological signal (B and P) and patient condition (S) though their importance for the prediction would be different depending on patients, and therefore considering all feature groups for subsequent experiments would be helpful to avoid potential loss of information that could improve BG level prediction in a patient-specific manner.
Comparison of Methods for Missing Data Imputation
From the time period of OhioT1DM dataset, we found that, on average, ~ 30% of quasi-continuous feature values and ~ 9% of BG level were missing. Meanwhile, more than 90% values of one-off features were unavailable due to their intermittent measurement. The number of missing values necessitated the use of effective imputation methods of missing values in both quasi-continuous and one-off features to train reliable predictors of BG levels.
We first examined the similarity of imputed values in a training set. Finger-stick glucose level was used for this comparison, since this feature was one of the one-off features showing a large fraction of missing values, and finger sticks provided an accepted standard measurement of BG levels. We imputed missing values for finger-stick glucose level using each of the imputation methods. Then, we computed pairwise RMSEs between the imputed finger-stick values. From hierarchical clustering analysis, we found that certain imputation methods showed similar imputation behaviours (Fig. 1a). Although the order of imputation methods in a cluster is different, there was a set of imputation methods that shared similar imputation profile across patients. For example, KNN-based methods shared similar imputed values regardless of the number of neighbours. Kalman smoothing-based (KS and KA), interpolation-based (LI, SPI, and STI), and moving average-based (MA) methods were likely to generate similar imputation profiles (Supplementary Fig. 1).
Fig. 1.

Imputation profiles of features. Euclidean distance was used to compare the similarity between two variables, and average linkage method was used to calculate clusters and generate cladogram. a Agreement between 16 imputation methods. Blue indicates small RMSE, and light green indicates large RMSE between imputed finger-stick glucose levels, respectively. Comparison of Patient 575 was shown. b Associations between BG levels and imputed feature values. Z-score normalized RMSEs (norm-RMSEs) between BG levels and their imputed counterparts were presented. GSR indicated galvanic skin response. Associations of Patient 575 was shown. c Normalized RMSE between BG levels and finger-stick glucose levels of patients
In addition, we examined the associations between imputed values of each feature and observed BG levels. To do this, we performed z-score-based normalization of BG levels and feature values so that they have similar value range, and measured their relative RMSEs. Individual features showed different levels of associations with BG levels (Fig. 1b and Supplementary Fig. 2). Quasi-continuous features tended to have better associations with BG levels than one-off features except finger-stick glucose level. In fact, finger-stick glucose level showed the strongest association in all patients regardless of imputation methods (Fig. 1c). Meanwhile, one-off features that were composed of binary events (0 = no event and 1 = event; e.g. hypoglycaemia) showed a weak correlation with BG potentially due to the small number of events or limited binary information.
Association Between Lagged-Time-Based Features and Blood Glucose Levels
The continuous glucose monitors used in the OhioT1DM cohort recorded interstitial glucose concentration, which lags behind capillary glucose concentration [32], which in turn takes time to respond to carbohydrate intake, insulin infusion, and physical activity. To understand the lagged associations between BG levels and the features, we generated 12 time-lagged versions of each feature (at 5-minute intervals up to 1 hour before each timestamp) and examined the importance of each time-lagged feature in predicting BG levels at the current timestamp. The feature importance was computed using Random Forest algorithm, which measured how effective the feature was at reducing variance when creating decision trees within Random Forests (the mean decrease in impurity) [33].
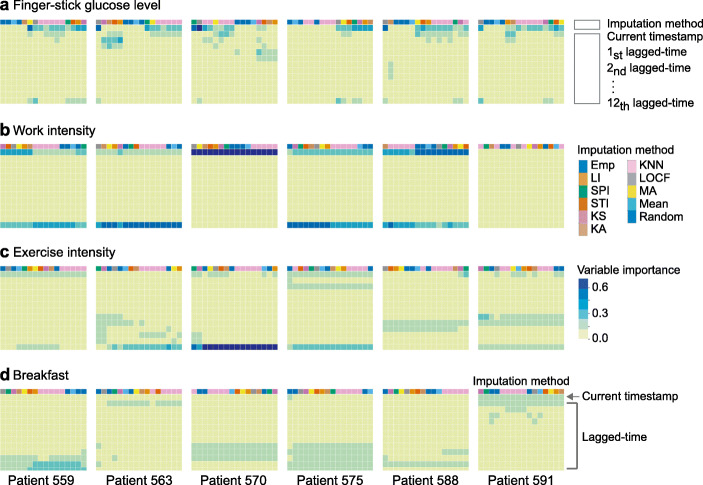
We found that current BG level was associated with different time-lagged features, with the strongest time-lag varying across both patients and features (Fig. 2a). For example, finger-stick glucose level at current timestamp had the highest importance score. Work intensity and exercise intensity both showed high feature importance at the current timestamp as well as 1-hour prior (Fig. 2b and c). Interestingly, breakfast timing affected patients’ BG levels differently. BG levels in patients 559, 570, 575, and 588 were associated with breakfast at larger time lags (up to 1-hour prior), whereas BG levels in patients 563 and 591 were associated with breakfast at more recent time lags, and these patterns persisted across different imputation algorithms (Fig. 2d). These temporal variations were observed across features suggesting that time-lagged features could play an important role in personalized BG level prediction.
Fig. 2.
Feature importance depending on lagged-time points. Importance of a finger-stick glucose level, b work intensity, c exercise intensity, and d breakfast indicator that were imputed by different imputation methods were compared. Y-axis indicated 12 time-lagged versions of a given feature (at 5-minute intervals up to 1 hour before each timestamp). X-axis indicated 16 imputation methods. Blue indicated a given lagged-time was strongly associated with BG levels
Given the considerable variation in predictive importance of features and their temporally lagged values across patients, we extended our feature space to include 12 time-lagged versions for individual features, binary missing value indicators, glucose-related features, and time-related features (see Methods for details). In total, 320 features were generated and applied for BG level prediction (Supplementary Table 1).
The Effect of Missing Data Imputation on BG Level Prediction
We measured the accuracy of each imputation method on BG level prediction. We trained XGBoost models using training sets, which were imputed with different imputation methods (see Methods for details). To examine different aspects of prediction accuracy, we used three evaluation metrics: RMSE, MAE, and PCC. Overall, the models achieved RMSE of 16.13 ± 2.77 in a training set (MAE = 11.48 ± 1.98 and PCC = 0.96 ± 0.01; Fig. 3a and Supplementary Table 5). The lowest RMSEs were achieved with linear interpolation (LI, RMSE = 12.55 ± 3.18), Stineman interpolation (STI, RMSE = 13.23 ± 2.78), and Kalman smoothing with structural model (KS, RMSE = 13.16 ± 3.53). As expected, random imputation methods showed the largest RMSEs (random, RMSE = 21.09 ± 7.38; and Emp-random, RMSE = 21.80 ± 5.91; Supplementary Table 5).
Fig. 3.
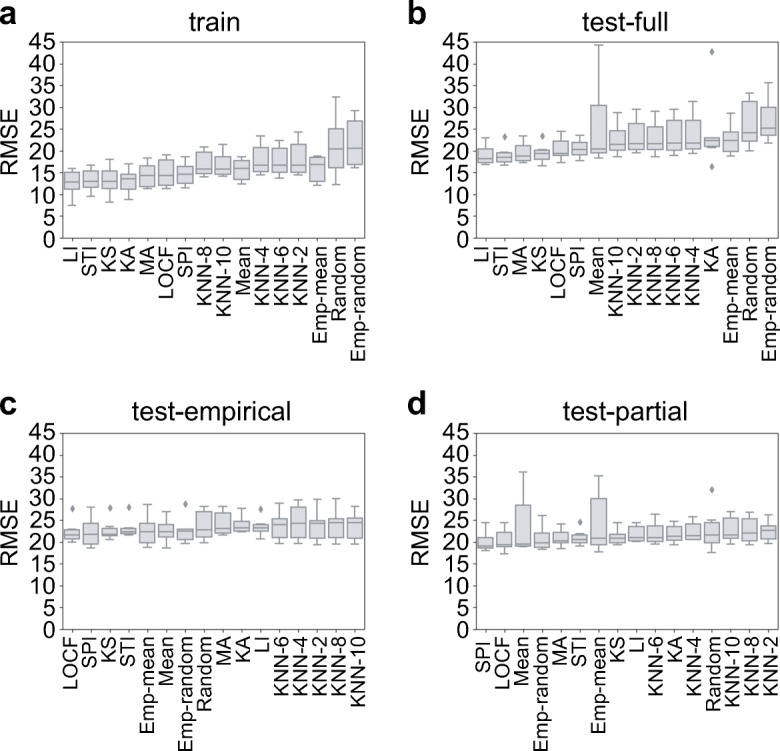
The performance of predictive models. Predictive models were trained using training sets that were imputed by 16 imputation methods. The models were applied to a training set, b test-full set, c test-empirical set, and d test-partial set. RMSE was used to measure the prediction accuracy
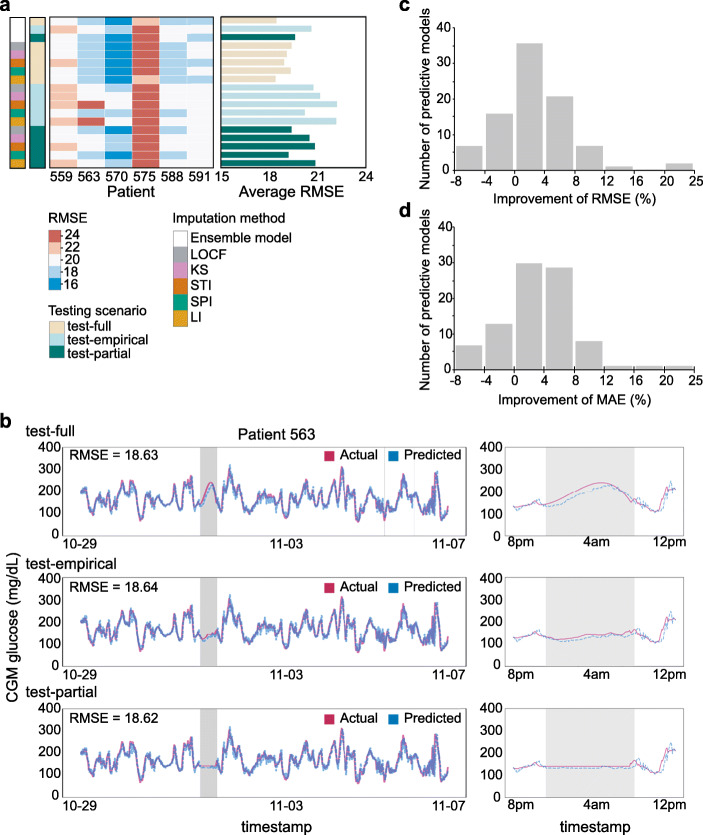
To evaluate the performance of our predictive models in a test set, we compared three possible testing scenarios, conventional train-test setting (test-full) and two realistic deployment settings (test-empirical and test-partial). We observed that spline interpolation (SPI) and Kalman smoothing with structural model (KS) generally showed lower RMSE than other methods across all testing scenarios (Fig. 3b–d). Note that in Fig. 3b, linear interpolation-based imputation methods perform best (RMSE = 19.07 ± 2.02; MAE = 13.47 ± 1.28; and PCC = 0.94 ± 0.02); however, they are not compatible with realistic deployment, as interpolation-based methods would need a point from the future to impute data gaps in the present. Interestingly, a model imputed with LOCF also showed relative high prediction accuracy in test-empirical and test-partial suggesting that carrying forward the last observed value led to better BG level prediction. Potentially, consideration of more values from the past could help further improve prediction in the presence of missing data.
To identify generally effective imputation methods for BG level prediction, we first grouped imputation methods based on their RMSEs, MAEs, and PCCs on training sets, which were imputed by 16 different imputation methods (Fig. 4a). We identified one cluster that showed high prediction accuracies regardless of evaluation metrics (i.e. the cluster was enriched with low RMSEs, low MAEs, and high PCCs; red dashed box in Fig. 4a). Next, we examined variances of prediction accuracies across entire patients in training sets. Small variance indicated that a given imputation method achieved high prediction accuracies in all patients. Finally, we selected the top five imputation methods (STI, SPI, LOCF, KS, and LI) based on rank products, which were consensus rankings across the observed rankings of RMSE variances, MAE variances, and PCC variances (Fig. 4b). We considered these five methods as generally effective imputation methods and used them for further analyses.
Fig. 4.
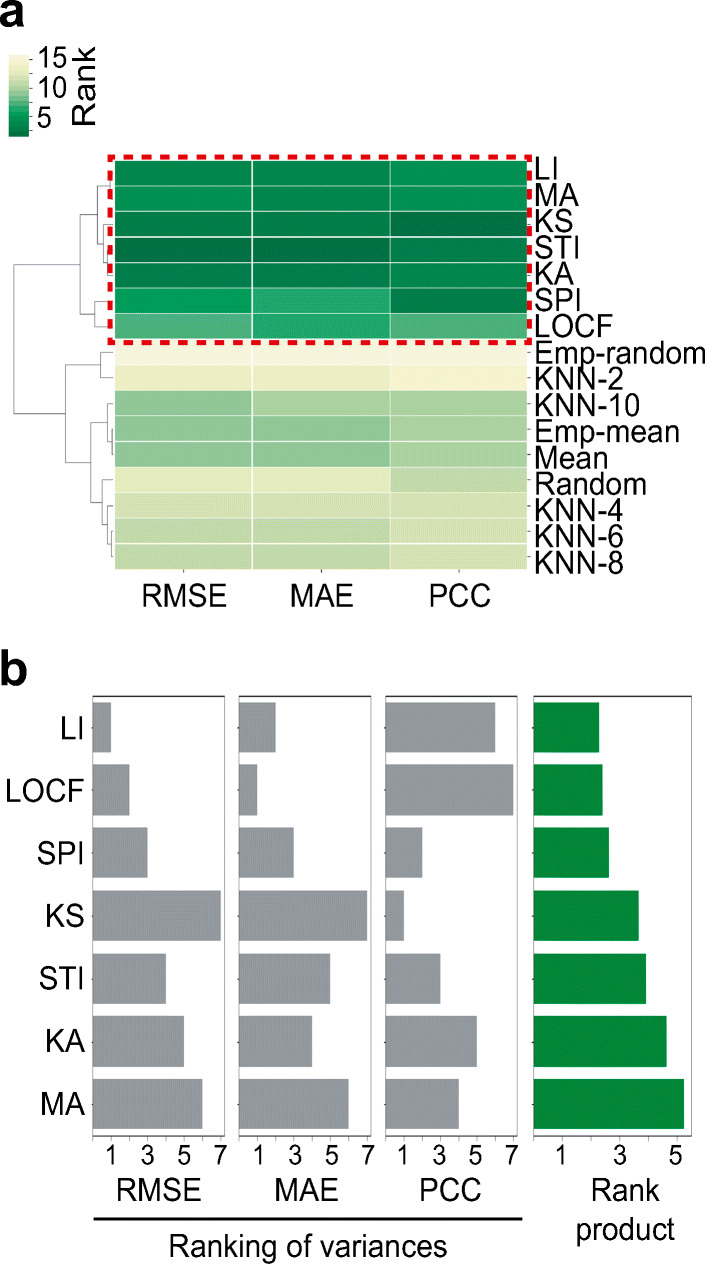
The selection of optimal set of imputation methods. a Cluster map between 16 imputation methods and 3 evaluation metrics. Hierarchical clustering with Euclidean distance matrix and complete linkage method was performed. Red-dashed box indicated a group of imputation methods that showed relatively high overall accuracies (low RMSE, low MAE, and high PCC). b Rankings of imputation methods based on variances of RMSEs, MAEs, and PCCs across patients (grey bars). Rank product which was an aggregate rank across observed rankings of RMSE variances, MAE variances, and PCC variances was shown (green bars)
Building a Predictive Model for Blood Glucose Levels
Based on the observation that physiological measurements, monitoring signals, and lagged-time features all play a part in determining BG levels in T1D patients, we built five predictive models using XGBoost that used training data imputed by the top five imputation methods. All 320 features were used to build XGBoost models with hyperparameter optimization in the training set. From the hyperparameter optimization, we observed that the average percent difference in RMSE between the best and worst parameter combination was 9% (minimum 4% and maximum 22%; Supplementary Fig. 3).
We found that five predictive models showed competitive performance in any given testing scenario (Fig. 5a). Predictive models showed overall RMSE of 19.02 ± 2.52 in a test-full (conventional setting, MAE = 13.39 ± 1.46 and PCC = 0.94 ± 0.02), 21.29 ± 2.54 in a test-empirical (realistic setting, MAE = 14.96 ± 1.32 and PCC = 0.93 ± 0.02), and 20.15 ± 2.20 in a test-partial (realistic setting, MAE = 14.41 ± 1.31 and PCC = 0.93 ± 0.02; Table 2 and Supplementary Table 6). Moreover, patients showed similar prediction performance across different test scenarios (Fig. 5b and Supplementary Fig. 4). For example, predictive models for Patient 563, which were imputed by spline interpolation, yielded RMSE of 18.63 (MAE = 13.11 and PCC = 0.92) in the test-full scenario. The real-time BG level predictions showed similar RMSE of 18.64 (MAE = 13.09 and PCC = 0.92) in test-empirical and RMSE of 18.62 (MAE = 13.04 and PCC = 0.92) in test-partial (left panel in Fig. 5b). Interestingly, we found that, in the test-empirical setting (test set was imputed by Emp-mean), the predictive model produced the most probable BG levels (right-middle panel in Fig. 5b) by using as much information as possible from previously observed values. Meanwhile, in the test-full setting (test set was imputed by SPI), the spline interpolation smoothly connected the start point to the end point of missing value period which could be artificially inflated (right-top panel in Fig. 5b). In the test-partial setting (test set was imputed by LOCF), the predictive model produced unrealistically constant BG levels, which could lead prediction failure when signal was lost before a drop in BG levels (right-bottom panel in Fig. 5b).
Fig. 5.
Performance of predictive models. a RMSE of each patient was measured in different testing scenarios; test-full, test-empirical, and test-partial. Blue and red represented small and large RMSE, respectively. b Comparison between actual observed (red) and predictive (blue) BG levels. Timestamps which had missing glucose levels were coloured as grey. Comparisons through entire tested timeframe (left) and ± 4 hours from missing timestamps (right) were presented. Observed and predictive glucose levels of Patient 563 in different testing scenarios were compared. Training set was imputed by spline interpolation. c and d Performance improvement of ensemble models over individual models. Percentage of RMSE (c) and MAE (d) improvement was measured from the comparison between the performances of ensemble models and those of five individual predictive models
Table 2.
Prediction accuracy of 30-minute BG level for the top five imputation methods and ensemble models
| Imputation method | Test-full | Test-empirical | Test-partial |
|---|---|---|---|
| Last observed carried forward (LOCF) | 19.38 ± 2.53 | 20.74 ± 2.63 | 19.38 ± 2.53 |
| Kalman smoothing with structural model (KS) | 19.09 ± 3.11 | 21.16 ± 2.63 | 20.49 ± 2.20 |
| Stineman interpolation (STI) | 18.92 ± 2.69 | 22.20 ± 2.37 | 20.83 ± 1.90 |
| Spline interpolation (SPI) | 19.32 ± 2.55 | 20.20 ± 2.92 | 19.20 ± 2.59 |
| Linear interpolation (LI) | 18.39 ± 2.51 | 22.16 ± 2.38 | 20.86 ± 1.82 |
| Overall performance of individual models | 19.02 ± 2.52 | 21.29 ± 2.54 | 20.15 ± 2.20 |
| Ensemble model | 18.45 ± 2.55 | 20.61 ± 2.55 | 19.59 ± 2.20 |
*average RMSE ± standard deviation of RMSEs were tabulated
It has been well known that combining multiple prediction models can yield more accurate and generalizable forecasts. We therefore decided to build an ensemble model by integrating the five previously generated predictors for the generalized prediction of BG level at each timestamp. The ensemble model outperformed individual predictive models (Fig. 5a). The ensemble model achieved RMSE of 18.45 ± 2.55 (MAE = 12.94 ± 1.42 and PCC = 0.94 ± 0.02, test-full), 20.61 ± 2.55 (MAE = 14.49 ± 1.14 and PCC = 0.93 ± 0.02, test-empirical), and 19.59 ± 2.20 (MAE = 13.99 ± 1.11 and PCC = 0.94 ± 0.02, test-partial; Table 2 and Supplementary Table 6). Overall, the ensemble model improved RMSE and MAE up to 22% compared to five individual predictors in all three test settings (Fig. 5c and d). Ensemble model delivered prediction improvement of 4–8% compared to more than half of individual predictors when we measured RMSE and MAE as evaluation metrics. PCC showed relatively less improvement (Supplementary Fig. 5) since individual predictors already achieved strong correlation (Pearson’s r > 0.9) between observed and predicted BG levels in test sets. Ensemble models showed competitive performance in both realistic deployment settings (test-empirical and test-partial) and conventional setting (test-full; box plots in Fig. 5c and d). These results indicated that the ensemble models could provide reliable BG levels in real-time prediction settings.
Characterization of Relevance of Features to Predict Blood Glucose Level
Given the diversity of features originated from physiological measurements and monitoring signals, we examined their importance to predict BG levels. We measured the feature importance of all 320 features using the Random Forest algorithm and prioritized them using recursive feature elimination (RFE) [34]. Feature importance implied the ability of individual features to predict BG levels. We found that in all patients, features derived from quasi-continuous features were more likely to be important for BG level prediction compared to one-off features (Fig. 6a). Overall, BG level-related features such as time-lagged glucose levels, difference of glucose levels between timestamps, and finger-stick glucose level were ranked within the top 50 important features in all patients. Meanwhile, one of one-off features, area under the graph of insulin bolus dose (bolus square), showed patient-specific importance. In Patient 570, insulin bolus dose was more important in predicting BG levels compared to in other patients (Supplementary Fig. 6). Other one-off features such as exercise intensity and work intensity showed relatively less importance to predict BG levels in all patients.
Fig. 6.
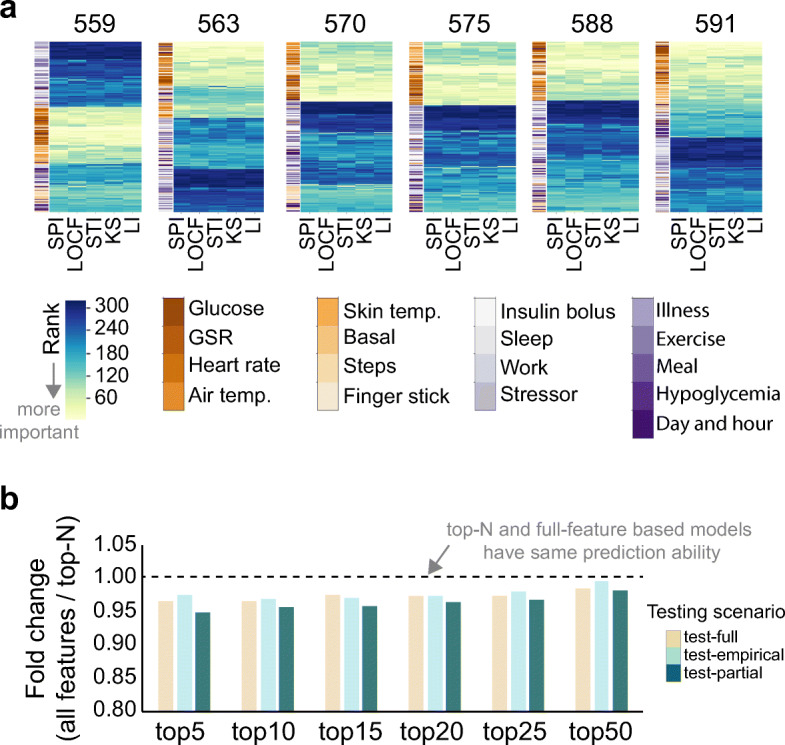
Feature importance to predict BG levels. a Feature importance was measured using Random Forest regression algorithm and prioritized (rank). Features (Y-axis) was clustered based on rank similarities across imputation methods. Yellow indicated top-ranked features, and blue indicated bottom-ranked features. Feature importance was measured in training sets which were imputed by different imputation methods. GSR indicated galvanic skin response. b Relative performance of predictive models that were generated by top-N features (N = 5 ~ 50). Fold change represented relative performance of top-N-based models compared to all-feature-based model.
To examine whether only a set of relevant features were enough to predict BG levels, we sequentially selected the top 5 to 50 most important features, trained models on each subset, and compared RMSEs with that of the all-feature model. We found that although the all-feature-based model still achieved the best performance, top-N-feature-based predictive models had competitive prediction abilities, and model performance approached the original model with increasing N (Fig. 6b). On average, the top-5 feature model showed a 4% difference from the all-feature based model (0.96-fold change). Top-25- and top-50-feature models achieved RMSEs 3% (0.97-fold change) and 1% (0.99-fold change) worse than the all-feature based model, respectively. Interestingly, using Emp-mean values for test set imputation performed slightly better than LOCF imputation when using top-5 to top-50 features to build XGBoost BG level predictors. These findings suggest that about 15% (50 out of 320 features) of relevant features could be sufficient to capture key information to predict BG levels.
Discussion
While currently available imputation methods can be readily applied to training data, imputation on test sets is unconventional due to the temporal nature of time series features. Thus, imputing test sets requires careful consideration of applicability in realistic online prediction settings. In a realistic setting of BG level prediction (e.g. online monitoring and prediction), unexpected events, such as loss of signal, sensor malfunction, power loss of monitoring devices, and human error, may throw predictions off-targets. These missing values potentially cause inaccurate prediction of BG levels and restrict to identify hypo- and hyperglycaemia. Therefore, appropriate missing value imputation would be essential for the successful management of data and accurate model generation based on machine-learning and deep-learning algorithms. It has been shown that missing values and imputation methods can affect the training of a neural network when using backpropagation [35]. It would be possible that multiplying missing values with a weight and adding a bias during backpropagation would make a poor predictive model. Other studies which used deep-learning algorithms have noted the inability of artificial neural networks to handle incomplete data for the prediction [36] and imputed missing values using interpolation and extrapolation-based imputation methods [4, 6]. Also, adding a missing value indicator (e.g. 1 = observed value and 0 = missing value that was imputed) improved prediction of patient mortality and their diagnostic category [16]. Although machine-learning and deep-learning-based approaches have been broadly applied to various predictive models, the effect of imputation on prediction performance has not yet been fully explored.
In this study, we investigated the importance of physiological and monitoring features to predict BG level and expanded on our work in discerning which imputation methods could have potential benefits in both the training and the testing/deployment phases. We also developed a novel imputation method for time series dataset, Emp, and found that this method can impute the most probable BG levels at a given timestamp. Furthermore, we investigated the effect of various imputation methods on BG level prediction and identified an optimal set of imputation methods that can improve the prediction accuracy. Finally, we demonstrated that ensemble models improved prediction accuracy over individual predictive models (Supplementary Table 2) and models from our previous approach (Supplementary Table 7): ensemble model improved prediction accuracy by about 5% and 1% in both conventional and realistic settings (for the fair comparison, prediction performances on untrimmed test sets were compared). Furthermore, accuracies of the ensemble model on untrimmed test sets were 2% to 16% higher than those of other deep-learning-based works also trained on the OhioT1DM datasets [1, 4, 6, 7]. We suspected that the lack of interpretability of deep-learning models would limit to explain why the model predicted a particular glucose value. Meanwhile, decision tree-based model (e.g. XGBoost) enabled us to determine the plausible precisions made by the model in order to generate a predictive value.
For the ensemble modelling, we selected top five predicted models that were imputed by linear interpolation (LI), last observed carried forward (LOCF), spline interpolation (SPI), Kalman smoothing with structural models (KS), and Stineman interpolation (STI). We further examined the prediction accuracy of ensemble models by selecting top seven to two imputation methods (reducing the number of imputation methods based on rank product). We observed that, regardless of the number of selected imputation methods, ensemble models generally showed higher prediction accuracy compared to a single predictive model. Meanwhile, the number of imputation methods that showed the highest accuracy was different depending on testing scenarios and patients (Supplementary Table 8). Taken together, ensemble modelling could improve both accuracy and generalizability of blood glucose level prediction, and these benefits were realized from analysis of only six patients. Use of additional patients, who have different level of missing values, may refine the assessment of imputation methods and ensemble model and increase the accuracy of blood glucose level prediction.
Across different patients, we found variations in which time-lagged features within the past hour most strongly impacted the current glucose level. We reasoned that different lifestyle behaviours, living environments, and genetic background would affect these varying associations between BG level and time-lagged features. It has been shown that long-term dietary treatment with fibre-rich foods improved blood glucose control through the fast reduction of blood glucose after meal intake, and the restoring time of BG level to its normal range differed depending on meal type (e.g. breakfast, lunch, and dinner) in T1D patients [37]. Also, more than 20 genetic loci have been identified to contribute to T1D susceptibility [38], showing that T1D is a heterogeneous and polygenic disorder. Taken together, we believe that time-lagged versions of features could be key factors for building personalized predictors of BG levels.
The last decade has seen tremendous advances in elucidating genetic factors and epidemiology and developing clinical interventions in type 1 diabetes. The improvement of treatment options to control BG level such as continuous glucose monitoring and insulin pump therapy has helped clinicians and patients to manage the disease and control insulin administration. Despite these efforts, there remains an urgent need for accurate prediction of blood glucose level for T1D patients in both conventional and especially realistic settings. Examined features in our study which were derived from health monitoring and wearable devices can act as partial surrogates for genetic and physiological testing, and incorporating these features into common clinical practice could improve the risk assessment, treatment, and control of type 1 diabetes.
Conclusion
This study described a machine-learning approach using XGBoost to predict blood glucose levels on a 30-minute horizon. We explored the effectiveness of missing data imputation methods in both training and test settings. Our experiments demonstrated that the top five imputation methods for BG level prediction were carrying forward the last observed value, linear interpolation, spline interpolation, Stineman interpolation, and Kalman smoothing with structural models. Predictive models were benchmarked in three testing scenarios; one train-test conventional setting and two realistic deployment settings.
While individual models using different imputation methods performed well, ensemble models that aggregated predictions from all five models showed ~ 10% improvement in RMSE in realistic settings over any model alone. We investigated feature importance across current and past feature values and demonstrated that time-lagged features are important features for building personalized BG level predictors. Finally, we trained top-N-feature-based predictive models, showing that significantly smaller feature sets yielded competitive prediction abilities and providing promising results for future deployment of lightweight BG prediction models.
Electronic supplementary material
(DOCX 5470 kb)
Acknowledgements
We would like to thank all members of the Labs team at Klick Inc. for their helpful advice and assistance. We would also like to thank Cooper Midroni and Maheedhar Kolla for technical support.
Compliance with Ethical Standards
Conflict of Interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Footnotes
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Jouhyun Jeon, Email: [email protected].
Alfred J. Whitehead, Email: [email protected]
References
- 1.Bertachi A, Biagi L, Contreras I, et al. Prediction of blood glucose levels and nocturnal hypoglycemia using physiological models and artificial neural networks. CEUR Workshop Proc. 2018;2148:85–90. [Google Scholar]
- 2.Atkinson MA (2012) The pathogenesis and natural history of type 1 diabetes. 1–18. 10.1101/cshperspect.a007641
- 3.Wild D, von Maltzahn R, Brohan E, Christensen T, Clauson P, Gonder-Frederick L. A critical review of the literature on fear of hypoglycemia in diabetes: implications for diabetes management and patient education. Patient Educ Couns. 2007;68:10–15. doi: 10.1016/j.pec.2007.05.003. [DOI] [PubMed] [Google Scholar]
- 4.Zhu T, Li K, Herrero P, et al. A deep learning algorithm for personalized blood glucose prediction. CEUR Workshop Proc. 2018;2148:74–78. [Google Scholar]
- 5.Martinsson J, Schliep A, Eliasson B, et al. Automatic blood glucose prediction with confidence using recurrent neural networks. CEUR Workshop Proc. 2018;2148:64–68. [Google Scholar]
- 6.Chen J, Li K, Herrero P, et al. Dilated recurrent neural network for short-time prediction of glucose concentration. CEUR Workshop Proc. 2018;2148:69–73. doi: 10.1177/0363546510373570. [DOI] [Google Scholar]
- 7.Contreras I, Bertachi A, Biagi L, et al. Using grammatical evolution to generate short-term blood glucose prediction models. CEUR Workshop Proc. 2018;2148:91–96. [Google Scholar]
- 8.Pappada SM, Cameron BD, Rosman PM. Development of a neural network for prediction of glucose concentration in type 1 diabetes patients. J Diabetes Sci Technol. 2008;2:792–801. doi: 10.1177/193229680800200507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sudharsan B, Peeples M, Shomali M. Hypoglycemia prediction using machine learning models for patients with type 2 diabetes. J Diabetes Sci Technol. 2015;9:86–90. doi: 10.1177/1932296814554260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Frandes M, Timar B, Timar R, Lungeanu D. Chaotic time series prediction for glucose dynamics in type 1 diabetes mellitus using regime-switching models. Sci Rep. 2017;7:6232. doi: 10.1038/s41598-017-06478-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rodbard D. Continuous glucose monitoring: a review of successes, challenges, and opportunities. Diabetes Technol Ther. 2016;18:S2-3–S2-13. doi: 10.1089/dia.2015.0417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Midroni C, Leimbigler PJ, Baruah G, et al. Predicting glycemia in type 1 diabetes patients: experiments with XGBoost. CEUR Workshop Proc. 2018;2148:79–84. [Google Scholar]
- 13.Bach K, Bunescu RC, Farri O, et al (2018) Proceedings of the 3rd International Workshop on Knowledge Discovery in Healthcare Data co-located with the 27th International Joint Conference on Artificial Intelligence and the 23rd European Conference on Artificial Intelligence (IJCAI-ECAI 2018). CEUR-WS.org
- 14.Marling C, Bunescu R. The OhioT1DM dataset for blood glucose level prediction. CEUR Workshop Proc. 2018;2148:60–63. [PMC free article] [PubMed] [Google Scholar]
- 15.Marling C, Bunescu RC (2018) The OhioT1DM dataset for blood glucose level prediction. In: Proceedings of the 3rd International Workshop on Knowledge Discovery in Healthcare Data co-located with the 27th International Joint Conference on Artificial Intelligence and the 23rd European Conference on Artificial Intelligence {(IJCAI-ECAI} 2018), Sto. pp 60–63
- 16.Che Z, Purushotham S, Cho K, et al. Recurrent neural networks for multivariate time series with missing values. Sci Rep. 2018;8:6085. doi: 10.1038/s41598-018-24271-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Johnson SA, Stedinger JR, Shoemaker CA, et al. Numerical solution of continuous-state dynamic programs using linear and spline interpolation. Oper Res. 1993;41:484–500. doi: 10.1287/opre.41.3.484. [DOI] [Google Scholar]
- 18.Jalles JT (2009) Structural time series models and the Kalman filter: a concise review. SSRN Electron J. 10.2139/ssrn.1496864
- 19.Moritz S, Bartz-Beielstein T. imputeTS: time series missing value imputation in R. The R Journal. 2017;9:207–218. doi: 10.32614/RJ-2017-009. [DOI] [Google Scholar]
- 20.Stineman RW. A consistently well behaved method of interpolation. Creat Comput. 1980;6:54–57. [Google Scholar]
- 21.Johannesson T, Bjornsson H, Grothendieck G (2009) Package “stinepack.” In: Icelandic Meterological Off.
- 22.Zeileis A, Grothendieck G. zoo: S3 Infrastructure for regular and irregular time series. J Stat Softw. 2005;14:1–27. doi: 10.18637/jss.v014.i06. [DOI] [Google Scholar]
- 23.faucyimpute 0.5.2. https://github.com/iskandr/fancyimpute
- 24.Zhang S. Parimputation: from imputation and null-imputation to partially imputation. IEEE Intell Inform Bull. 2008;9:32–38. [Google Scholar]
- 25.Chen T, Guestrin C (2016) Xgboost: a scalable tree boosting system. In: Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining. pp 785–794
- 26.Torlay L, Perrone-Bertolotti M, Thomas E, Baciu M. Machine learning-XGBoost analysis of language networks to classify patients with epilepsy. Brain Inform. 2017;4:159–169. doi: 10.1007/s40708-017-0065-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chambon S, Galtier M, Arnal P, et al (2017) A deep learning architecture for temporal sleep stage classification using multivariate and multimodal time series [DOI] [PubMed]
- 28.Bergmeir C, Benítez JM. On the use of cross-validation for time series predictor evaluation. Info Sci. 2012;191:192–213. doi: 10.1016/j.ins.2011.12.028. [DOI] [Google Scholar]
- 29.Jones E, Oliphant T, Peterson P, others SciPy: Open source scientific tools for Python
- 30.Pedregosa F, Varoquaux G, Gramfort A, et al. Scikit-learn: machine learning in Python. J Mach Learn Res. 2011;12:2825–2830. [Google Scholar]
- 31.Waskom M, Botvinnik O, O’Kane D, et al (2018) mwaskom/seaborn: v0.9.0 (July 2018)
- 32.DeSalvo D, Buckingham B. Continuous glucose monitoring: current use and future directions. Curr Diab Rep. 2013;13:657–662. doi: 10.1007/s11892-013-0398-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Breiman L. Random forests. Mach Learn. 2001;45:5–32. doi: 10.1023/A:1010933404324. [DOI] [Google Scholar]
- 34.Guyon I, Weston J, Barnhill S, Vapnik V. Gene selection for cancer classification using support vector machines. Mach Learn. 2002;46:389–422. doi: 10.1023/A:1012487302797. [DOI] [Google Scholar]
- 35.Vamplew P, Adams A (1992) Missing values in a backpropogation Neural Net. Proc third Aust Conf neural networks, Sidney 64–67
- 36.Ennett CM, Frize M, Walker CR. Influence of missing values on artificial neural network performance. Stud Health Technol Inform. 2001;84:449–453. [PubMed] [Google Scholar]
- 37.Giacco R, Parillo M, Rivellese AA, et al. Long-term dietary treatment with increased amounts of fiber-rich low-glycemic index natural foods improves blood glucose control and reduces the number of hypoglycemic events in type 1 diabetic patients. Diabetes Care. 2000;23:1461–1466. doi: 10.2337/diacare.23.10.1461. [DOI] [PubMed] [Google Scholar]
- 38.Atkinson MA, Eisenbarth GS. Type 1 diabetes: new perspectives on disease pathogenesis and treatment. Lancet. 2001;358:221–229. doi: 10.1016/S0140-6736(01)05415-0. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(DOCX 5470 kb)