Abstract
Breast cancer is the most common cancer diagnosed in women worldwide. Up to 50% of non-palpable breast cancers are detected solely through microcalcification clusters in mammograms. This article presents a novel and completely automated algorithm for the detection of microcalcification clusters in a mammogram. A multiscale 2D non-linear energy operator is proposed for enhancing the contrast between the microcalcifications and the background. Several texture, shape, intensity, and histogram of oriented gradients (HOG)–based features are used to distinguish microcalcifications from other brighter mammogram regions. A new majority class data reduction technique based on data distribution is proposed to counter data imbalance problem. The algorithm is able to achieve 100% sensitivity with 2.59, 1.78, and 0.68 average false positives per image on Digital Database for Screening Mammography (scanned film), INbreast (direct radiography) database, and PGIMER-IITKGP mammogram (direct radiography) database, respectively. Thus, it might be used as a second reader as well as a screening tool to reduce the burden on radiologists.
Electronic supplementary material
The online version of this article (10.1007/s10278-019-00249-5) contains supplementary material, which is available to authorized users.
Keywords: 2D NEO, Non-linear energy operator, NEO, Microcalcification, Microcalcification clusters, Mammogram, Shape features, Texture features, SVM classifier
Introduction
Breast cancer is the second most frequently diagnosed cancer in the world with 2.1 million new cases in 2018. It is the most common cancer diagnosed in women and accounts for approximately 25% of all cancer cases in women worldwide. Breast cancer is the fifth most common cause of death leading to 626,679 cancer deaths worldwide in 2018 [1]. In India, an estimated 145,000 cases were diagnosed with breast cancer, and about 70,000 breast cancer patients died in 2012 [12]. The detection of breast cancer at an early stage can help to reduce the suffering of the patients, mortality rate, and expense of treatment.
Mammography is the most efficient and well-known technique for the early detection of breast cancer. There are various abnormalities found in mammograms, including microcalcification, mass, architectural distortion, and bilateral asymmetry, which can act as early signs of breast cancer. Microcalcifications are tiny specks of mineral deposits such as calcium. They are found scattered throughout the breast tissue, and they often occur in clusters. Microcalcification (MC) clusters solely act as an early indicator of up to 50% of all non-palpable breast cancers. They are also present in about 93% of cases of ductal carcinoma in situ (DCIS). Thus, detection of MC clusters is very crucial in the diagnosis of breast cancer [6]. Computer-aided diagnosis (CAD) system can act as a second reader and can help the radiologists to find MC clusters that radiologist otherwise might have missed.
Due to the increase in the number of cancer cases every year, the workload of radiologists is increasing. The ratio of radiologists to population is 1:50,000 in the USA and Europe, while many African countries have a ratio of 1:1,000,000 or worse. Fourteen African countries have no radiologists, and most have fewer than 30 [2]. So, there is a massive burden on radiologists for diagnosing such a large population. There is a need for screening CAD which can predict the normal cases with 100% confidence so that radiologist does not have to check most of the normal cases and thereby reducing their workload. Thus, we aim for developing an automated algorithm which can detect microcalcification clusters with 100% sensitivity at low false positives per image.
Related Works on the Detection of Microcalcifications
Several preprocessing techniques are proposed for pre-emphasizing the microcalcifications. Conventional enhancement techniques include contrast stretching, histogram equalization, and enhancement using convolution mask. As the conventional methods are often based on global transformation which is not so effective, many approaches were proposed to enhance the mammogram images using local enhancement techniques [4, 32]. Gurcan et al. [16] processed the mammogram images by a subband decomposition filterbank and used higher order statistical parameters such as skewness, kurtosis, etc. to detect microcalcification clusters. Papadopoulos et al. [29] have compared various preprocessing techniques like linear range modification (LRM), contrast-limited adaptive histogram equalization (CLAHE), and wavelet-based preprocessing and shown that the best results are obtained using LRM-based preprocessing. Morphological processing [9, 27] and wavelet reconstruction [42] are also some of the successful methods which enhance microcalcifications and suppress other high-intensity regions in mammograms.
Many techniques are focused on feature extraction and selection. Kim and Park [21] have compared the performance of different features from spatial gray-level dependence method (SGLDM), gray-level run-length method (GLRLM), gray-level difference method (GLDM), and the surrounding region-dependence method (SRDM) for microcalcification detection and shown that SRDM outperforms other features. Zadeh et al. [37] compared the performance of four different types of features, namely shape-, texture-, wavelet-, and multi-wavelet-based features and concluded that multi-wavelet performs relatively better compared with other features.
Extensive research has been performed on the detection and classification of microcalcifications using machine learning techniques. Yu and Guan [43] proposed a completely automated two-stage neural network approach in which wavelet features, gray-level statistics, and shape features were used to train two neural networks. It achieved a sensitivity of 90% with 0.5 false positives (FPs) per image. El-Naqa et al. [11] used support vector machines (SVM) to detect microcalcification clusters and achieved a sensitivity of 94% at one FP per image. Wei et al. [39] proposed a Bayesian learning approach known as Relevance Vector Machines (RVM). The method is computationally efficient and provides similar performance when compared with SVM with 90% sensitivity at one FP per image. Nakayama et al. [26] proposed a Hessian matrix–based filter bank for extracting multiscale features. Peng et al. [30] proposed an algorithm based on stochastic resonance noise for detecting microcalcifications. Guo et al. [15] proposed a MC cluster detection algorithm which uses contourlet transform and pulse-coupled neural network (PCNN). Liu et al. [23] used the possibilistic fuzzy c-means (PFCM) clustering and weighted support vector machine (WSVM) and reported the sensitivity of 92% with 2.3 FP per image. Shin et al. [36] used discriminative restricted Boltzmann machine (DRBM) and reported Az value of 0.8294. Zhang et al. [44] proposed morphological image processing and wavelet transform–based method to microcalcification clusters. The said method reported the sensitivity of 92.9% with 0.08 false positive per image. Chen et al. [3] proposed a method for classification of microcalcification clusters using the topology of individual microcalcifications and reported accuracy up to 96% and Az value up to 0.96. Rampun et al. [31] analyzed the performance of 11 classifiers for classification of microcalcification clusters using confidence levels for each classifier. The study shows the importance of investigating confidence levels in the development of CAD systems. Mordang et al. [24] proposed a semi-automated deep learning–based technique for the detection of microcalcification clusters in which the regions of interest or patches of size 13×13 pixels are manually cropped and are classified as microcalcification clusters or normal regions. The method achieved the sensitivity close to 100% at high false positive per image (more details are given in Section 1 of the Supplementary Material). The method by Mordang et al. have not reported the results in terms of number of true positive and false positive microcalcification clusters. There is no paper on automated detection of microcalcification cluster detection using deep learning to the best of our knowledge. Note that the performance of microcalcification detection algorithms is highly dependent on the database and the criteria on which the results are evaluated. Karale et al. [20] proposed a modified unsharp masking for the enhancement of microcalcifications. The sensitivity of 96.72% with 3.48 FP per image and 96.05% with 1.81 FP per image are reported on Digital Database for Screening Mammography (DDSM) and private database, respectively. In this work, two novel multiscale 2D NEO operators are proposed which can detect even subtle microcalcifications of various sizes and shapes. In addition to this, a new majority class data reduction technique based on data distribution is proposed to counter data imbalance problem in a more efficient way.
Database
The performance of the proposed method is evaluated on three different databases, namely Digital Database for Screening Mammography (DDSM) [33] and INbreast database which are publicly available and third is PGIMER-IITKGP mammogram database which is collected by doctors of PGIMER for the researchers of IITKGP. The DDSM contains scanned film images digitized at the resolution of 0.05 mm, 0.042 mm, and 0.0435 mm with 16-bit grayscale resolution. DDSM is the largest, popular, and freely available database. From DDSM, 100 normal images and 97 images with 100 microcalcification clusters (one or two microcalcification clusters per mammogram) are selected for this study. DDSM provides mammographer-assigned subtlety ratings on the scale of 1 to 5, where 1 indicates most subtle, and 5 indicates the obvious cases. Twenty microcalcification clusters are selected from each subtlety level for an unbiased evaluation of proposed algorithms.
PGIMER-IITKGP mammogram database is direct radiography (DR)-type private database having a resolution of 0.07 mm and a grayscale resolution of 12 bits, acquired from Post Graduate Institute of Medical Education and Research, Chandigarh, India. A set of 110 images, including 50 normal images and 60 images having one to five microcalcification clusters, are selected. The subtlety rating information of microcalcification clusters is not available for the PGIMER-IITKGP mammogram database.
The publicly available DR-type INbreast database has a resolution of 0.07 mm and a grayscale resolution of 14 bits. The database contains 410 images, including 389 images without microcalcification clusters and 21 images having one to three microcalcification clusters. The subtlety ratings of microcalcification clusters are not provided by the INbreast database. The locations of individual microcalcifications in the clusters for PGIMER-IITKGP database are identified by the experienced radiologist TS. In the case of DDSM and INbreast databases, the cluster boundaries are provided by the DDSM and INbreast database. The microcalcifications in the clusters are marked by the experienced radiologist, AS, for DDSM and INbreast database. INbreast database reports 27 microcalcification clusters in 21 images. As one cluster is found with less than three microcalcifications, radiologist AS has merged it with the adjacent cluster. Hence, we have 21 images with 26 microcalcification clusters in INbreast database in our study.
The details about the databases used are given in Table 1.
Table 1.
Database details
| Database | Total no. of images | No. of images without MC clusters | No. of images with MC | No. of MC clusters |
|---|---|---|---|---|
| DDSM | 197 | 100 | 97 | 100 |
| INbreast | 410 | 389 | 21 | 26 |
| PGIMER | 110 | 50 | 60 | 76 |
Proposed Method for the Detection of MC Clusters
The block diagram of the proposed algorithm is shown in Fig. 1. It consists of the following steps.
Fig. 1.
Block diagram of the proposed microcalcification detection method
Preprocessing
Breast Region Segmentation
First, breast region is segmented using multilevel hierarchical thresholding (MLHT) [14, 34] to limit the search within the breast region. It also helps to remove various artifacts like tags or labels outside the breast region which may be detected as microcalcifications due to their high-intensity.
Pre-emphasis
Microcalcifications appear as tiny bright spots in mammograms. Since they often have very low contrast with respect to the background, a novel multiscale 2D non-linear energy operator (2D NEO) is proposed, which can enhance the contrast of microcalcifications over the background in mammograms. The Teagers energy operator (TEO) [18] is a non-linear energy operator in 1D and defined as:
where “x” is the input signal in 1D and x(n) is the value at nth sample number. Initially, TEO was used to measure the instantaneous energy of a signal [18]. Later, Mukhopadhyay and Ray [25] have given the statistical interpretation of TEO and have shown that it can be effectively used to detect spikes in 1D signals. In a similar way, 1D NEO can be extended in 2D for the detection of peaks in mammogram images. For the extension of the 1D NEO operator to 2D NEO operator, two possibilities are experimented, and the best one is selected. In the first case, 1D NEO operator is applied on the pair of pixels from 4 neighborhood of the central pixel in x direction and y direction only. The filter response in x direction and y direction is added to get a final response at that pixel location. In the second case, the 2D NEO response is calculated by combining the responses of 1D NEO operator applied on each pair of pixels from 8 neighborhood of central pixel, unlike the first case. According to Mukhopadhyay and Ray, NEO operator should be followed by moving average filter to remove spurious spikes. Accordingly, the response of 2D NEO operator is convolved twice with the 3×3 box filter [13] in both cases. The rotation invariance property of these two approaches is compared to select the best representative method. For this, an ROI of 61×61 pixels centered at a microcalcification object is cropped. The ROI is rotated at various angles and the 2D NEO is applied on cropped ROI and its rotated version.
Figure 2 shows the 2D NEO responses of an ROI and the rotated ROI by 45∘ for both the cases with the center of ROI marked by “+” in red color. Although it is expected that the 2D NEO response of rotated and normal ROIs are equal, a small difference is observed between them. In order to demonstrate this, the absolute error at the center pixel vs. angle of rotation is plotted which is shown in Fig. 3. As shown, the difference in absolute errors is highest at 45∘ and 135∘. From Fig. 3, it is found that 2D NEO response obtained from all directions has less error due to the rotation compared with 2D NEO response obtained from x and y directions. Therefore, the second possibility is selected to extend the NEO operator in 2D.
Fig. 2.
Visualization of NEO responses. a ROI containing microcalcification. b 2D NEO response in all directions of ROI in (a). c 2D NEO response only in x and y directions of ROI in (a). d ROI containing microcalcification rotated by 45∘. e 2D NEO response in all directions of rotated ROI in (d). f 2D NEO response only in x and y directions of rotated ROI in (d)
Fig. 3.

Plot showing absolute error vs. angle of rotation for 2D NEO response in all directions and 2D NEO response only in x and y directions
Since microcalcifications are of different sizes, a multiscale approach is applied to enhance different-sized microcalcifications. The response of multiscale 2D NEO can be obtained by combining the individual response of 2D NEO at various scales. The 2D NEO response at the dth scale is defined as
where I represents the input image, x and y represent the location of the pixel, and p and q represent the shift in y and x, respectively.
Two techniques are proposed, namely mean multiscale 2D NEO and max multiscale 2D NEO, based on the way the response of 2D NEO are combined over multiple scales. In the mean multiscale 2D NEO technique, the final response is obtained by averaging the individual 2D NEO responses of each scale which is given by:
| 1 |
where d indicates the scale and MaxScale represents the maximum scale used for calculating NEO response which is equal to the maximum size of the microcalcifications.
In the max multiscale 2D NEO technique, the response of multiscale 2D NEO is obtained by taking maximum response over all scales which is given by:
| 2 |
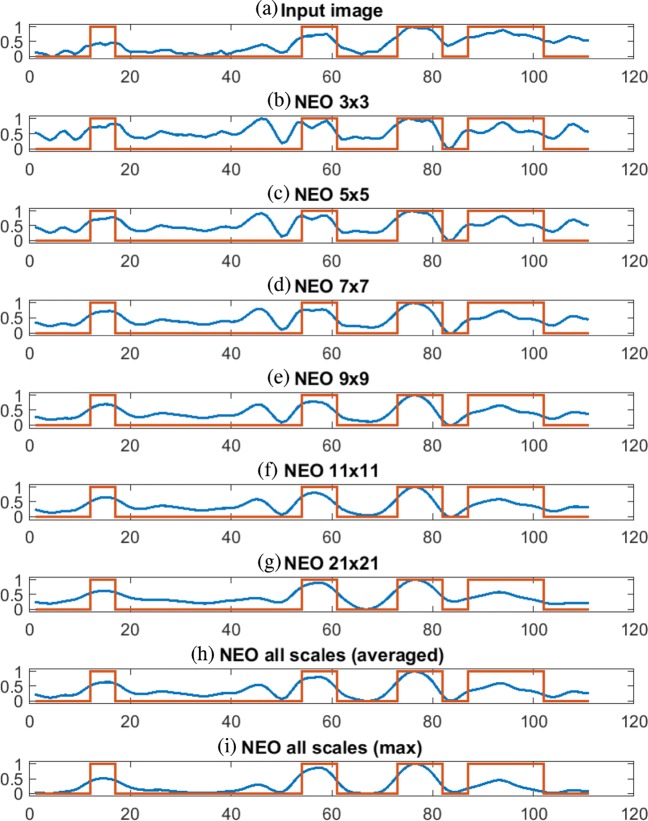
Figure 4 shows the input ROI, corresponding ground truth, and the responses of 2D NEO with various scales ranging from 3×3, 5×5, 7×7, 9×9, 11×11, and 21×21 and combined response of all mentioned scales after box filtering. Figure 4i shows the combined response of NEO across all scales. As shown in Fig. 4c, the response of 2D NEO at the smallest scale of 3×3 is able to detect microcalcifications of size 3 pixels in diameter. The bigger microcalcifications of size greater than 10 pixels in diameter (shown in cyan and yellow color bounding boxes) are split into smaller parts using NEO kernel of size 3×3 and thus unable to detect some of the bigger microcalcifications. The response of 2D NEO at smaller scales appears noisier compared with the response at bigger scales as they are sensitive to the small local variations in intensities of the image. On the other hand, as shown in Fig. 4h, the response of 2D NEO at bigger scales of 21×21 can detect microcalcifications of size greater than 10 pixels in diameter but are less sensitive to the microcalcifications of diameters less than 5 pixels (shown in magenta color bounding box). Same observations are made in Fig. 5, which shows the intensity profile and the NEO responses at various scales along the horizontal line drawn on the ROI shown in Fig. 4a. The ground truth in red color is superimposed on each plot of Fig. 5, which shows the location of microcalcification pixels. Thus, in order to detect the microcalcifications of various sizes, the response of NEO kernels across all scales are combined to get the final response. In the case of mean multiscale NEO, the spurious spikes caused due to the noise present in the image are suppressed, since the response is averaged over all the scales.
Fig. 4.
Responses of 2D NEO filtering at various scales after box filtering on ROI of “C_0063_1.RIGHT_MLO” image of DDSM. a Input ROI. b Ground Truth of the ROI; 2D NEO response for the ROI with kernel size of c 3×3, d 5×5, e NEO 7×7, f NEO 9×9, g NEO 11×11, h NEO 21×21. i NEO all scales averaged (NEO1). j NEO all scales max (NEO2)
Fig. 5.
Linear profile of 2D NEO responses at various scales after box filtering along the horizontal line drawn on ROI shown in Fig. 4a. The red line indicates ground truth of microcalcifications. The blue line indicates image intensity in a input image and 2D NEO responses with kernel size of b 3x3, c 5x5, d 7x7, e 9x9, f 11x11, and g 21x21. h Using all scales (NEO1). i Using all scales (NEO2)
Iterative Thresholding
The preprocessed image is thresholded to get the probable location of microcalcification candidates. The goal of this process is to detect microcalcification clusters with 100% sensitivity by allowing false positive candidates which can be removed in subsequent stages.
In the case of the mean multiscale 2D NEO technique, the threshold is selected such that a preset number of objects, having a higher intensity than the threshold, are detected. The thresholding is started with a value slightly less than the maximum intensity of the pre-emphasized image (NEO output). The image is binarized with this threshold and connected component labeling is done to identify the objects formed by connected pixels. The threshold value is then decreased by a step size if the number of segmented objects is less than the preset number. This procedure is repeated until the number of segmented objects just exceeds the preset number. If and represent the maximum and minimum intensity of the pre-emphasized image respectively, then the step size by which the threshold is decreased is given by . Here, N is the number of threshold levels.
In the case of the max multiscale 2D NEO technique, two nearby peaks may be merged at different scales. It leads to a bigger footprint which disqualifies it as a microcalcification. In order to avoid this, previous thresholding technique is modified. Let the threshold at nth level of thresholding be represented by tn. If at nth level of thresholding, two or more objects (detected at (n − 1)th level) get merge into a single object then those objects are thresholded with the higher threshold tn− 1 while other objects are segmented with threshold tn. This process of multilevel thresholding is continued until we get a preset number of microcalcification candidates. The estimation of preset number for thresholding the image is discussed in Section “Selection of the Preset Number for Thresholding the Microcalcification Candidates”.
Rule-Based False Positive Reduction
Microcalcification appears as a tiny speck in mammograms varying from 0.05 mm to 1 mm in diameter [11]. Thus, most of the false positives objects which are linear in shape and greater than 1 mm can be discarded based on the length of the major axis. Based on these observations, the microcalcification candidates satisfying any one or more of the following rules are removed:
lobj >
Aobj >
Aobj <
where , , and is the maximum length of major axis, maximum area, and the minimum area of the selected objects, respectively. The selection of , , and are discussed in Section “Selection of Thresholds for Rule Based False Positive Reduction”.
Feature Extraction
In rule-based FP reduction step, some of the false positives are reduced, but still, there are plenty of false positives in the binary image. So, the classifier-based false positive reduction is done to reduce remaining false positives. Microcalcifications tend to appear as tiny circular bright spots. Thus, shape- and intensity-based features are used to distinguish microcalcifications from the normal breast region in mammograms. As blood vessels in the mammograms are brighter and have high contrast, some of the broken parts of them are often detected as microcalcifications. Histogram of oriented gradients(HOG) [8] features helps to remove these false positives. Various shape- and texture-based features along with HOG features are extracted from individual segmented objects. All the features are obtained from the local square window, containing the object, with dimension 6 pixels more than the major axis length of the individual object. In total, 38 features are extracted from the pre-emphasized image which are listed in Table 2.
Table 2.
List of all the extracted features
| Type | Feature no. | Feature name |
|---|---|---|
| Intensity | 1 | Foreground-background ratio |
| 2 | Standard deviation obj | |
| 3 | Foreground entropy | |
| 4 | Foreground-background difference | |
| 5 | Mean foreground intensity | |
| Shape | 6 | Area of an object |
| 7 | F3 | |
| 8 | F1 | |
| 9 | compactness | |
| 10 | Fourth moment (F3-F1) | |
| 11 | Elongation | |
| Invariant moments | 12 | Φ1 |
| 13 | Φ2 | |
| 14 | Φ3 | |
| 15 | Φ4 | |
| 16 | Φ5 | |
| 17 | Φ6 | |
| 18 | Φ7 | |
| Haralick features | 19 | Information measure 1 |
| 20 | Information measure 2 | |
| 21 | Sum average | |
| 22 | Correlation | |
| 23 | Inverse difference moment | |
| 24 | Energy | |
| 25 | Sum Entropy | |
| 26 | Sum of the squares | |
| 27 | Sum variance | |
| 28 | Difference variance | |
| 29 | Entropy | |
| 30 | Difference entropy | |
| 31 | Contrast | |
| HOG features | 32 | Mean of HOG bins |
| 33 | HOG bin 1 | |
| 34 | HOG bin 2 | |
| 35 | HOG bin 3 | |
| 36 | HOG bin 4 | |
| 37 | Standard deviation of HOG bins | |
| 38 | Kurtosis of HOG bins |
The list of 38 features and their definitions are given below:
Mean foreground intensity (μf): Mean intensity of segmented objects.
Standard deviation: Standard deviation of the intensities within the segmented object region.
- Foreground-background ratio: It is given by
where μf is the mean intensity of segmented objects and μb is the mean intensity of the background - Foreground-background difference: It is given by
Foreground Entropy: The foreground entropy is the entropy of the intensities within the segmented object region.
Area: Number of pixels present in the segmented objects.
- Compactness: Compactness of segmented object is calculated as follows
- Shape moments: Shape moments proposed by Shen et al. [35] are computed for each segmented object. These moments are defined as:
where
and z[i],i = 1,2,...,N are the Euclidean distances between centroid and the contour pixels of the corresponding segmented object. - Elongation: It is defined as:
where “Major axis length” and “Minor axis length” are computed from eigenvalues of the segmented object. Invariant moments: 7 Invariant moments [13] are calculated within the local window centered at the centroid of the object.
Haralick features: 13 Haralick features [17] are extracted to get local texture information.
HOG-based features: HOG features [8] help to segregate microcalcifications and curvilinear segmented objects. Note that the HOG features are not computed by dividing the complete image into blocks and cells. Instead, the histogram of oriented gradients is computed from local window centered at the centroid of the object. The size of the window is the same as that used for Haralick features. The histogram is quantized into four bins. Also, the mean, standard deviation, and kurtosis values of these four Histogram bins are computed for each segmented object.
Feature Selection
The minimum redundancy maximum relevance (mRMR), proposed by Ding and Peng [10], is used for selecting the relevant features in our experiments. This technique selects the set of features that minimizes the redundancy among individual features and maximizes the relevance between feature and target vector. First, the features are ranked by giving scores to each feature depending on its redundancy with other features and its relevance with the target vector. The forward search is then performed using support vector machines (SVM) classifier and the first K features are selected from the ranked feature list. The K features are selected which maximizes the objective function of balanced accuracy by Velezet al. [38] and is defined as Accb = (sensitivity + specificity)/2. Since accuracy gives overestimated values in case of data imbalance, the balanced accuracy is used as a criterion function.
Handling Data Imbalance Problem
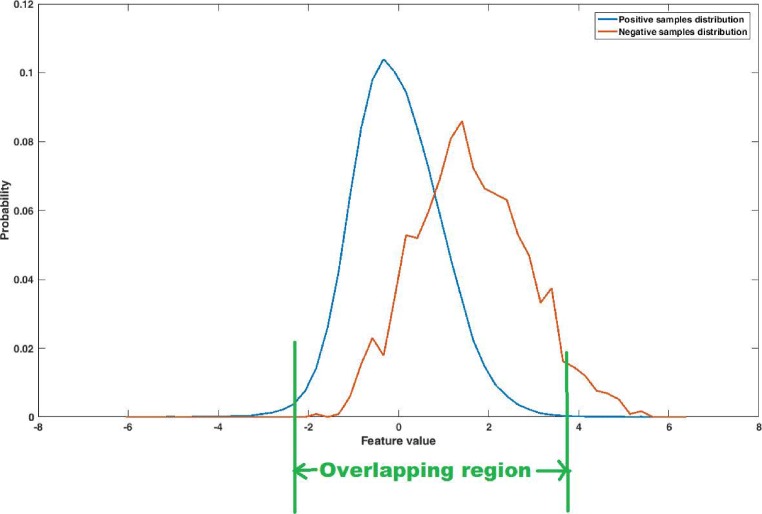
As the number of microcalcification objects is very less as compared with the number of false positive objects, the problem of data imbalance arises. Classifier tends to get biased to the majority class (negative class) samples leading to the reduction of true positives. In the training set, the ratio of positive class to negative class samples is approximately 1:80, 1:20, and 1:90 for the DDSM, PGIMER-IITKGP, and INbreast databases, respectively. In this study, we have proposed a novel majority class data reduction method to handle the data imbalance problem. The performance of SVM classifier can be improved by training it with the samples which are difficult to classify or the samples which lies near the decision boundary [11]. Based on this idea, a simple data reduction technique is proposed which reduces the number of majority class samples (negative class samples). The imbalance of data is reduced by considering only the samples of the majority class (negative class) which have all their features in the overlapping region of probability distributions of positive and negative samples. Thus the majority class samples having any feature lying in the non-overlapping region, are discarded as shown in Fig. 6. The samples are randomly chosen from the reduced majority class (negative class) such that there are equal number of samples from both the classes.
Fig. 6.
Distribution of positive and negative samples
Classification
The SVM [7] classifier with radial basis function kernel is trained using the proposed set of features which helps in reduction of false positives while preserving the true positive objects. The kernel function parameters like Gaussian width (σ) and soft margin constant (C) are determined by performing grid search. The grid search is performed using training data of the 5-fold cross validation. The 2-fold cross validation is applied on training data, and the paired values of σ and C which produce the highest average cross validation accuracy are selected. The values of σ and C for each fold of DDSM, INbreast, and PGIMER-IITKGP mammogram databases are given in Tables 4–9 in the Supplementary Material.
Nearest Neighbor Clustering
Microcalcification clusters are clinically significant, unlike the isolated ones. Thus, the proposed framework is focused on the detection of microcalcification clusters. Since microcalcification cluster is said to be detected if 3 or more number of microcalcifications are detected within 1 square cm region, a single link clustering with a maximum nearest neighbor distance of 0.5 cm is incorporated to cluster the detected objects [41]. The clusters containing less than three objects are discarded.
Evaluation Criteria for Microcalcification Cluster Detection
The convex hull is obtained from detected cluster for categorizing the clusters as true positive (TP) or false positive (FP) clusters. The evaluation criteria are set by radiologist AS which is in-line with the article by Kallergi et al. [19]. The detected cluster is said to be a true positive cluster if the following criteria are met:
The centroid of the detected cluster should lie inside the cluster marked by the radiologist as the ground truth.
The area of the convex hull of a detected cluster should not exceed five times the cluster area marked by the radiologist.
Results
The performance of the proposed methods is evaluated with 5-fold cross validation. The mammograms with and without MC clusters, from selected dataset, are split into 5 folds. The splitting of selected dataset is done patient-wise, i.e., all the mammograms of same patient will be in the same fold. In each round, one fold each from the mammograms with MC clusters and the mammograms without MC clusters is selected for testing and the remaining four folds from each are selected for training. In the case of DDSM, a uniform distribution of subtlety levels for microcalcification clusters is maintained in each fold. For the test data in each fold, the parameters and features are selected using corresponding set of training data. The selection of parameters along with their effect on performance followed by the performance of the proposed methods has been discussed in Sections “Selection of Scales of 2D NEO”, “Selection of the Preset Number for Thresholding the Microcalcification Candidates”, “Selection of Thresholds for Rule Based False Positive Reduction” to “Reduction of False Positives using SVM Classifier”.
Selection of Scales of 2D NEO
The pre-emphasis step enhances the contrast between the microcalcifications and background tissues using multiscale 2D NEO. The maximum scale used for calculating 2D NEO response corresponds to maximum size of the microcalcifications (1 mm). The value of MaxScale in Eqs. (1) and (2) is given by:
where Max_MC_size is the maximum size of the microcalcification in pixels corresponding to 1 mm, which is given by:
where res is the resolution of the input image in millimeter. The above formula is adjusted such that Max_MC_size is always odd since it corresponds to the maximum kernel size for the calculation of 2D NEO.
Selection of the Preset Number for Thresholding the Microcalcification Candidates
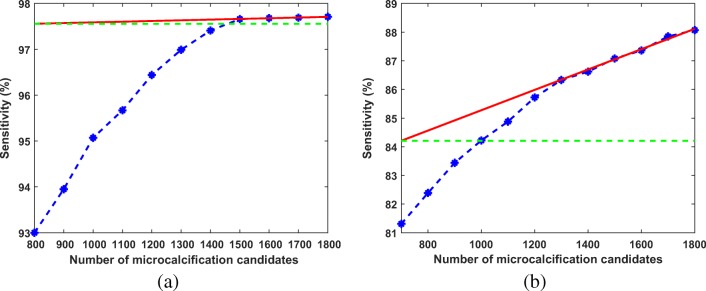
The preprocessed image is thresholded using iterative thresholding. The threshold is decreased from maximum to minimum intensity of pre-emphasized image in “N” number of steps. The value of “N” is chosen as 1000 in our experiments (The effect of N on sensitivity and FP per image is given in Section 1 of the Supplementary Material). The preprocessed image is thresholded in such a way that some preset number of objects having the higher intensities are segmented. The number of microcalcification candidates was determined from the training set of 5-fold validation by analyzing the sensitivity and the number of segmented objects. The sensitivity of individual microcalcifications vs. number of microcalcification candidates are shown respectively in Fig. 7a and b for DDSM and PGIMER-IITKGP database, respectively. The sensitivity of the microcalcification detection increases with the number of microcalcification candidates. Two approaches are followed to determine the preset number of microcalcification candidates to be thresholded, depending on whether the curve saturates. In order to determine whether the curve is saturated, the angle of inclination of the line fitted on last three points is calculated. If the angle of inclination of the line is less than 10 degrees then the curve is considered in saturation. As shown in Fig. 7a, the curve saturates for the number of microcalcification candidates greater than 1500.
Fig. 7.
A plot of sensitivity of individual microcalcifications versus number of microcalcification candidates. The red line is fitted using the last three points in the plot. The green line is the reference line for measuring the angle of inclination of the red line a for DDSM and b for PGIMER-IITKGP database
A second approach is used to find the knee point of the curve when it does not saturate. Figure 7b shows one of the case where the curve does not saturate as there is small decrease in curvature even after 1500 microcalcification candidates, unlike the one shown in Fig. 7a. In Fig. 8, a second-order polynomial (c1 in red color) is fitted through all the points. A line (l1 in orange color) joining the first and last point is drawn. Two straight lines (l2 in purple and l3 in green color in Fig. 8) are fitted on first three points and last three points, respectively. From the point of intersection (p1) of the lines l2 and l3, a perpendicular (l4 in cyan color) is drawn on line l1. It cuts the curve (c1) at a point p2. The number of microcalcification candidates is selected from the nearest neighbor of p2. In Fig. 8, the number of candidate objects should be selected as 1100.
Fig. 8.

This figure shows plot of sensitivity of individual microcalcifications versus number of microcalcification candidates for PGIMER-IITKGP database. This figure also shows how to find out the knee point (p2) and the nearest point (p3) indicating the number of microcalcification candidates which should be selected for 100% sensitivity
Selection of Thresholds for Rule Based False Positive Reduction
After the probable microcalcification candidate selection, the ratio of the number of microcalcifications to the number of false positives is 1:120, 1:21, and 1:100 for DDSM, PGIMER-IITKGP, and INbreast databases, respectively. Due to such large imbalance in the number of samples in two classes, the classifier is not trained appropriately and it gets biased towards majority class. Thus, there is a need to reduce false positives for reducing the imbalance between the classes. Based on the clinical knowledge, some rules are derived from the shape and appearance of microcalcifications which are mentioned in the Section “Rule-Based False Positive Reduction”. The maximum size of the microcalcification in mammograms is 1 mm [5, 11]. Thus, the false positive objects having major axis length greater than maximum length in pixels () are eliminated. The value of , corresponding to 1 mm, is given by:
where “res” is the resolution of the input image in millimiter.
The threshold on maximum area () for rejecting the false positive objects is given by:
Most of the objects having an area less than 3 pixels are due to noise present in the image [5, 43]. So, the minimum area of microcalcification () is selected as 3 pixels for the elimination of very small detected objects.
Reduction of False Positives using SVM Classifier
For the comparison of the proposed techniques with existing literature, some of the automated techniques for the detection of microcalcification clusters are implemented for bench-marking. The performances of proposed techniques, i.e., mean multiscale 2D NEO and max multiscale 2D NEO, are compared with competing techniques by El-Naqa et al. [11], Zhang et al. [44], and Karale et al. [20]. Mordang et al. [24] proposed a deep learning–based technique for the detection of microcalcification clusters. In the said method, the regions of interest or patches of size 13×13 pixels are manually cropped and are divided into training and test set for performance evaluation. Thus, the said method is semi-automated and cannot be compared directly with the proposed methods. In order to compare the performance of the proposed techniques with competing technique, maximum sensitivity and the corresponding FP per image are calculated for each fold of 5-fold cross-validation for the individual technique. The average of the maximum sensitivities and the average of FP per image is computed across 5-folds. The comparative performance of the proposed methods in terms of the average maximum sensitivity and the average FP per image with standard deviation is shown in Table 3.
Table 3.
Comparative performance of proposed methods in terms of average maximum sensitivity and the average FP per image with standard deviation
| Database | Techniques | No. of MC clusters | No. of MC clusters detected | Average maximum sensitivity (%) | Average FP per image with standard deviation |
|---|---|---|---|---|---|
| DDSM | El-Naqa et al. [11] | 100 | 99 | 99 | 8.51 ± 2.68 |
| Karale et al. [20] | 100 | 92 | 92 | 3.79 ± 0.86 | |
| Zhang et al. [44] | 100 | 73 | 73 | 8.37 ± 2.45 | |
| mean multiscale 2D NEO | 100 | 100 | 100 | 2.59 ± 1.47 | |
| max multiscale 2D NEO | 100 | 99 | 99 | 3.35 ± 1.89 | |
| PGIMER-IITKGP | El-Naqa et al. [11] | 76 | 71 | 92.89 | 1.59 ± 1.09 |
| Karale et al. [20] | 76 | 72 | 94.43 | 0.91 ± 0.45 | |
| Zhang et al. [44] | 76 | 74 | 97.29 | 3.14 ± 2.67 | |
| mean multiscale 2D NEO | 76 | 76 | 100 | 0.68 ± 0.62 | |
| max multiscale 2D NEO | 76 | 76 | 100 | 2.0 ± 2.81 | |
| INbreast | El-Naqa et al. [11] | 26 | 26 | 100 | 4.25 ± 3.05 |
| Karale et al. [20] | 26 | 25 | 97.14 | 2.13 ± 2.2 | |
| Zhang et al. [44] | 26 | 25 | 97.14 | 2.29 ± 1.79 | |
| mean multiscale 2D NEO | 26 | 26 | 100 | 1.78 ± 1.2 | |
| max multiscale 2D NEO | 26 | 25 | 97.14 | 0.67 ± 0.31 |
In the case of mean-multiscale 2D NEO, we could achieve the best results of 100% sensitivity with 2.59, 0.68, and 1.78 average FP per image for the DDSM, PGIMER-IITKGP, and INbreast databases, respectively. The max-multiscale 2D NEO outperforms previous competing techniques in the cases of INbreast and PGIMER-IITKGP mammogram database.
The results obtained for the technique by Karale et al. in this study are similar to the results reported in their work whereas the results obtained for the techniques by El-Naqa et al. and Zhang et al. are lower than the results reported in their work. The deviation in the simulated results for competing techniques could be due to change in evaluation criteria and difference in the set of images used for the experiment. We have used a more realistic criteria which are set by radiologist for the evaluation of TP and FP clusters. In the case of the criteria followed by El-Naqa et al., the detected cluster is considered as TP cluster if at least 3 true microcalcifications are detected within an area of 1 cm2. There is no upper limit on the detected cluster area for considering the detected cluster as TP, which causes overestimation of the performance. The criteria chosen in our study penalizes detected clusters whose area is unreasonably large. Thus, the clusters whose area is more than five times the area of the ground truth cluster are considered as FP clusters. Zhang et al. have not mentioned the evaluation criteria for considering the detected cluster as TP or FP cluster.
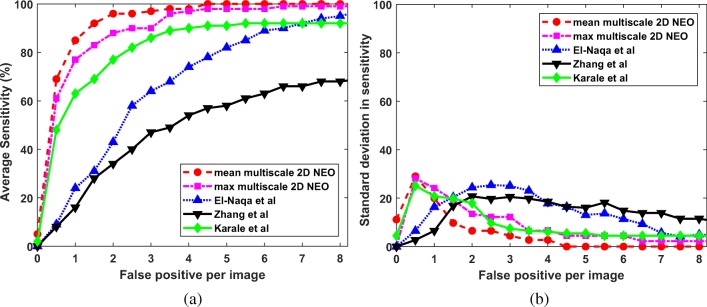
Since we are interested in the detection of microcalcification clusters, the results are computed in terms of true positive and false positive clusters. The estimation of metrics like specificity, accuracy, and false positive fraction is not possible, as it requires the number of negative clusters which are not known a priori. So, the ROC analysis is not suitable for the performance evaluation of the proposed techniques. In this study, the FROC analysis is done to compare the performance of the proposed techniques with the competing techniques. For the computation of FROC response, the average sensitivity is calculated across 5-folds at various FP per image. The average sensitivity at the interval of 0.5 FP per image is given in Figs. 9a, 10a, and 11a for DDSM, PGIMER-IITKGP, and INbreast databases respectively. The corresponding standard deviation in sensitivity is given in Figs. 9b, 10b, and 11b.
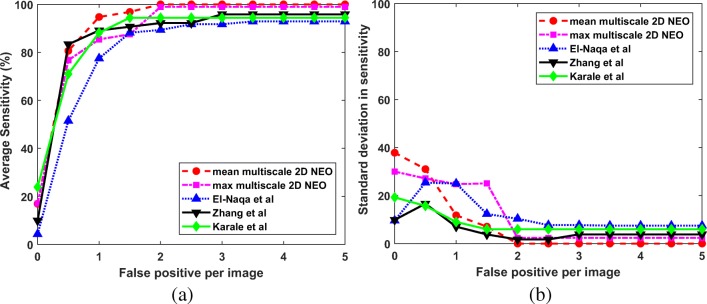
Fig. 9.
a FROC plots and b standard deviation of sensitivity values for the proposed techniques (mean multiscale 2D NEO and max multiscale 2D NEO) with El-Naqa et al., Zhang et al., and Karale et al., for the DDSM
Fig. 10.
a FROC plots and b standard deviation of sensitivity values for the proposed techniques (mean multiscale 2D NEO and max multiscale 2D NEO) with El-Naqa et al., Zhang et al., and Karale et al., for the PGIMER-IITKGP mammogram database
Fig. 11.
a FROC plots and b standard deviation of sensitivity values for the proposed techniques (mean multiscale 2D NEO and max multiscale 2D NEO) with El-Naqa et al., Zhang et al., and Karale et al., for the INbreast database
From Fig. 9a, the mean multiscale 2D NEO has high mean sensitivity values compared with competing techniques at various FP per image. As shown in Fig. 9b, the mean multiscale 2D NEO and max multiscale 2D NEO have higher values of standard deviation in sensitivity compared with competing techniques up to 1.5 FP per image and gradually decreases to zero at 4 FP per image. Thus, the proposed methods are more robust at higher sensitivity values compared with competing techniques. Similar observations can be made from Fig. 10a, b. As shown in Fig. 11a and b, mean multiscale 2D NEO has zero standard deviation at 3.5 or more FP per image.
The average sensitivity along with standard deviation values obtained by individual techniques at various FP per image for DDSM, PGIMER-IITKGP, and INbreast databases are given in Tables 1, 2, and 3, respectively, in the Supplementary Material.
The technique by El-Naqa et al. used high pass filtering as preprocessing technique and done pixelwise classification using the 7×7 local window on high pass filtered output. The method did not used any shape-based, intensity-based features to reduce FP. Thus, the technique has more FP clusters at high sensitivity. The technique by Zhang et al. proposed a preprocessing technique based on morphological image processing but the technique does not use any machine learning algorithm to further reduce the false positives. Karale et al. proposed modified unsharp masking as preprocessing technique and use random undersampling to handle data imbalance problem which lead to reduction in sensitivity. Thus, the method could not achieve 100% sensitivity in this study. The performance of proposed mean multiscale 2D NEO technique is better compared with the competing techniques due to (a) the improvement in the pre-emphasis technique, (b) elimination of false positives based on clinical knowledge of microcalcification size, (c) use of intensity-, shape-, and texture-based features to classify microcalcifications and normal objects using SVM, (d) use of novel majority class data reduction technique to cope with data imbalance problem efficiently. The heuristic parameters (viz. maximum scale for obtaining NEO response, preset number to terminate the iterative thresholding process, and the thresholds used for elimination of false positive objects) are selected by data-driven approach given in Section “Selection of Scales of 2D NEO”, “Selection of the Preset Number for Thresholding the Microcalcification Candidates”, and “Selection of Thresholds for Rule Based False Positive Reduction”, making it easy to adapt for an unknown databases.
Figures 12, 13, and 14 show example of the missed cases by competing methods from the PGIMER-IITKGP mammogram database, DDSM, and INbreast database, respectively. As shown in Fig. 12e, the technique by El-Naqa et al. is able to detect three individual microcalcifications but they are not present in 1 square cm area and hence the cluster is missed. Zhang et al. has detected a cluster whose area is greater than 5 times the area of cluster in ground truth and hence the detected cluster is considered as false positive, as shown in Fig. 12g. Figures 12f, 13e, g, and 14e–g shows the missed cases where the number of microcalcifications detected is less than 3 and hence the clusters are missed.
Fig. 12.
Comparative results of missed case from the PGIMER-IITKGP database for a original image, b ground truth, c mean multiscale 2D NEO, d max multiscale 2D NEO, e El-Naqa et al., f Karale et al., and g Zhang et al.
Fig. 13.
Comparative results of missed case from the DDSM for a Original image, b Ground truth, c mean multiscale 2D NEO, d max multiscale 2D NEO, e El-Naqa et al., f Karale et al., g Zhang et al.
Fig. 14.
Comparative results of missed case from the INbreast database for a Original image, b Ground truth, c mean multiscale 2D NEO, d max multiscale 2D NEO, e El-Naqa et al., f Karale et al., g Zhang et al.
Discussion
In this study, we have three major contributions. The first contribution is the pre-emphasis using multiscale 2D NEO to pre-emphasize microcalcifications and suppress the high-intensity objects in the background. Thus, it helps to detect all the true positive MC clusters in the preprocessing step. The second contribution is the use of HOG, intensity-based, shape-based, and texture-based features for segregating microcalcifications from false positive objects. The third contribution is in handling data imbalance problem. The novel majority class data reduction technique is proposed which reduces the number of majority class samples based on the distribution of majority and minority class samples.
The proposed algorithm can be compared with various automated algorithms in terms of sensitivity and FP per image. Peng et al. [30] used stochastic resonance for the detection of MC clusters and reported an average sensitivity of 94% with 3.12 FP per image on 75 images from DDSM and MIAS databases. Oliver et al. [28] proposed knowledge-based approach for the detection of MC clusters and reported 90% sensitivity with FP per image ranging between (3.23,5.52) on MIAS and (3.54,4.09) on private database. The results of the said method are reported on 322 and 280 images of MIAS and private database, respectively. Nakayama et al. [26] proposed eight multiscale features based on eigenvalue values of Hessian matrix for the detection of MC clusters and achieved a sensitivity of 100% with 0.98 FP per image. The method was tested on 1200 images with 600 normal and 600 abnormal images from DDSM. The comparison of the method with proposed technique requires the ground truth of blood vessels which is not publicly available. Blood vessels in the mammograms are difficult to identify unless it has calcium deposition around its boundaries. Thus, the technique by Nakayama et al. is not suitable for implementation to compare with proposed techniques. Linguraru et al. [22] proposed a biologically inspired contrast stretching followed by foveal segmentation and reported a sensitivity of 100% with FP per image slightly greater than two on DDSM with 58 images with MC clusters and 24 normal images. Note that the performance of the microcalcification detection technique highly depends on evaluation criteria and the set of the images used in the study.
The proposed mean multiscale 2D NEO method achieved 100% sensitivity with a significantly lower number of false positives per image on DDSM, PGIMER-IITKGP, and INbreast databases. The number of images (without microcalcification clusters) detected without any false positive cluster is 48 out of 100, 43 out of 50, and 178 out of 389 for DDSM, PGIMER-IITKGP, and INbreast database, respectively. This constitutes 48%, 86%, and 45.68% savings for radiologists in reading the images without microcalcification clusters for DDSM, PGIMER-IITKGP, and INbreast database, respectively.The recall rates of microcalcifications in screening mammograms are 1.7%, 1.82%, 0.67% for 0.42% in Germany, USA, Netherlands, and Australia, respectively [40]. Thus, the proposed mean multiscale 2D NEO method, when used as a screening tool, can play a crucial role in reducing a significant amount of workload of the radiologists.
The proposed max multiscale 2D NEO is able to achieve 100% sensitivity on only PGIMER-IITKGP mammogram database. Although the proposed mean multiscale 2D NEO method achieves 100% sensitivity in detection of microcalcification cluster on all the three databases used in the study, the method fails to achieve 100% sensitivity for detecting individual microcalcifications. In some cases where the number of microcalcifications in a cluster is less than or equal 6, the proposed methods are able to detect only 3 microcalcifications.
Conclusions
A completely automated technique is proposed for the detection of clustered microcalcifications. A novel multiscale 2D NEO–based filtering technique is used as a preprocessing step for enhancing the contrast between microcalcification and background in the mammogram. The preprocessing step detects all microcalcification clusters in the first stage. Several intensity-, texture-, shape-, and HOG-based features are used for reducing false positives in classification stage. A new majority class data reduction technique is proposed to handle data imbalance efficiently. The sensitivity of 100% is achieved with moderate false positives per image for the three databases used in this study. Apart from the normal use of CAD as a second reader, the mean multiscale 2D NEO can act as a screening tool. It might eliminate considerable portion of the normal images from the work-list and thereby reduces the workload of the radiologists.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Footnotes
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Bray F, Ferlay J, Soerjomataram I, Siegel RL, Torre LA, Jemal A. Global cancer statistics 2018: Globocan estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J Clin. 2018;68(6):394–424. doi: 10.3322/caac.21492. [DOI] [PubMed] [Google Scholar]
- 2.Bulas D, Shah N. International pediatric radiology education: who should be trained, and how? Pediatr Radiol. 2014;44(6):639–641. doi: 10.1007/s00247-014-2910-7. [DOI] [PubMed] [Google Scholar]
- 3.Chen Z, Strange H, Oliver A, Denton ERE, Boggis C, Zwiggelaar R. Topological modeling and classification of mammographic microcalcification clusters. IEEE Trans Biomed Eng. 2015;62(4):1203–1214. doi: 10.1109/TBME.2014.2385102. [DOI] [PubMed] [Google Scholar]
- 4.Cheng H, Cai X, Chen X, Hu L, Lou X. Computer-aided detection and classification of microcalcifications in mammograms: a survey. Pattern Recogn. 2003;36(12):2967–2991. [Google Scholar]
- 5.Ciecholewski M. Microcalcification segmentation from mammograms: a morphological approach. J Digit Imaging. 2017;30(2):172–184. doi: 10.1007/s10278-016-9923-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cox RF, Hernandez-Santana A, Ramdass S, McMahon G, Harmey JH, Morgan MP. Microcalcifications in breast cancer: novel insights into the molecular mechanism and functional consequence of mammary mineralisation. Br J Cancer. 2012;106(3):525–537. doi: 10.1038/bjc.2011.583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cristianini N, Shawe-Taylor J. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods. Cambridge: Cambridge University Press; 2000. [Google Scholar]
- 8.Dalal N, Triggs B: Histograms of oriented gradients for human detection.. In: IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), vol 1. IEEE, 2005, pp 886–893
- 9.Dengler J, Behrens S, Desaga J. Segmentation of microcalcifications in mammograms. IEEE Trans Med Imaging. 1993;12(4):634–642. doi: 10.1109/42.251111. [DOI] [PubMed] [Google Scholar]
- 10.Ding C, Peng H. Minimum redundancy feature selection from microarray gene expression data. J Bioinform Comput Biol. 2005;3(02):185–205. doi: 10.1142/s0219720005001004. [DOI] [PubMed] [Google Scholar]
- 11.El-Naqa I, Yang Y, Wernick MN, Galatsanos NP, Nishikawa RM. A support vector machine approach for detection of microcalcifications. IEEE Trans Med Imaging. 2002;21(12):1552–1563. doi: 10.1109/TMI.2002.806569. [DOI] [PubMed] [Google Scholar]
- 12.Ferlay J, Soerjomataram I, Dikshit R, Eser S, Mathers C, Rebelo M, Parkin DM, Forman D, Bray F. Cancer incidence and mortality worldwide: sources, methods and major patterns in GLOBOCAN 2012. Int J Cancer. 2015;136(5):E359–E386. doi: 10.1002/ijc.29210. [DOI] [PubMed] [Google Scholar]
- 13.Gonzalez RC, Woods RE. Digital Image Processing. Upper Saddle River: Prentice-Hall; 2002. [Google Scholar]
- 14.Guan PP, Yan H. A hierarchical multilevel thresholding method for edge information extraction using fuzzy entropy. Int J Mach Learn Cybern. 2012;3(4):297–305. [Google Scholar]
- 15.Guo Y, Dong M, Yang Z, Gao X, Wang K, Luo C, Ma Y, Zhang J. A new method of detecting micro-calcification clusters in mammograms using contourlet transform and non-linking simplified pcnn. Comput Methods Programs Biomed. 2016;130:31–45. doi: 10.1016/j.cmpb.2016.02.019. [DOI] [PubMed] [Google Scholar]
- 16.Gurcan M, Yardimci Y, Cetin A, Ansari R. Detection of microcalcifications in mammograms using higher order statistics. IEEE Signal Process Lett. 1997;4(8):213–216. [Google Scholar]
- 17.Haralick RM, Shanmugam K, Dinstein I. Textural features for image classification. IEEE Trans Syst Man Cybern. 1973;3(6):610–622. [Google Scholar]
- 18.Kaiser JF: On a simple algorithm to calculate the energy of a signal.. In: International Conference on Acoustics, Speech, and Signal Processing, ICASSP-90. IEEE, 1990, pp 381–384
- 19.Kallergi M, Carney GM, Gaviria J. Evaluating the performance of detection algorithms in digital mammography. Med Phys. 1999;26(2):267–275. doi: 10.1118/1.598514. [DOI] [PubMed] [Google Scholar]
- 20.Karale VA, Mukhopadhyay S, Singh T, Khandelwal N, Sadhu A: Automated detection of microcalcification clusters in mammograms.. In: SPIE Medical Imaging, vol 10134, 2017, pp 101342r–101342r. International society for optics and photonics. 10.1117/12.2254330
- 21.Kim JK, Park HW. Statistical textural features for detection of microcalcifications in digitized mammograms. IEEE Trans Med Imaging. 1999;18(3):231–238. doi: 10.1109/42.764896. [DOI] [PubMed] [Google Scholar]
- 22.Linguraru MG, Marias K, English R, Brady M. A biologically inspired algorithm for microcalcification cluster detection. Med Image Anal. 2006;10(6):850–862. doi: 10.1016/j.media.2006.07.004. [DOI] [PubMed] [Google Scholar]
- 23.Liu X, Mei M, Liu J, Hu W. Microcalcification detection in full-field digital mammograms with pfcm clustering and weighted svm-based method. EURASIP Journal on Advances in Signal Processing. 2015;2015(1):1. [Google Scholar]
- 24.Mordang JJ, Janssen T, Bria A, Kooi T, Gubern-Mérida A, Karssemeijer N: Automatic microcalcification detection in multi-vendor mammography using convolutional neural networks.. In: International Workshop on Digital Mammography. Springer, 2016, pp 35–42
- 25.Mukhopadhyay S, Ray G. A new interpretation of nonlinear energy operator and its efficacy in spike detection. IEEE Trans Biomed Eng. 1998;45(2):180–187. doi: 10.1109/10.661266. [DOI] [PubMed] [Google Scholar]
- 26.Nakayama R, Uchiyama Y, Yamamoto K, Watanabe R, Namba K. Computer-aided diagnosis scheme using a filter bank for detection of microcalcification clusters in mammograms. IEEE Trans Biomed Eng. 2006;53(2):273–283. doi: 10.1109/TBME.2005.862536. [DOI] [PubMed] [Google Scholar]
- 27.Nam SH, Choi JY: A method of image enhancement and fractal dimension for detection of microcalcifications in mammogram.. In: Proceedings of the 20th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, vol 2. IEEE, 1998, pp 1009–1012. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=745620
- 28.Oliver A, Torrent A, Lladó X, Tortajada M, Tortajada L, Sentís M, Freixenet J, Zwiggelaar R. Automatic microcalcification and cluster detection for digital and digitised mammograms. Knowl-Based Syst. 2012;28:68–75. [Google Scholar]
- 29.Papadopoulos A, Fotiadis DI, Costaridou L. Improvement of microcalcification cluster detection in mammography utilizing image enhancement techniques. Comput Biol Med. 2008;38(10):1045–1055. doi: 10.1016/j.compbiomed.2008.07.006. [DOI] [PubMed] [Google Scholar]
- 30.Peng R, Chen H, Varshney PK. Noise-enhanced detection of micro-calcifications in digital mammograms. IEEE J Sel Top Sign Proces. 2009;3(1):62–73. [Google Scholar]
- 31.Rampun A, Wang H, Scotney B, Morrow P, Zwiggelaar R: Classification of mammographic microcalcification clusters with machine learning confidence levels.. In: 14Th International Workshop on Breast Imaging (IWBI 2018), vol 10718, 2018, p 107181b. International society for optics and photonics
- 32.Rangayyan RM, Ayres FJ, Desautels JEL. A review of computer-aided diagnosis of breast cancer: Toward the detection of subtle signs. J Franklin Inst. 2007;344:312–348. [Google Scholar]
- 33.Rose C, Turi D, Williams A, Wolstencroft K, Taylor C: Web services for the DDSM and digital mammography research.. In: Proceedings of the 8th International Conference on Digital Mammography, IWDM’06. Springer, Berlin, 2006, pp 376–383, 10.1007/11783237_51
- 34.Seth S, Mukhopadhyay S: Multi-level thresholding-based breast segmentation in mammograms.. In: International Conference on Communication, Computers and Devices, Kharagpur, India, 2010
- 35.Shen L, Rangayyan RM, Desautels JL: Shape analysis of mammographic calcifications.. In: Fifth Annual IEEE Symposium on Computer-Based Medical Systems. IEEE, 1992, pp 123–128
- 36.Shin S, Lee S, Yun ID: Classification based micro-calcification detection using discriminative restricted Boltzmann machine in digitized mammograms.. In: SPIE Medical Imaging, 2014, pp 90351l–90351l. International society for optics and photonics
- 37.Soltanian-Zadeh H, Rafiee-Rad F, Pourabdollah-Nejad DS Comparison of multiwavelet, wavelet, haralick, and shape features for microcalcification classification in mammograms. Pattern Recogn. 2004;37(10):1973–1986. [Google Scholar]
- 38.Velez DR, White BC, Motsinger AA, Bush WS, Ritchie MD, Williams SM, Moore JH. A balanced accuracy function for epistasis modeling in imbalanced datasets using multifactor dimensionality reduction. Genetic Epidemiology: the Official Publication of the International Genetic Epidemiology Society. 2007;31(4):306–315. doi: 10.1002/gepi.20211. [DOI] [PubMed] [Google Scholar]
- 39.Wei L, Yang Y, Nishikawa RM, Vernick MN, Edwards A. Relevance vector machine for automatic detection of clustered microcalcifications. IEEE Trans Med Imaging. 2005;24(10):1278–1285. doi: 10.1109/TMI.2005.855435. [DOI] [PubMed] [Google Scholar]
- 40.Wilkinson L, Thomas V, Sharma N. Microcalcification on mammography: approaches to interpretation and biopsy. Br J Radiol. 2016;90(1069):20160594. doi: 10.1259/bjr.20160594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Woods KS, Solka JL, Priebe CE, Doss CC, Bowyer KW, Clarke LP Comparative evaluation of pattern recognition techniques for detection of microcalcifications. Int J Pattern Recognit Artif Intell 841–852, 1993. 10.1117/12.148696
- 42.Yu S, Brown S, Xue Y, Guan L: Enhancement and identification of microcalcifications in mammogram images using wavelets.. In: IEEE International Conference on Systems, Man, and Cybernetics, vol 2, 1996, pp 1166–1171, 10.1109/ICSMC.1996.571251
- 43.Yu S, Guan L. A CAD system for the automatic detection of clustered microcalcifications in digitized mammogram films. IEEE Trans Med Imaging. 2000;19(2):115–126. doi: 10.1109/42.836371. [DOI] [PubMed] [Google Scholar]
- 44.Zhang X, Homma N, Goto S, Kawasumi Y, Ishibashi T, Abe M, Sugita N, Yoshizawa M A hybrid image filtering method for computer-aided detection of microcalcification clusters in mammograms. Journal of Medical Engineering 2013, 2013. http://www.hindawi.com/journals/jme/2013/615254/abs/ [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.