Mekanisk energi \(E\) er gitt ved summen av potensiell energi \(E_p\) og kinetisk energi \(E_k\): \[E = E_p + E_k\]
Nær jordoverflaten er den potensielle energien \(E_p\) gitt ved \(E_p = mgh\), der \(m\) er massen, \(g\) er tyngdens akselerasjon (omtrent 9,81 m/s2), og \(h\) er høyden over et referansepunkt. Den kinetiske energien \(E_k\) er gitt ved \(E_k = \frac{1}{2}mv^2\), der \(v\) er farten.
Det følger fra mekanikkens lover at hvis det ikke er noe energitap på grunn av luftmotstand eller friksjon, så er økningen av kinetisk energi like stor som tapet av potensiell energi. Den mekaniske energien er konstant.
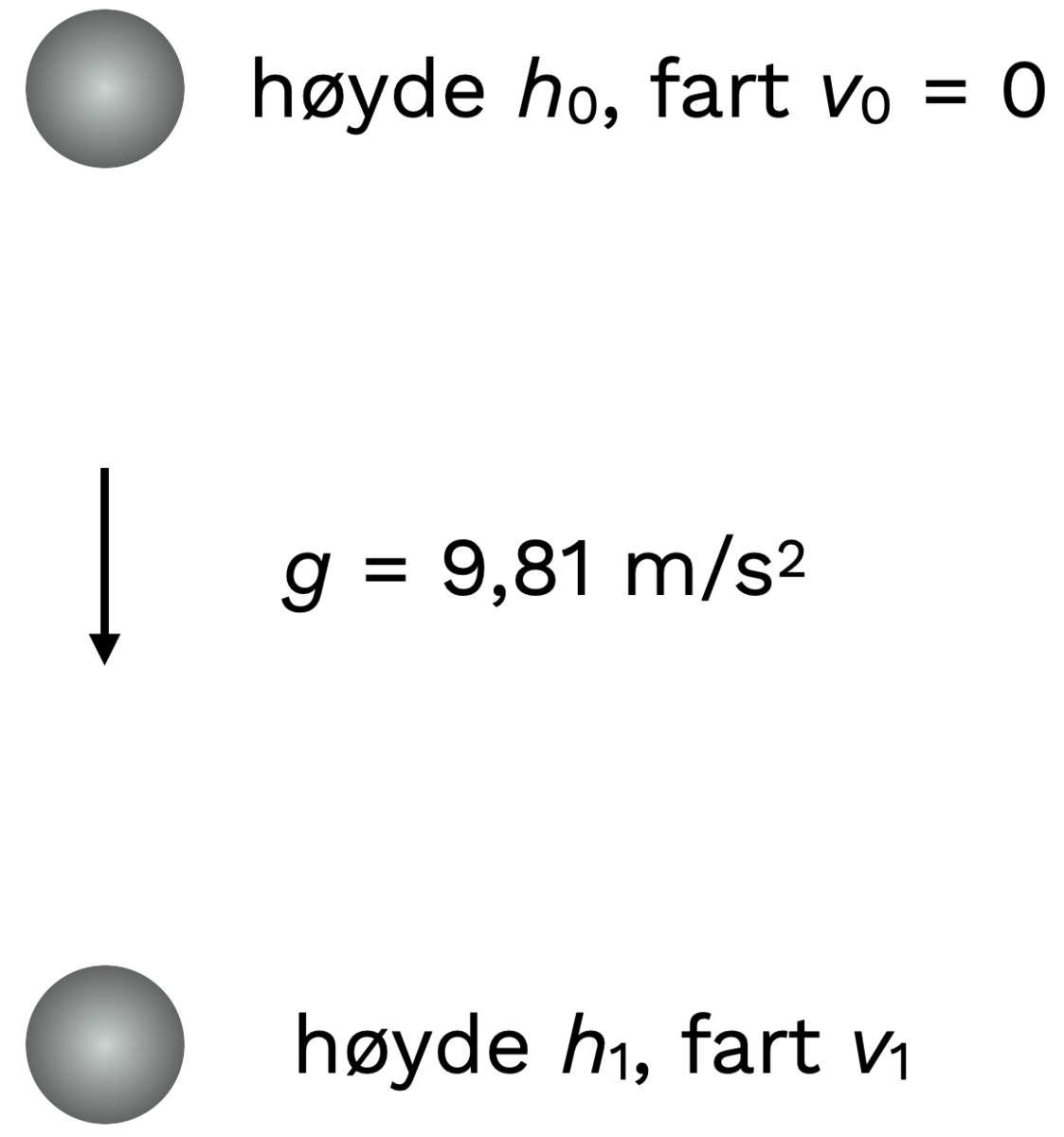
Hvis et legeme med masse \(m\) slippes fra en høyde \(h_0\) og har startfart \(v_0 = 0\), vil den mekaniske energien være \[E_0 = E_{p0} + E_{k0} = mgh_0 + 0 = mgh_0\] Hvis legemet faller uten friksjon eller luftmotstand, vil den mekaniske energien være konstant, og dermed har den hele tiden verdien \(mgh_0\). Ved et senere tidspunkt har legemet falt ned til en høyde \(h_1\), og da er den mekaniske energien gitt ved \[E_1 = E_{p1} + E_{k1} = mgh_1 + \frac{1}{2} mv_1^2\] Siden den mekaniske energien er konstant, har vi at \(E_1 = E_0\), som vil si at \[ mgh_1 + \frac{1}{2} mv_1^2 = mgh_0\]
Hvis vi løser denne ligningen med hensyn på \(v_1\), får vi
\[v_1=\sqrt{2g(h_0-h_1)}\]
Hvis vi setter inn for start- og slutthøyden og tyngdeakselerasjonen, vil vi kunne beregne farten ved høyden \(h_1\). Vi kunne gjort en tilsvarende beregning dersom legemet også hadde en startfart \(v_1\).
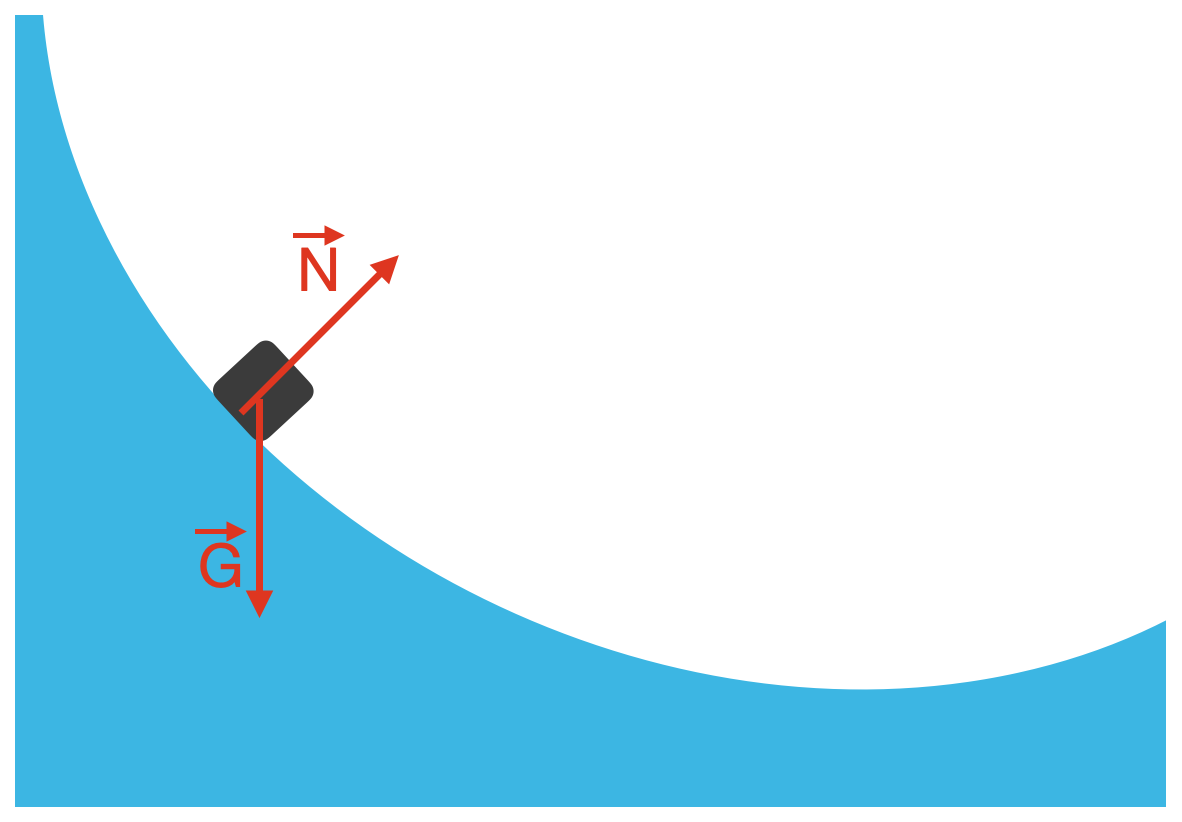
Beregningen over vil være gyldig så lenge det ikke er andre krefter enn tyngden som gjør et arbeid på legemet. Krefter som virker normalt (vinkelrett) på bevegelsesretningen, gjør ikke et arbeid på legemet. Derfor vil beregningen over også være gyldig for et legeme som glir uten friksjon. Kraften fra underlaget virker normalt på bevegelsesretningen, og gjør derfor ikke et arbeid.
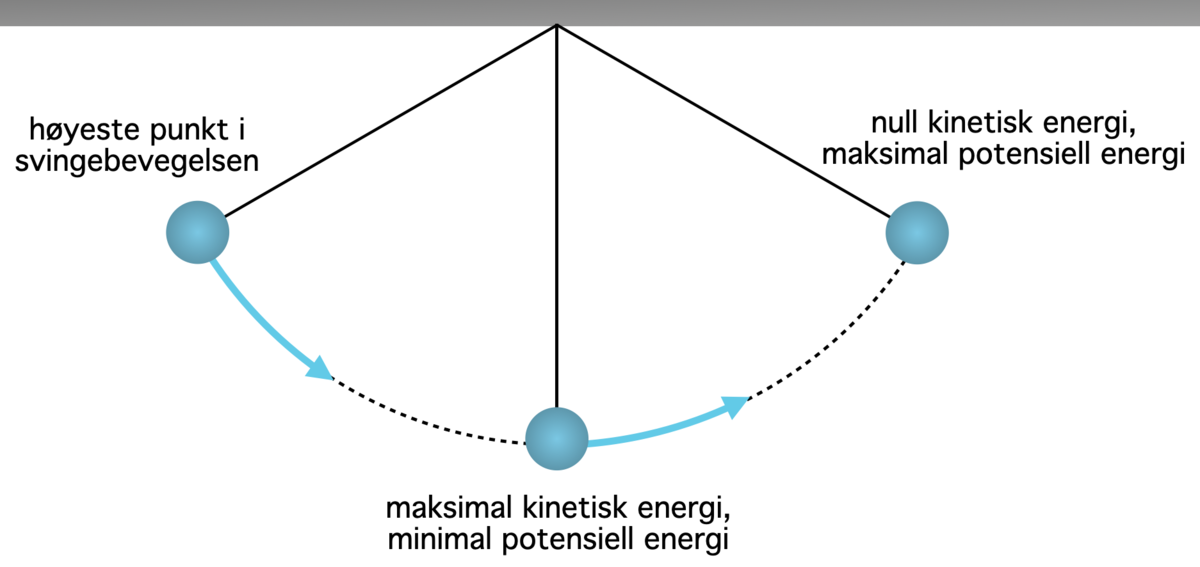
Beregningen vil også være gyldig for en pendel som svinger uten friksjon eller luftmotstand. Da virker kraften fra snora på pendelkula hele tiden normalt på bevegelsesretningen, og denne kraften gjør derfor ikke et arbeid. Den kinetiske energien for pendelen er maksimal i likevektsposisjonen (i bunn av svingebevegelsen) og null ved maksimalt utslag (på toppen av svingebevegelsen).
Den kinetiske energien trenger ikke bare å avhenge av legemets fart, men kan også bestå i for eksempel rotasjonsenergi i et hjul som triller.





Kommentarer (2)
skrev Walther Slørdal
svarte Mari Paus
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.