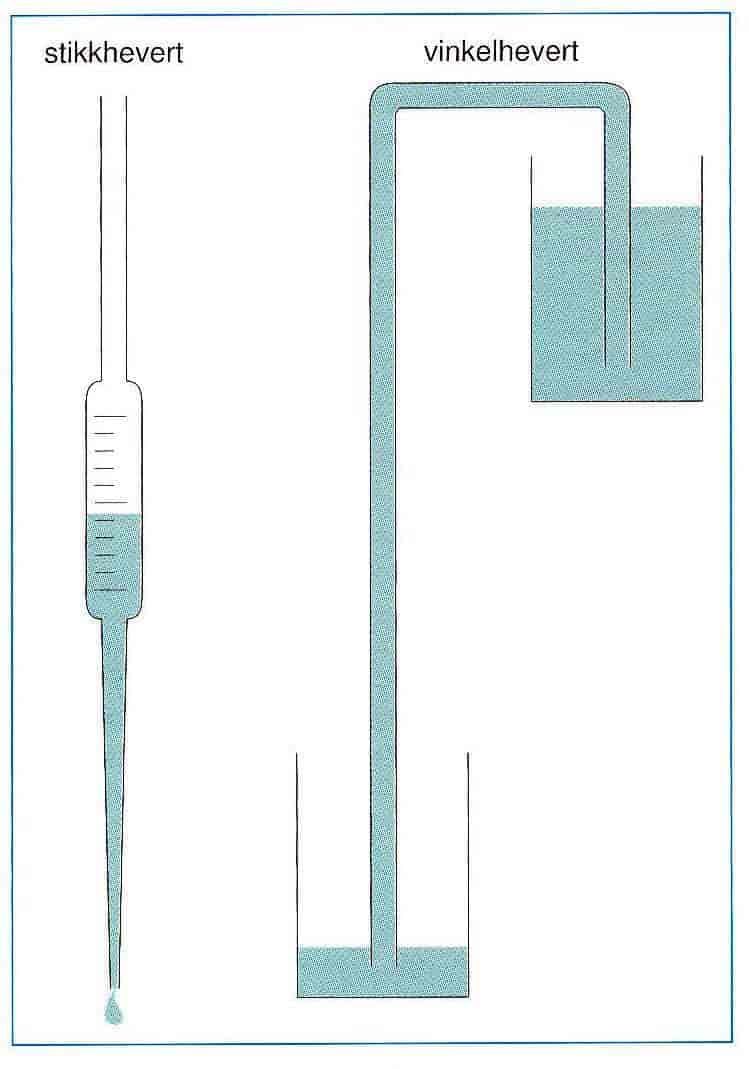
Ein slange blir sett ned i eit kar fylt med væske. Slangen er fylt med væske, slik at væska heng saman inne i slangen. Væska vil då renne frå punkt A til punkt D så lenge tyngdekrafta dreg henne nedover. Dersom det kjem gassbobler i slangen, vil væskestraumen påverkast eller stoppe opp.
Trykket ved vassoverflata (punkt A) er lik det atmosfæriske trykket PA. Det betyr at det statiske trykket inne i slangen ved punktet B er PB=PA-ρg(hB-hA), der ρ er massetettleiken til væska. Her kjem minusteiknet fram fordi vi bevegar oss oppover i væska i forhold til referansenivået (punkt A), som betyr at trykket minkar. På tilsvarande måte kan vi argumentere med at trykket ved punkt D er lik atmosfæretrykket PA, slik at trykket ved punkt C må vere PC=PA-ρg(hC-hD). Sidan hB=hC, veit vi at forskjellen i det statiske trykket mellom punkt B og C må vere PB-PC=ρg(hA-hD). Dette uttrykket viser at det statiske trykket ved B er større enn det ved C, og dessutan at denne trykkforskjellen svarer til høgdeforskjellen mellom vassflata og den nedste enden av slangen. Ein slik trykkforskjell vil ha ein tendens til å prøve å presse væska ut av slangen. Sidan væskemolekyla har ein tendens til henge saman på grunn av kohesjon, vil trykkforskjellen dra med seg væske frå karet, som dermed gradvis blir tømt.
La oss no finne farten til væska ved utløpet av slangen (punkt D). Vi tenkjer oss då at væska har fart null ved punkt A, som er eit godt utgangspunkt dersom tverrsnittsarealet til karet er mykje større enn tverrsnittsarealet til slangen. Då kan vi stille opp Bernoullilikninga for ei straumlinje som passerer punkta A og D som
\[P_{A} + \frac{1}{2}\rho v_{D}^{2} + \rho g h_{D} =P_{A}+\rho g h_{A} \, ,\]
og dette gir farten ved utløpet av slangen som
\[v_{D} =\sqrt{2g(h_{A}-h_{D})} \, .\]
Vi ser no at så lenge utløpet på slangen er under vassoverflata, vil vatnet strøyme ut med ein fart gitt av likninga. Til dømes vil hA-hD= 0.1 m gi vD=1.4 m/s, medan hA-hD= 1 m gir vD=4.4 m/s.
Eit anna interessant spørsmål er kor høgt opp ein kan tenkje seg at toppen av slangen kan vere før heverten sluttar å verke. For å få eit svar på dette, kan ein endå ein gong nytte Bernoullilikninga, men no på eit straumrøyr som går frå punkt A til toppunktet. Vi tenkjer oss at farten i toppunktet er null, fordi væska kan akkurat nå toppunktet øvst i bana si. Trykket her er PT. Det betyr at
\[P_{T} + \rho g h_{T} =P_{A}+\rho g h_{A} \, , \]
slik at den maksimale høgda som heverten kan løfte vatnet, er
\[\Delta h_{max} =h_{T}-h_{A} = \frac{P_{A}-P_{T}}{\rho g} \, . \]
Ein kan tenkje seg at jo høgare vatnet blir løfta i røyret, jo mindre blir trykket. Kjem vatnet høgt nok opp, vil trykket bli mindre enn damptrykket, og kavitasjon oppstår fordi vassmolekyla blir fjerna frå kvarandre. Dette fører til at vatnet startar å danne gassbobler, som igjen fører til at den kontinuerlege vassøyla inne i slangen blir broten. For å få eit rimeleg overslag kan vi vidare setje PT=0. For vatn med massetettleik ρ=998 kg/m3 ved atmosfærisk trykk PA=1.013×105 Pa får vi Δhmax≈10 m. Det vil seie at vatnet kan maksimalt løftast 10 m over vassoverflata.
No må ein likevel vere varsam ved bruk av likninga for maksimal høgd gitt ovanfor. Nyare forsking har nemleg vist at dersom ein kan bli kvitt mest mogleg gass i vatnet, kan dette løftast til Δhmax>15 m i slangen. Slike forsøk tyder på at kavitasjon forårsaka av oppløyst gass er med på å setje avgrensingar for kor høgt vatnet kan løftast. Vidare har eksperiment vist at heverten også kan nyttast i vakuum der PA =0, noko som tyder på at det er spenninga i vassøyla som avgjer kor høgt vatnet kan løftast, og at ein ikkje treng atmosfæretrykk for å få heverten til å verke. Trass i ei historie på over 3000 år, så er heverten framleis ikkje godt nok forstått på mikroskopisk nivå.





Kommentarar (8)
skreiv Knut A. Rosvold
svarte Bjørn Pedersen
skreiv Gunnar Birkeland
Dersom en løfter enden på slangen som står i vann et øyeblikk slik at det kommer luft inn vil det fortsette å renne dersom luftrommet ikke er for langt. Dette mener jeg kommer av at vannet som strømmer ned virker som et stempel og lager undertrykk som er stort nok til å trekke opp vann. Kommer det nok vann til fylle slangen til det kritiske punktet, i høyde med vannspeilet, vil vannet fortsette å strømme.
Kommentarar til artikkelen blir synleg for alle. Ikkje skriv inn sensitive opplysningar, for eksempel helseopplysningar. Fagansvarleg eller redaktør svarar når dei kan. Det kan ta tid før du får svar.
Du må være logga inn for å kommentere.