Fraktal er en geometrisk form som kjennetegnes ved stor kompleksitet og detaljrikdom, dessuten ofte en struktur som er uforandret når målestokken endres.
En fraktal figur vil reprodusere seg selv, det vil si at under forstørrelse vil en enkelt liten del av figuren vise seg nøyaktig lik en tilsvarende del av den opprinnelige figuren.
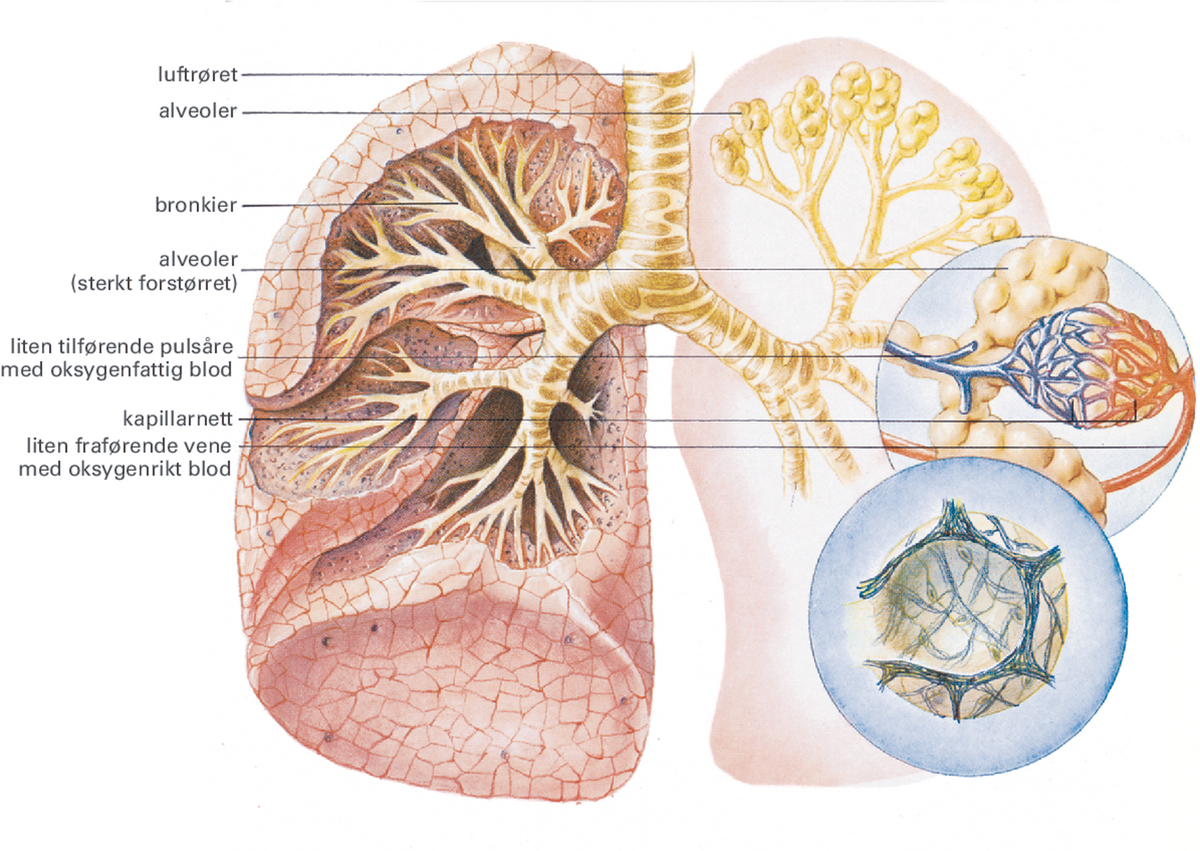
Flere fenomener i naturen har fraktale trekk, for eksempel den geometriske strukturen til et tre, eller til systemer av blodårer og nervebaner i mennesker. Også turbulente strømningsmønstre i væsker har slike trekk.








Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.