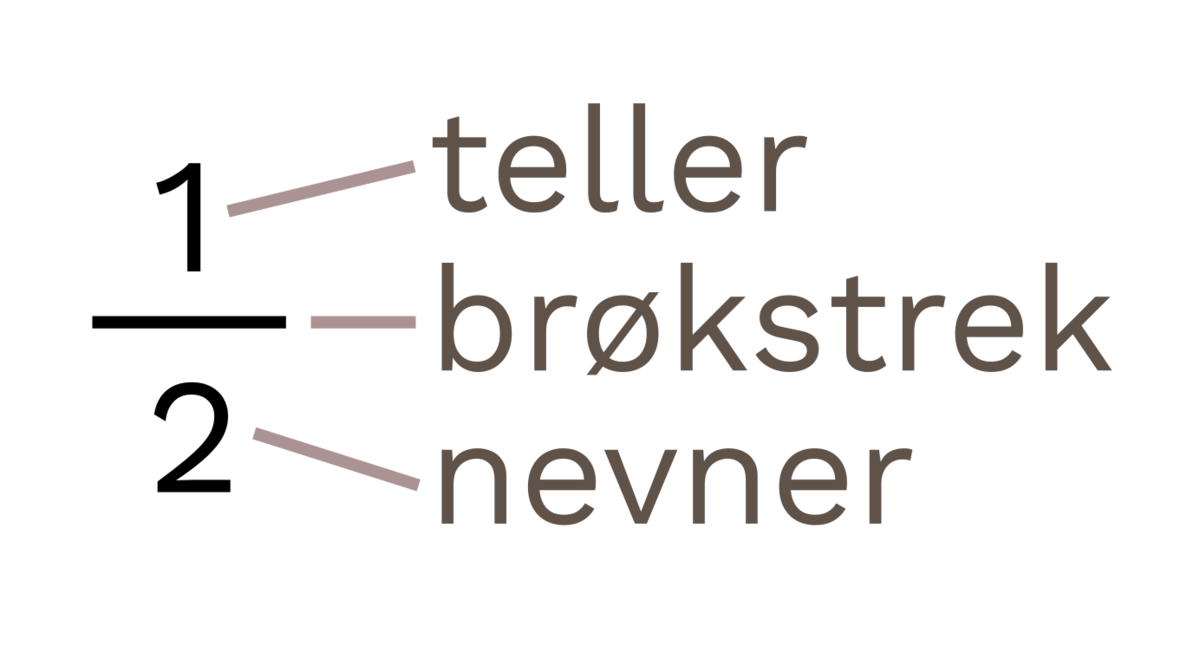
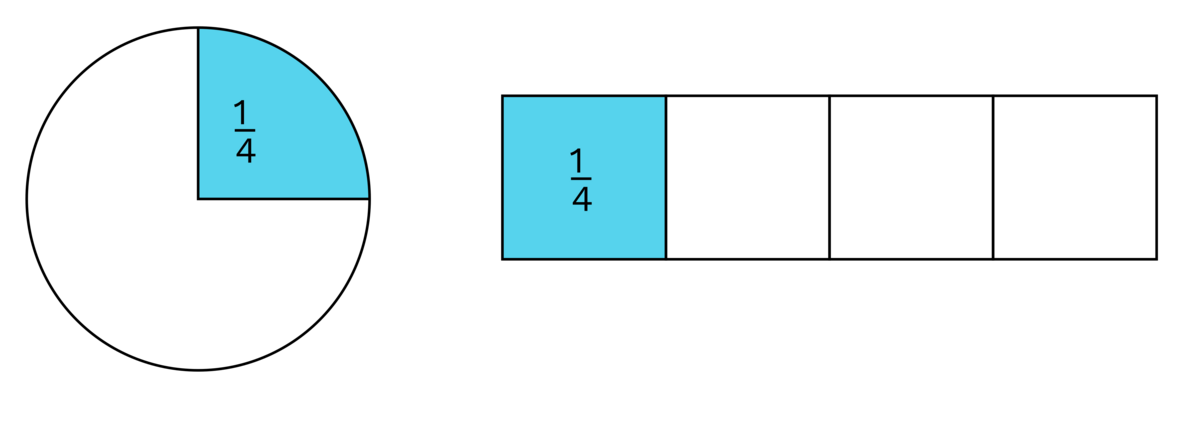
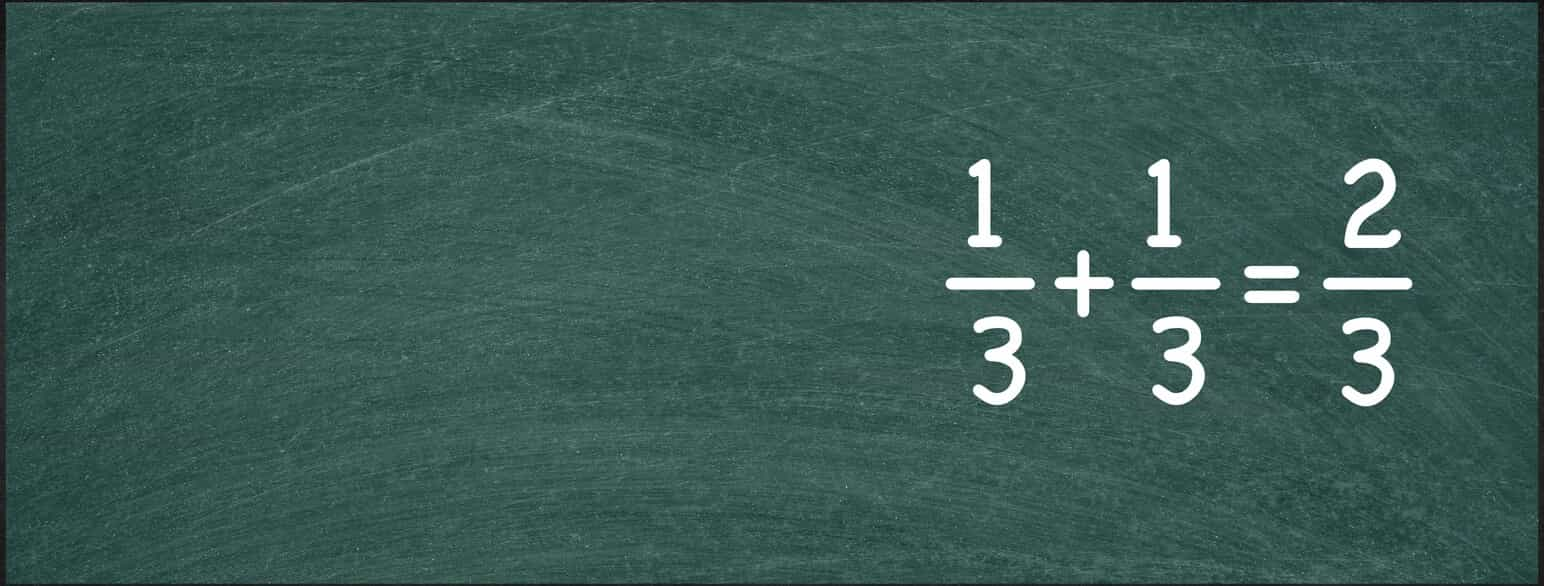Det er egne regler for addisjon, subtraksjon, multiplikasjon og divisjon med brøker.
Addisjon og subtraksjon: For å legge sammen to brøker, må de ha samme nevner. Da legger man sammen tellerne og beholder nevneren. For eksempel er \(\frac{1}{3}\) + \(\frac{1}{3}\) = \(\frac{2}{3}\).
Det samme gjelder også for subtraksjon. Hvis regnestykket er å trekke en brøk fra en annen, må nevnerne være like. Da trekker man den ene telleren fra den andre og beholder nevneren. For eksempel er \(\frac{3}{5}\) − \(\frac{1}{5}\) = \(\frac{2}{5}\).
Multiplikasjon: Når man skal gange sammen to brøker, så ganger man sammen tellerne og nevnerne hver for seg. Nevnerne trenger ikke være like. For eksempel er \(\frac{3}{4} \cdot \frac{2}{5}\) = \(\frac{6}{20}\).
Divisjon: Å dele en brøk med en annen kan virke litt komplisert. En huskeregel kan være at å dele på en brøk er det samme som å gange med den omvendte brøken. For eksempel er \(\frac{3}{4}\) delt på \(\frac{2}{5}\) det samme som å gange \(\frac{3}{4}\) med \(\frac{5}{2}\), altså er \(\frac{3}{4} : \frac{2}{5}\) = \(\frac{15}{8}\).
Hvis man ganger både teller og nevner med det samme tallet, endrer ikke brøken verdi. For eksempel er \(\frac{2}{5}\) det samme som \(\frac{4}{10}\) Her er både teller og nevner ganget med 2. Dette kalles å utvide brøken.
Man kan også dele teller og nevner med det samme tallet. For eksempel er \(\frac{8}{12}\) det samme som \(\frac{2}{3}\) . Her er både teller og nevner delt med 4. Dette kalles å forkorte brøken.