OGLE-2017-BLG-0329L: A Microlensing Binary Characterized with Dramatically Enhanced Precision Using Data from Space-based Observations

We first conduct an analysis of the event based on the data obtained from ground-based observations. We start modeling the light curve under the approximation that the relative lens-source motion is rectilinear ("standard model"). For this modeling, one needs seven principal lensing parameters. These parameters include the time of the closest source approach to a reference position of the binary lens, t₀, the lens-source separation at that time, u₀ (impact parameter), the event timescale, t_E, the projected separation s (normalized to θ_E), and the mass ratio q between the binary-lens components, the angle between the source trajectory and the binary-lens axis, α (source trajectory angle), and the normalized source radius ρ. We choose the barycenter of the binary lens as the reference position of the lens.

Since both the caustic crossings of the light curve were resolved, we consider finite-source effects. Finite-source magnifications are computed using the ray-shooting method (Kayser et al. 1986; Schneider & Weiss 1986; Wambsganss 1997). In computing lensing magnifications, we consider the surface-brightness variation of the source star caused by limb darkening. For this, we model the surface-brightness profile of the source star as $S\propto 1-{\rm{\Gamma }}(1-3\cos \phi /2)$, where Γ is the linear limb-darkening coefficient and ϕ is the angle between the line of sight toward the center of the source star and the normal to the surface of the source star. Based on the spectral type of the source star (see Section 4.1), we adopt Γ_I = 0.53.

To find the solution of the lensing parameters, we first conduct a grid search for the parameters $\mathrm{log}s$ and $\mathrm{log}q$, while the other parameters (t₀, u₀, t_E, ρ, α) at each point on the ($\mathrm{log}s,\mathrm{log}q$) plane are searched for by minimizing χ² using the Markov Chain Monte Carlo (MCMC) method. The ranges of the explored grid-parameter plane are $-1.0\leqslant \mathrm{log}s\leqslant 1.0$ and $-5.0\leqslant \mathrm{log}q\leqslant 1.0$. This first-round search yields local minima in the ($\mathrm{log}s,\mathrm{log}q$) plane. For each local minimum, we then refine the solution by allowing all parameters to vary. We identify a global minimum by comparing χ² values of the individual local solutions. From this modeling, we find a unique solution of the event. According to this solution, the event was produced by a binary with a mass ratio between the components of q ∼ 0.7 and a projected separation of s ∼ 1.4. Due to the similar masses of the binary components and the proximity of the separation to unity, the caustic forms a single big closed curve (resonant caustic).

Since the event can be subject to higher-order effects due to its long timescale, we conduct additional modeling considering two such effects. In the "parallax model" and "lens-orbital model," we separately consider the microlens-parallax and lens-orbital effects, respectively. We also conduct modeling by simultaneously considering both higher-order effects ("orbit+parallax model"). Consideration of the microlens-parallax effects requires us to include two additional parameters of π_E,N and π_E,E, which represent the north and east components of the microlens parallax vector ${{\boldsymbol{\pi }}}_{{\rm{E}}}$ projected on the sky in the north and east equatorial coordinates, respectively. Under the approximation that the positional change of the lens is small, the lens-orbital effects are described by two parameters ds/dt and dα/dt, which represent the change rates of the binary separation and the source trajectory angle, respectively. For parallax solutions, it is known that there can exist a pair of degenerate solutions with u₀ > 0 and u₀ < 0 due to the mirror symmetry of the lens system geometry (Smith et al. 2003; Skowron et al. 2011). We check this so-called "ecliptic degeneracy" whenever we consider microlens-parallax effects in modeling. The lensing parameters of the two solutions resulting from the ecliptic degeneracy are approximately in the relations of $({u}_{0},\alpha ,{\pi }_{{\rm{E}},N},d\alpha /{dt})\,\leftrightarrow$ $-({u}_{0},\alpha ,{\pi }_{{\rm{E}},N},d\alpha /{dt})$.

In Table 2, we present the goodness of the fits expressed in terms of χ² values for the individual tested models. From the comparison of χ² values, it is found that the model fit improves with the consideration of the higher-order effects. The improvement by the microlens-parallax and lens-orbital effects are χ² = 35.3 and 53.9, respectively. When both higher-order effects are simultaneously considered, on the other hand, it is found that the fit improvement is merely χ² = 7.4 with respect to the orbital model. From the fact that (1) the fit improvement by the lens-orbital effect is bigger than the improvement by the microlens-parallax effect and (2) the further improvement from the orbital model by additionally considering the microlens-parallax effect is small, we judge that the dominant higher-order effect is the lens-orbital effect and the microlens-parallax effect is relatively small.

The weakness of the microlens-parallax effect can also be seen in Figure 2, where we present the Δχ² distribution in the (π_E,N, π_E,E) plane obtained from the modeling considering both microlens-lens and lens-orbital effects. It shows that the model is consistent with the zero-π_E model by Δχ² ≲ 4. For the validation of the weak microlens-parallax interpretation, the lens parameters resulting from the orbit+parallax model should be physically permitted. For this, we estimate the ranges of the lens mass (M = M₁ + M₂) and the projected kinetic-to-potential energy ratio, which is computed by

$$\begin{eqnarray}&&{\left(\displaystyle \frac{\mathrm{KE}}{\mathrm{PE}}\right)}_{\perp }=\displaystyle \frac{{({a}_{\perp }/\mathrm{au})}^{3}}{8\pi (M/{M}_{\odot })}\left[{\left(\displaystyle \frac{1}{s}\displaystyle \frac{{ds}}{{dt}}\mathrm{year}\right)}^{2}+{\left(\displaystyle \frac{d\alpha }{{dt}}\mathrm{year}\right)}^{2}\right].\end{eqnarray} \tag{ 3 }$$

We describe the procedure to measure the angular Einstein radius θ_E, which is needed to determine M and ${(\mathrm{KE}/\mathrm{PE})}_{\perp }$, in Section 4.1. We find that the ranges of the lens mass and the energy ratio are 0.9 ≤ M/M_⊙ ≤ 4.6 and 0.04 ≤ (KE/PE)_⊥ ≤ 0.1, respectively. The estimated lens mass roughly corresponds to those of binaries composed of stars. The kinetic-to-potential energy ratio also meets the condition (KE/PE)_⊥ < KE/PE < 1, that is required for the binary lens to be a gravitationally bound system. Therefore, the solution based on the ground-based data is physically permitted, although the range of the estimated lens mass is very wide due to the large uncertainty of the measured π_E.

Zoom In Zoom Out Reset image size

Knowing the difficulty of the secure π_E measurement based on only the ground-based data, we test the possibility of π_E measurement with the additional data obtained from Spitzer observations. To compute lensing magnifications seen from the Spitzer telescope, one needs the position and the distance to the satellite. The position of the Spitzer telescope was in the ranges of 110° ≲ R.A. ≲ 194° and −7° ≲ decl. ≲ 21° and the distance was in the range of 1.566 ≲ d_sat/au ≲ 1.584 during the 2017 bulge season.

The Spitzer data partially covered the event light curve. Furthermore, they do not cover major features such as those produced by caustic crossings. See the Spitzer data presented in Figure 1. In such a case, external information of the color between the passbands used for observations from Earth and from the Spitzer telescope can be useful in finding a correct model (Yee et al. 2015; Shin et al. 2017). We, therefore, apply a color constraint with the measured instrumental color of I − L = 2.33 ± 0.012. The color constraint is imposed by giving penalty χ² defined in Equation (2) of Shin et al. (2017).

For single-lensing events observed both from Earth and from a satellite, it is known that there exist four sets of degenerate solutions (Refsdal 1966; Gould 1994b). This degeneracy among these solutions, referred to as (+, +), (−, −), (+, −), and (−, +) solutions, arises due to the ambiguity in the signs of the lens-source impact parameters as seen from Earth (the former sign in parenthesis) and from the satellite (the latter sign in parenthesis). In many cases of binary-lens events, this four-fold degeneracy reduces into a two-fold degeneracy (Han et al. 2017) due to the lack of lensing magnification symmetry. The remaining two degenerate solutions, (+, +) and (−, −) solutions, are caused by the mirror symmetry of the source trajectory with respect to the binary axis, and thus the degeneracy corresponds to the "ecliptic degeneracy." Besides the known types, binary events can be subject to various other types of degeneracy.

In order to check the existence of degenerate solutions, we explore the space of the lensing parameters using two methods. First, we conduct a grid search over the (π_E,N, π_E,E) plane. Second, we search for local solutions using a downhill approach from various starting points that are obtained from the analysis based on the ground-based data. From these searches, we identify two classes of solutions, in which each class is composed of two solutions arising from the ecliptic degeneracy.

In Figure 3, we present the locations of the local solutions in the (π_E,N, π_E,E) plane. It is found that one pair of solutions has ${\pi }_{{\rm{E}}}={({\pi }_{{\rm{E}},N}^{2}+{\pi }_{{\rm{E}},E})}^{1/2}\gtrsim 0.1$ ("big-π_E" solutions) and the other pair has π_E ≲ 0.1 ("small-π_E" solutions). For each pair, the lensing parameters of the two degenerate solutions are approximately in the relation of $({u}_{0},\alpha ,{\pi }_{{\rm{E}},N},d\alpha /{dt})\,\leftrightarrow -({u}_{0},\alpha ,{\pi }_{{\rm{E}},N},d\alpha /{dt})$, and thus we refer to the solutions as u₀ < 0 and u₀ > 0 solutions. We note that although the higher-order parameters (π_E,N, π_E,E, ds/dt, dα/dt) of these degenerate solutions are different from one another, the other lensing parameters are similar because they are mostly determined from the ground-based data. By comparing the ranges of the Δχ² distributions with and without the Spitzer data, one finds that the uncertainties of the determined microlens-parallax parameters are greatly reduced with the use of the Spitzer data.

Zoom In Zoom Out Reset image size

In Table 3, we list the lensing parameters of the four degenerate solutions along with their χ² values. We find that the (small-π_E)/(u₀ < 0) solution is preferred over the other solutions for two major reasons. First, the (small-π_E)/(u₀ < 0) solution provides a better fit to the observed data than the other solutions by 11.3 < Δχ² < 25.3. Second, the small-π_E solutions are preferred over the big-π_E solution according to the "Rich argument" (Calchi Novati et al. 2015a), which states that, other factors being equal, small parallax solutions are preferred over large ones by a probability factor (π_E,big/π_E,small)² ≳ 6. Although the (small-π_E)/(u₀ < 0) solution is favored, one cannot completely rule out the other degenerate solutions. We, therefore, discuss the methods that can firmly resolve the degeneracy in Section 5. Also presented in Table 3 are the fluxes of the source, f_S,I, and the blend, f_b,I, estimated based on the OGLE data. The small f_b,I indicates that the blend flux is small. We note that the small negative blending is quite common for point-spread-function photometry in crowded fields (Park et al. 2004).

In Figure 4, we present the lens-system geometry of the four degenerate solutions. For each geometry, we present the source trajectories with respect to the lens components (small empty dots marked by M₁ and M₂) and the caustic (cuspy closed curve). For each geometry, the source trajectories seen from Earth and the Spitzer telescope are marked by blue and red curves (with arrows), respectively. We also present the portion of the light curve in the vicinity of the Spitzer data and the model light curve.

Zoom In Zoom Out Reset image size

As mentioned, the degeneracy between the u₀ < 0 and u₀ > 0 solutions is caused by the mirror symmetry of the lens system geometry. On the other hand, the degeneracy between the small-π_E and big-π_E solutions is caused by the difference in the source trajectory angles seen from the Spitzer telescope. For the small-π_E solution, the source trajectory angle as seen from the Spitzer telescope is bigger than the angle of the source trajectory seen from the ground. In contrast, the Spitzer trajectory angle of the big-π_E solution is smaller than the angle of the ground trajectory. We note that the latter degeneracy is different from the degeneracy between (+, +) and (+, −) solutions because both ground and satellite trajectories pass on the same side with respect to the barycenter of the binary lens. Such a degeneracy is not previously known.

In order to further investigate the cause of the degeneracy between the small-π_E and big-π_E solutions, in Figure 5, we present the magnification contours in the outer region of the caustic. On the contour map, we plot the Spitzer source trajectories of the two degenerate solutions. From the map, it is found that the magnification patterns along the source trajectories of the two degenerate solutions are similar to each other, suggesting that the degeneracy is caused by the symmetry of the magnification pattern in the outer region of the caustic. We note that the degeneracy could have been resolved if the caustic exit part of the light curve had been covered by Spitzer data because the times of the caustic exit (seen from the Spitzer telescope) expected from the two degenerate solutions are different from each other. We find that the caustic exit times for the small-π_E solutions are in the range of 7926 (for u₀ < 0) ≲ HJD' ≲ 7928 (for u₀ > 0). On the other hand, the range for the big-π_E solutions is 7922 (for u₀ < 0) ≲HJD' ≲ 7924 (for u₀ > 0). With the ∼4 day time gap between the caustic-crossing times of the small-π_E and big-π_E solutions, the degeneracy could have been easily lifted. In conclusion, we find that the new type of degeneracy is caused by the partial symmetry of the magnification pattern outside the caustic combined with the fragmentary coverage of the Spitzer data.

Zoom In Zoom Out Reset image size

From the comparison of the analyses conducted with and without the space-based data, we find two important results.

• 1.  
  First, while the microlens parallax cannot be securely determined based on only the ground-based data, the addition of the Spitzer data enables us to clearly identify two classes of microlens-parallax solutions. The degeneracy is either intrinsic to lensing systems (u₀ < 0 versus u₀ > 0 degeneracy) or due to the combination of the partial symmetry of the magnification pattern combined with the fragmentary Spitzer coverage of the event (small-π_E versus big-π_E degeneracy).
• 2.  
  Second, the space-based data greatly improve the precision of the π_E measurement. We find that the measurement uncertainties of the north and east components of ${{\boldsymbol{\pi }}}_{{\rm{E}}}$ are reduced by factors of ∼18 and ∼4, respectively, with the use of the Spitzer data. Since the lens mass is directly proportional to 1/π_E, the uncertainty of the mass measurement reduces by the same factors.

For the unique determination of the lens mass and distance, one needs to estimate the angular Einstein radius in addition to the microlens parallax. Since the angular Einstein radius is determined by θ_E = θ_*/ρ, it is required to estimate the angular radius of the source star.

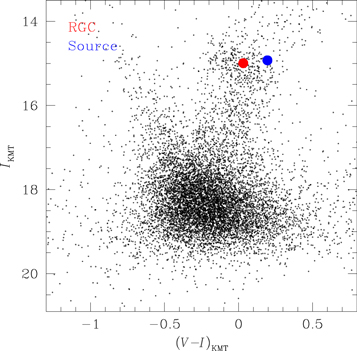
We estimate θ_* from the dereddened color (V − I)₀ and brightness I₀ of the source. In order to derive (V − I)₀ from the instrumental color–magnitude diagram, we use the method of Yoo et al. (2004), which uses the centroid of the red giant clump (RGC) as a reference. In Figure 6, we present the location of the source and the RGC centroid in the instrumental color–magnitude diagram constructed from the I- and V-band DoPHOT photometry of the KMTC data set. It is found that the offsets in color and brightness of the source with respect to the RGC centroid are Δ(V − I, I) = (0.16, −0.07). With the known dereddened color and magnitude of RGC centroid, (V − I, I)_RGC = (1.06, 14.5) (Bensby et al. 2011; Nataf et al. 2013), we find that the dereddened color and brightness of the source star are (V − I, I)₀ = (V − I, I)_RGC + Δ(V − I, I) = (1.22 ± 0.07, 14.48 ± 0.09). This indicates that the source is a K-type giant star. Using the color–color relation provided by Bessell & Brett (1988), we convert V − I into V − K. Using the relation between V − K and the surface brightness (Kervella et al. 2004), we estimate the angular source radius. The estimated angular source radius is θ_* = 6.9 ± 0.6 μas. Combined with the value of ρ, we estimate that the angular Einstein radius of the lens system is

$$\begin{eqnarray}&&{\theta }_{{\rm{E}}}=0.79\pm 0.06\ \mathrm{mas}.\end{eqnarray} \tag{ 4 }$$

With the measured angular Einstein radius, the relative lens-source proper motion is estimated by

$$\begin{eqnarray}&&\mu =6.89\pm 0.56\ \mathrm{mas}\ {\mathrm{yr}}^{-1}.\end{eqnarray} \tag{ 5 }$$

Zoom In Zoom Out Reset image size

With the measured microlens parallax and the angular Einstein radius, we estimate the mass and distance to the lens using the relations in Equation (2). For this, we estimate the distance to the source by ${D}_{{\rm{S}}}={D}_{\mathrm{GC}}(\cos l+\sin l\cos \phi /\sin \phi ),$ where D_GC = 8.16 kpc is the distance to the galactic center (Nataf et al. 2013), l = −254 is the galactic longitude of the source, and ϕ = 40° is the orientation angle of the bar-shaped bulge with respect to the line of sight. This results in D_S = 8.62 kpc and π_S = 0.116 mas. In Table 4, we list the determined physical parameters, including masses of the primary, M₁, and the companion, M₂, the distance to the lens, D_L, and the projected separation between the lens components, a_⊥ = sD_Lθ_E, for the individual degenerate lensing solutions. To check the physical validity of the parameters, we also present the ratio between the projected potential energy to the kinetic energy, i.e., (KE/PE)_⊥.

Due to the difference in the microlens-parallax values between the small-π_E and big-π_E solution classes, the estimated lens masses and distances for the two classes of solutions are substantially different from each other. On the other hand, the physical parameters for the pair of the u₀ > 0 and u₀ < 0 solutions are similar to each other. We find that the masses of the primary and companion are 1.1 ≲ M₁/M_⊙ ≲ 1.3 and 0.8 ≲ M₂/M_⊙ ≲ 0.9 for the small-π_E solutions. For the big-π_E solutions, the masses of the lens components are 0.4 ≲ M₁/M_⊙ ≲ 0.5 and M₂ ∼ 0.3 M_⊙. The estimated distances to the lens are 6.4 ≲ D_L/kpc ≲ 6.7 and 4.5 ≲ D_L/kpc ≲ 4.7 according to the small-π_E and big-π_E solutions, respectively.

The estimated masses of the lens for the small-π_E and big-π_E solutions are considerably different due to the difference in the measured microlens-parallax values. Then, if the lens-source can be resolved from future high-resolution imaging observations, the degeneracy can be resolved from the lens brightness.

If the proposed follow-up high-resolution observations are conducted, the observations will likely be conducted in the near-IR band. We, therefore, estimate the H-band magnitudes of the source and lens. From the dereddened I-band magnitude I₀ ∼ 14.5, the dereddened H-band source magnitude of the source is H₀ ∼ 13.1 (Bessell & Brett 1988). The V-band extinction of A_V ∼ 2.6 in combination with the extinction ratio (A_H/A_V) ∼ 0.108 (Nishiyama et al. 2008) toward the bulge field yields the H-band extinction of A_H ∼ 0.28. Then, the apparent H-band magnitude of the source is H_S = H₀ + A_H ∼ 13.4. We compute the lens brightness based on the mass and distance under the assumption that the lens and source experience the same amount of extinction. In Table 5, we present the expected combined (primary plus companion) I- and H-band magnitudes of the lens and source. The brightness of the lens varies depending on the solution. For the small-π_E solutions, the apparent H-band magnitude of the lens is H_L ∼ 16.5–17.0. For the big-π_E solutions, on the other hand, the expected H-band lens brightness is H_L ∼ 18.7–19.1.

According to the estimated I-band lens brightness, the lens-to-source flux ratio for the (small-π_E)/(u₀ > 0) solution is f_L,I/f_S,I ∼ 17%. Since the light from the lens contributes to blended light, then, this ratio is too big to be consistent with the small amount of the measured blended flux, even considering the uncertainties of the lens mass and distance. Therefore, the solution is unlikely to be the correct solution not only because of its worst χ² value among the degenerate solutions but also because of the limits on blended light. The lens-to-source flux ratio for the (small-π_E)/(u₀ < 0) is about 6%, but with the lens mass and distance at the 1σ (2σ) level, the ratio is ∼2% (1%), which is consistent with the blending.

The degeneracy between u₀ < 0 and u₀ > 0 solutions can also be lifted once the lens and source are resolved. The relative lens-source proper motion vector is related to t_E, θ_E, and (π_E,N, π_E,E) by

$$\begin{eqnarray}&&{\boldsymbol{\mu }}=({\mu }_{N},{\mu }_{E})=\left(\displaystyle \frac{{\theta }_{{\rm{E}}}}{{t}_{{\rm{E}}}}\displaystyle \frac{{\pi }_{{\rm{E}},N}}{{\pi }_{{\rm{E}}}},\displaystyle \frac{{\theta }_{{\rm{E}}}}{{t}_{{\rm{E}}}}\displaystyle \frac{{\pi }_{{\rm{E}},E}}{{\pi }_{{\rm{E}}}}\right).\end{eqnarray} \tag{ 6 }$$

For the pair of the degenerate solutions with u₀ < 0 and u₀ > 0, the north components of ${{\boldsymbol{\pi }}}_{{\rm{E}}}$ have opposite signs. This implies that the relative motion vectors of the two degenerate solutions are directed in substantially different directions and thus the degeneracy can be resolved from the lens motion with respect to the source.

The heliocentric lens-source proper motion is μ_helio ∼ 7 mas yr⁻¹, which is about what is expected for a disk lens. In this case, the expected direction of ${{\boldsymbol{\mu }}}_{\mathrm{helio}}$ (i.e., the direction of Galactic rotation ψ ∼ 30°) is roughly 30° east of north. In Table 4, we list the orientation angles ψ of ${{\boldsymbol{\mu }}}_{\mathrm{helio}}$, as measured from north to east, corresponding to the individual solutions. The heliocentric proper motion is related to the geocentric proper motion ${{\boldsymbol{\mu }}}_{\mathrm{geo}}$ by

$$\begin{eqnarray}&&{{\boldsymbol{\mu }}}_{\mathrm{helio}}={{\boldsymbol{\mu }}}_{\mathrm{geo}}+{{\boldsymbol{v}}}_{\oplus ,\perp }\displaystyle \frac{{\pi }_{\mathrm{rel}}}{\mathrm{au}},\end{eqnarray} \tag{ 7 }$$

where v_⊕,⊥ represents the projected Earth motion at t₀. One finds that the expected direction ${{\boldsymbol{\mu }}}_{\mathrm{helio}}$ is consistent with the (small-π_E)/(u₀ < 0) and the (big-π_E)/(u₀ > 0) solutions but inconsistent with the others.

From Keck adaptive optics observations, Batista et al. (2015) resolved the lens from the source ∼8.2 years after the event OGLE-2005-BLG-169, for which the relative lens-source proper motion is μ ∼ 7.4 mas yr⁻¹. The estimated proper motion of OGLE-2017-BLG-0329 (μ ∼ 6.9 mas yr⁻¹) is similar to that of OGLE-2005-BLG-169. Considering the large lens/source flux ratio, the lens-source resolution by Keck observations will take ∼10 years, which is somewhat longer than the time for OGLE-2005-BLG-169. We note that GMT/TMT/ELT, which will have better resolution than Keck, may be available before Keck can resolve the event and thus the time for follow-up observations can be shortened.