ABSTRACT
We present the results from deep X-ray observations (∼400 ks in total) of SN 1006 with Suzaku. The thermal spectrum from the entire supernova remnant (SNR) exhibits prominent emission lines of O, Ne, Mg, Si, S, Ar, Ca, and Fe. The observed abundance pattern in the ejecta components is in good agreement with that predicted by a standard model of Type Ia supernovae (SNe). The spatially resolved analysis reveals that the distribution of the O-burning and incomplete Si-burning products (Si, S, and Ar) is asymmetric, while that of the C-burning products (O, Ne, and Mg) is relatively uniform in the SNR interior. The peak position of the former is clearly shifted by 5' (∼3.2 pc at the distance of 2.2 kpc) to the southeast (SE) from the SNR's geometric center. Using the SNR age of ∼1000 yr, we constrain that the velocity asymmetry (in projection) of the ejecta is ∼3100 km s−1. The Fe abundance is also significantly higher in the SE region than in the northwest. Given that the non-uniformity is observed only in the heavier elements (Si through Fe), we argue that SN 1006 originates from an asymmetric explosion, as is expected from recent multidimensional simulations of Type Ia SNe, although we cannot eliminate the possibility that inhomogeneous ambient medium had induced the apparent non-uniformity. Possible evidence for the Cr-K-shell line and line broadening in the Fe-K-shell emission is also found.
1. INTRODUCTION
Despite many efforts in the last decades, explosion mechanism of Type Ia supernovae (SNe) is still unclear. It is widely known that Type Ia SNe show significant diversity in the optical spectra and the light curves (e.g., Phillips et al. 1999; Benetti et al. 2005). Theoretically, the diversity has been interpreted as a consequence of spherically asymmetric explosion (e.g., Kasen et al. 2009; but see also Mazzali et al. 2007). Maeda et al. (2010) systematically studied Type Ia SNe and attributed the observed spectral diversity to random viewing angles in almost identically symmetric explosions. In addition, multidimensional simulations have suggested that thermonuclear ignition in Type Ia progenitors is offset from the center (e.g., Woosley et al. 2004; Kuhlen et al. 2006; Röpke et al. 2007), which may result in a non-uniform distribution of the nucleosynthesis products.
Young supernova remnants (SNRs) in our Galaxy are ideal sites to investigate abundances and distribution of the SN ejecta in detail, since they are spatially well resolved, unlike extragalactic SNe. SN 1006, one of the prototypical Type Ia SNRs, is particularly important for such an investigation, owing to its proximity (2.2 kpc; Winkler et al. 2003) and moderate angular size (30' in diameter). It locates at a high Galactic latitude (b = 14.6), and hence has small foreground extinction. Therefore, it is a nice object to investigate the spatial information of low-Z elements, such as O, Ne, and Mg, of which K-shell emissions are observed in soft X-rays. Also its low and uniform ambient density (Dubner et al. 2002) enables us to study almost pure distribution of the ejecta with no significant modification due to the swept-up interstellar medium (ISM). Nonetheless, our knowledge of the ejecta has been limited because previous studies of SN 1006 have been mostly on the northeast (NE) and southwest (SW) rims, where the cosmic-ray acceleration (non-thermal X-ray) is dominant (e.g., Koyama et al. 1995; Bamba et al. 2003; Cassam-Chenaï et al. 2008).
Although Type Ia SNe yield a large amount of Fe (e.g., Iwamoto et al. 1999), detection of any signature of the Fe ejecta from SN 1006 has been hampered. One reason is that the thermal X-ray from the ejecta is faint compared with the bright non-thermal emission mainly from the cosmic-ray-accelerating rims. Furthermore, considerable fractions of the ejecta may not still be shocked to emit X-rays. In fact, blue- and redshifted absorption lines of Fe ii were detected in the UV spectra of the background stars, suggesting that unshocked Fe ejecta is freely expanding in the SNR's interior (Wu et al. 1993; Hamilton et al. 1997; Winkler et al. 2005). However, the inferred amount of cool Fe (<0.2 M☉) was much less than that of the theoretical prediction in the typical Type Ia SNe (∼0.7 M☉). Thus, a large amount of shocked Fe may be prevailing in the SNR. Possible evidence for the shocked Fe ejecta (i.e., X-ray line emission) in SN 1006 was firstly reported from the BeppoSAX observation (Vink et al. 2000). Yamaguchi et al. (2008) found more clear evidence for the Fe-K line at 6.43(± 0.02) keV using Suzaku. The mean ionization age of Fe corresponding to this centroid energy was found to be much lower than those of the other lighter elements (e.g., Si and S), suggesting that the Fe-rich core was heated by the reverse shock more recently.
Yamaguchi et al. (2008) also revealed that the Fe-K lines are brightest in the southeast (SE) quadrant, which may imply an asymmetric distribution of the Fe-rich ejecta. However, the detailed spectroscopy was limited within the SE region, and spatial distributions of the other lighter elements were not well investigated.
In this paper, we report a comprehensive study of the shocked ejecta in SN 1006 using the deep exposure (>400 ks) data of Suzaku. Thanks to the high sensitivity and good energy resolution, we are enabled to reveal detailed distribution of the ejecta. Throughout this paper, the distance to SN 1006 is assumed to be 2.2 kpc (Winkler et al. 2003), and errors quoted are at the 90% confidence level unless otherwise noted.
2. OBSERVATIONS AND DATA REDUCTION
We have performed several pointing observations of SN 1006 with the X-ray Imaging Spectrometer (XIS; Koyama et al. 2007) on board Suzaku (Mitsuda et al. 2007). The series of the observations covers almost the entire region of the SNR (Figure 1). The observations of the four quadrant regions were made during the performance verification (PV) phase by the Suzaku science working group. In order to compensate relatively low sensitivity near the edge of each field of view (FoV) and to study more about the ejecta in the SNR interior, we performed a deeper observation aiming at the SNR's center during the Announcement of Opportunity cycle 2 (AO2) phase. Detailed information of the observations is summarized in Table 1. We used XIS1 (back-illuminated CCD; BI CCD), and XIS0, 2, and 3 (front-illuminated CCDs; FI CCDs) for the PV-phase data, while for the AO2, XIS2 data were not available due to possible damage by a micrometeorite in 2006 November 9. We used the revision 2.4 of the cleaned event data and combined the 3 × 3 and 5 × 5 pixel events. The calibration database (CALDB) updated in 2011 September was used for the data reprocessing. We performed data reduction with the version 6.11 of the HEAsoft tools (ver. 18 of the Suzaku software).
Figure 1. Vignetting-corrected XIS image of SN 1006 in the 0.4–5.0 keV band. The FoVs of XISs are shown with the solid squares. The cross mark indicates the geometric center of SN 1006. The dashed line regions are bright non-thermal rims and a background point source (QSO 1504-4152; Winkler & Long 1997), which are excluded for the thermal spectrum analysis.
Download figure:
Standard image High-resolution imageTable 1. Observation Logs
| Name | ObsID | Obs. Date | (R.A., Decl.)J2000 | Exposure | |
|---|---|---|---|---|---|
| Source | NE | 100019020 | 2005 Sep 9 | (225.9608, −41.7805) | 22 ks |
| SW1 | 100019030 | 2005 Sep 10 | (225.5010, −42.0706) | 31 ks | |
| SW2 | 100019050 | 2006 Jan 26 | (225.4998, −42.0701) | 31 ks | |
| SE | 500016010 | 2006 Jan 30 | (225.8686, −42.0508) | 52 ks | |
| NW | 500017010 | 2006 Jan 31 | (225.6397, −41.7993) | 53 ks | |
| Center | 502046010 | 2008 Feb 25 | (225.7268, −41.9424) | 212 ks | |
| Background | NE_BGD | 100019010 | 2005 Sep 4 | (226.7036, −41.3998) | 45 ks |
| SW_BGD1 | 100019040 | 2005 Sep 11 | (224.6550, −42.4005) | 32 ks | |
| SW_BGD2 | 100019060 | 2006 Jan 26 | (224.6468, −42.4025) | 28 ks |
Download table as: ASCIITypeset image
3. ANALYSIS AND RESULTS
We employed xisrmfgen and xissimarfgen to generate the redistribution matrix files and ancillary response files, respectively (Ishisaki et al. 2007). For the following spectral analysis, we used the XSPEC software version 12.7.0 (Arnaud 1996). The data of the FI and BI CCDs were simultaneously analyzed, but only the FI spectra are shown throughout this paper for simplicity.
3.1. Galactic X-Ray Background
The combined XIS image of SN 1006 after subtraction of the non-X-ray background (NXB; xisnxbgen; Tawa et al. 2008) is shown in Figure 1. First, we divided the entire SNR into "non-thermal" and "thermal" regions and extracted spectra using all the five-pointing observations. The former consists of the NE and SW rims confined with the dotted lines in Figure 1, while the latter is the whole remaining region. We subtracted the cosmic X-ray background (CXB) from each spectrum by applying a power-law model with a photon index of 1.4 (Kushino et al. 2002).
The left panel of Figure 2 shows the NXB/CXB-subtracted spectra of the non-thermal and thermal regions. K-shell lines of O, Ne, Mg, Si, S, Ar, Ca, and Fe were clearly detected in the thermal spectrum. To see more detail around the Fe-K-shell line, we show the 5–10 keV band spectrum in the right panel of Figure 2. Besides the Fe-K line, we see line-like structure at ∼5.4 keV.
Figure 2. Left: FI spectra of the thermal and non-thermal regions in SN 1006, where the NXB and CXB are subtracted. The spectrum of the BGD region is also shown. Right: the magnified spectrum of the thermal region in 5.0–10.0 keV.
Download figure:
Standard image High-resolution imageWe obtained the Galactic X-ray background (BGD) data from near-sky three-pointing observations of SN 1006 (BGD; Table 1). The combined BGD spectrum after the subtraction of the NXB and CXB is shown in Figure 2. Although the BGD regions (and SN 1006) are located far off from the Galactic plane, we found clear excess X-rays. The excess X-rays were already found with the Tenma satellite (Koyama et al. 1987). Although its origin (thermal or non-thermal) was unclear, it was well described by a power-law model with a photon index of 2.1 ± 0.1. Ozaki et al. (1994) confirmed the excess X-rays with the Ginga satellite and represented the spectrum with a thermal bremsstrahlung model of 7 keV temperature. Soft X-rays from an evolved SNR, the Lupus Loop (Winkler et al. 1979), are widely spread over the full area of SN 1006, and hence would contaminate the soft X-ray band. In addition, possible contribution of the soft background (SB), which was often observed from off-plane sky regions such as the North Polar Spur (Miller et al. 2008) and the Milky Way halo (MWH) should not be ignored.
Since the observation dates of the SNR Center (AO2) and the BGD regions (PV phase) are largely separated, the difference in the energy resolution and event-detection efficiency among these observations cannot be ignored. We made, therefore, a model of the BGD spectrum, and added it to the source spectrum for the following fitting procedures, instead of the direct BGD subtraction.
As we noted, the BGD model should be composed of a power-law plus several thermal components with different electron temperatures. We fit the BGD spectrum with a model of these components. The best-fit results are shown in Figure 3 and Table 2. The photon index of the local excess was obtained to be 1.9 ± 0.1, consistent with the result of Koyama et al. (1987). We also found that the Lupus Loop has two temperature spectra with ∼0.22 keV and ∼0.98 keV.
Figure 3. Background spectrum fitted with several model components. The dash-dotted and dotted lines show emissions from SB and MWH, respectively. The spectra of the local excess and the Lupus Loop are fitted with a power-law and two thermal components, respectively (the solid lines).
Download figure:
Standard image High-resolution imageTable 2. Best-fit Parameters of the BGD Spectrum
| Component | NH | kTe | Γ | Fluxa |
|---|---|---|---|---|
| (× 1020 cm−2) | (keV) | (× 10−12 erg cm−2 s−1) | ||
| SB (CIE)b | ... | 0.1 (fixed) | ... | <0.55 |
| MWH (CIE)b | 5.6 (fixed) | 0.1 (fixed) | ... | 2.43 ± 0.21 |
| Local excess (power law) | 1.0 (fixed) | ... | 1.9 ± 0.1 | 1.68 ± 0.14 |
| The Lupus Loop1 (CIE)c | 1.0 (fixed) | 0.22 ± 0.01 | ... | 3.22 ± 0.14 |
| The Lupus Loop2 (CIE)c | 1.0 (fixed) | 0.98 ± 0.01 | ... | 1.28 ± 0.07 |
| χ2/dof | 439/355 = 1.24 |
Notes. aFlux in the 0.2–10.0 keV band. bAbundances were fixed to 1 solar. cAbundances were fixed to 0.2 solar.
Download table as: ASCIITypeset image
We then renormalized the flux of the BGD model by the effective area and added it to the source spectrum as the background components. We fixed all the BGD parameters determined in this way. To confirm the reliability of the background model, we fitted the spectrum of the non-thermal rims (NE and SW) with a power-law plus the BGD model, and obtained the best-fit photon index of ∼2.8. This value is consistent with a typical index of the synchrotron radiation in the X-ray band from the non-thermal rims of SN 1006 (e.g., Koyama et al. 1995).
3.2. Spectrum of the Entire Thermal Region
Yamaguchi et al. (2008) found that the Si and S-Kα lines in the spectrum of the SE region are significantly broadened compared with those expected from a single non-equilibrium ionization (NEI) plasma model. This broadening was interpreted as a superposition of multiple ejecta components with different ionization timescales. We found similar line broadening in the entire thermal spectrum, and hence applied two NEI plasma components with variable abundances (VNEI, NEIvers2.0+4; Borkowski et al. 2001) to represent high- and low-ionization ejecta of SN 1006 (hereafter Ejecta1 and Ejecta2, respectively). Free parameters were electron temperature kTe, ionization timescale net, emission measure EM = ∫nenHdV, and column density NH for interstellar absorption. Here, ne, nH, t, and V are the number densities of electrons and protons, elapsed time and the X-ray-emitting volume, respectively.
Since Type Ia SN ejecta should have a pure-metal composition with little contribution from H and He, we fixed the abundance of oxygen (Anders & Grevesse 1989) to be a sufficiently high value (1 × 104 solar), so that the bremsstrahlung from these elements is negligible compared with those originating from the heavy element ions. Abundances of C and N were fixed to 0, while those of Ne, Mg, Si, S, Ar, and Fe were allowed to vary freely, and that of Ni was linked to Fe. For Ejecta2, the Ca abundance was also linked to Fe, but that in Ejecta1 was a free parameter because L-shell lines of Ca may contribute to the spectrum in the soft X-ray band (<0.5 keV; see the Ejecta1 component in Figure 4).
Figure 4. FI spectrum of the thermal region fitted with the four-component model plus additional Gaussian lines: Ejecta1 (blue), Ejecta2 (light blue), ISM (light green), a non-thermal power law (orange), the magenta and red Gaussians for missing lines (see the text).
Download figure:
Standard image High-resolution imageSince the ionization timescale for Fe is very low (Yamaguchi et al. 2008), Ca would also emit K-shell lines from low-ionization states (Ejecta2). However, current NEI model does not include such emission lines. We therefore added a Gaussian line at 3.69 keV to represent the low-ionization Ca-K-shell line in Ejecta2. We further added an NEI model with the solar abundances and a power law to represent the swept-up ISM and the non-thermal emission, respectively. The energy band around the neutral Si-K edge (1.7–1.8 keV) was ignored, because the current response function is not accurate in this limited energy band.5 We also eliminated the 0.5–0.63 keV band, since the calibration of the contamination on the optical blocking filter was problematic.6
In this initial fit, we found a "shoulder"-shaped residual at around 0.7–0.8 keV. This feature was already noticed by Yamaguchi et al. (2008) and interpreted to be higher transition series of the O vii-K-shell lines (i.e., Kδ, K , etc., which are not incorporated in public NEI models). Since our NEI model also lacks the O vii-K-shell lines higher than Kδ, we added two Gaussians at 723 eV and 730 eV to represent K
, etc., which are not incorporated in public NEI models). Since our NEI model also lacks the O vii-K-shell lines higher than Kδ, we added two Gaussians at 723 eV and 730 eV to represent K and Kζ, respectively. The intensity ratio of Kζ/K
and Kζ, respectively. The intensity ratio of Kζ/K was assumed to be 0.5 (Yamaguchi et al. 2008) or 0.75 (Broersen et al. 2013). Although this fit was significantly improved (χ2/dof was reduced from 1300/839 to 1225/838) in the both cases, we need an unreasonably high intensity ratio of K
was assumed to be 0.5 (Yamaguchi et al. 2008) or 0.75 (Broersen et al. 2013). Although this fit was significantly improved (χ2/dof was reduced from 1300/839 to 1225/838) in the both cases, we need an unreasonably high intensity ratio of K and Kζ compared with those of lower-excitation level (e.g., K
and Kζ compared with those of lower-excitation level (e.g., K /Kδ ∼ 3.4). This may require a further additional line for the excess around 0.7 keV.
/Kδ ∼ 3.4). This may require a further additional line for the excess around 0.7 keV.
Usually, this energy band is dominated by the Fe xvii-L-shell emission of the 3s→2p transition with comparable flux to that of the 3d→2p transition at ∼0.8 keV (Foster et al. 2012). However, in an extremely low-ionized plasma, L-shell emissions from even lower charged Fe are also expected to occur following inner L-shell ionization. Although they can contribute to a spectrum around 0.7 keV, the current NEI code does not include any emission from these ions. In fact, our initial best-fit kTe ∼ 1.7 keV and net ∼ 1 × 109 cm−3 s (for Ejecta2) predict that the most dominant charge state of Fe is less than Fe16 +. Another young Type Ia SNR E0509−67.5, which also has an extremely low-ionization timescale of Fe (net < 2 × 109 cm−3; Kosenko et al. 2008), shows a similar excess around 0.7 keV (Warren & Hughes 2004). The weakness of the O vii and O viii emissions in SNR E0509−67.5 (Warren & Hughes 2004; Badenes et al. 2008), leads the excess to be mainly due to the Fe-L emission. Since the O vii-Kα line is strong in SN 1006 (see Figure 4 and Table 3), both the higher K-shell transitions of O vii and Fe-L emissions should be taken into account to the excess around 0.7 keV. For simplicity, we combined all the relevant lines (O vii-K , Kζ and Fe-L 3d→2p transitions) to a single Gaussian at around 0.7 keV. As we noted in the previous subsection, we found a line-like structure at ∼5.4 keV. We therefore added a Gaussian line in the final fitting. Then the center energy and flux were determined to be
, Kζ and Fe-L 3d→2p transitions) to a single Gaussian at around 0.7 keV. As we noted in the previous subsection, we found a line-like structure at ∼5.4 keV. We therefore added a Gaussian line in the final fitting. Then the center energy and flux were determined to be  keV and 3 ± 2 photons cm−2 s−1, respectively.
keV and 3 ± 2 photons cm−2 s−1, respectively.
Table 3. Best-fit Parameters (See Figure 4)
| Component | Parameter | Value | |
|---|---|---|---|
| Absorption | NH (× 1020 cm−2) | 6.80 ± 0.07 | |
| Ejecta1 (VNEI) | kTe (keV) | 0.48 ± 0.01 | |
| Abundance (104 solar) | C | 0 (fixed) | |
| N | 0 (fixed) | ||
| O | 1.0 (fixed) | ||
| Ne | 0.53 ± 0.02 | ||
| Mg | 3.71 ± 0.07 | ||
| Si | 13.7 ± 0.3 | ||
| S | 30 ± 1 | ||
| Ar | 27 ± 1 | ||
| Ca | 160 ± 8 | ||
| Fe | 0.56 ± 0.01 | ||
| Ni | (=Fe) | ||
| net (cm−3 s) | 4.39 ± 0.05 × 1010 | ||
| Fluxa (erg cm−2 s−1) | 7.85 ± 0.01 × 10−11 | ||
| Ejecta2 (VNEI) | kTe (keV) | 1.73 ± 0.03 | |
| Abundance (104 solar) | C | 0 (fixed) | |
| N | 0 (fixed) | ||
| O | 1.0 (fixed) | ||
| Ne | 0.53 ± 0.01 | ||
| Mg | 2.3 ± 0.1 | ||
| Si | 23.9 ± 0.4 | ||
| S | 25.2 ± 0.8 | ||
| Ar | 26 ± 3 | ||
| Ca | (=Fe) | ||
| Fe | 43 ± 3 | ||
| Ni | (=Fe) | ||
| net (cm−3 s) | 1.40 ± 0.01 × 109 | ||
| Fluxa (erg cm−2 s−1) | 8.66 ± 0.01 × 10−11 | ||
| ISM (NEI) | kTe (keV) | 0.4 ± 0.1 | |
| net (cm−3 s) |  |
||
| Fluxa (erg cm−2 s−1) | 4.60 ± 0.01 × 10−11 | ||
| Power law | Γ | 3.11 ± 0.02 | |
| Fluxa (photons cm−2 s−1) | 3.64 ± 0.03 × 10−2 | ||
| Emission line | Center energy (keV) | Normalization (photons cm−2 s−1) | 1σ width (eV) |
| Fe-L + O vii-K | 0.73 ± 0.01 | 3.92 ± 0.08 × 10−3 | 0 (fixed) |
| Ca-K | 3.69 (fixed) | 1.8 ± 0.4 × 10−5 | 0 (fixed) |
| Cr-K |  |
3 ± 2 × 10−6 | 0 (fixed) |
| Fe-K | 6.45 ± 0.02 | 2.6 ± 0.4 × 10−5 |  |
| χ2/dof | 1225/838 = 1.46 | ||
Note. aFlux in the 0.2–10.0 keV band.
Download table as: ASCIITypeset image
The best-fit results of this final model are given in Figure 4 and Table 3. The results are basically the same as those of Yamaguchi et al. (2008); the spectrum consists of a power law, and plasmas of ISM and two ejecta components with the different ionization timescales, the abundances of the both ejecta components are consistent with each other for Ne through Ar within a factor of ∼2, whereas the Fe abundance in Ejecta2 is more than one order of magnitude larger than that in Ejecta1.
In Figure 4, we see excess structures at the both sides of the line at ∼6.4 keV. This feature is likely due to broadening of the Fe-Kα line. We therefore fit the line with a Gaussian model and found the line energy and width to be 6.45 ± 0.02 keV and  eV, respectively (Table 3). Although Ejecta1 has an extremely large abundance of Ca (Table 3), this value should not be taken seriously, because the Ca abundance is mainly determined by the L-shell lines, in which uncertainty in the atomic data is large.
eV, respectively (Table 3). Although Ejecta1 has an extremely large abundance of Ca (Table 3), this value should not be taken seriously, because the Ca abundance is mainly determined by the L-shell lines, in which uncertainty in the atomic data is large.
We found that the contribution of the ISM component is relatively lower than the result of SE (Figure 8 in Yamaguchi et al. 2008), but is consistent with the interpretation by Cassam-Chenaï et al. (2008); the O emission in the entire SNR predominantly originates from the shock heated ejecta rather than the ISM.
3.3. Spatially Resolved Analysis
Figure 5 shows the vignetting-corrected narrowband images of the Kα lines from O, Ne, Mg, Si, and S after subtraction of the underlying continuum levels estimated by the interpolation of the adjacent band fluxes. The images show rim-brightening morphology, particularly in the light elements such as O, Ne, and Mg. In the interior regions, O, Ne, and Mg are rather uniformly distributed. In contrast, the distributions of Si and S are more asymmetric in the inner region; the SE rim is much brighter than the other regions, and the "second shell" can be seen at the middle between the outermost shell and the SNR's center. We also present the ratio maps of Si/O, S/O, Si/Ne, and Si/Mg in Figure 6. All the ratios show clear increases toward the SE rim, suggesting asymmetric ejecta distribution for the heavier elements (i.e., Si and S).
Figure 5. Vignetting-corrected intensity maps of the Kα lines from O, Mg, and Si. The geometric center of SN 1006 is indicated with the cross marks.
Download figure:
Standard image High-resolution imageFigure 6. Images the line flux ratio of the Kα lines of Si to O, S to O, Si to Ne, and Si to Mg. The geometric center of SN 1006 is shown with the cross marks. The spectral extraction regions are shown with the thin white lines. The width of each annular is 2'. The thick white lines divide the remnant into three parts named respectively, as S (southeast), C (center), and N (northwest).
Download figure:
Standard image High-resolution imageTo investigate more quantitatively, we divided the entire SNR into three regions: a center circle of the 8'radius (C), and half-annuluses of northwest (N) and southeast (S) (the thick white lines in Figure 6). The geometric center of the remnant was defined to be (α, δ)J2000.0 = (225.7371, −41.9336). The spectra of these three regions are shown in Figure 7. We fitted the spectra with the same four-component model (and the same assumptions) applied for the entire thermal spectrum. The best-fit results are given in Table 4. We found that the heavier elements are indeed more abundant in the region S than in the region N.
Figure 7. FI spectrum of SN 1006 obtained from the regions S, C, and N. Each spectrum was fitted with the same four-component model as the whole region.
Download figure:
Standard image High-resolution imageTable 4. Best-fit Parameters (See Figure 7)
| Component | Parameter | Value | |||
|---|---|---|---|---|---|
| Region S | Region C | Region N | |||
| Absorption | NH (× 1020 cm−2) | 6.8 ± 0.1 | 6.8 ± 0.1 | 6.8 ± 0.2 | |
| Ejecta1 (VNEI) | kTe (keV) | 0.95 ± 0.01 | 0.95 ± 0.01 |  |
|
| Abundance (104 solar) | C | 0 (fixed) | 0 (fixed) | 0 (fixed) | |
| N | 0 (fixed) | 0 (fixed) | 0 (fixed) | ||
| O | 1.0 (fixed) | 1.0 (fixed) | 1.0 (fixed) | ||
| Ne | 0.45 ± 0.03 | 0.54 ± 0.02 | 0.45 ± 0.07 | ||
| Mg | 3.0 ± 0.1 | 2.17 ± 0.05 | 2.4 ± 0.2 | ||
| Si | 6.8 ± 0.2 | 6.7 ± 0.2 | 2.7 ± 0.4 | ||
| S | 7.3 ± 0.8 | 8.8 ± 0.7 | <2 | ||
| Ar | 28 ± 2 | 14 ± 1 | 35 ± 5 | ||
| Ca | 28 ± 2 | 34 ± 12 | 110 ± 50 | ||
| Fe | 0.65 ± 0.02 | 0.40 ± 0.01 | 0.46 ± 0.05 | ||
| Ni | (=Fe) | (=Fe) | (=Fe) | ||
| net (cm−3 s) | 2.66 ± 0.09 × 1010 | 1.91 ± 0.05 × 1010 | 1.8 ± 0.2 × 1010 | ||
| Fluxa (erg cm−2 s−1) | 1.02 ± 0.01 × 10−11 | 1.73 ± 0.01 × 10−11 | 0.32 ± 0.01 × 10−11 | ||
| Ejecta2 (VNEI) | kTe (keV) |  |
2.50 ± 0.09 |  |
|
| Abundance (104 solar) | C | 0 (fixed) | 0 (fixed) | 0 (fixed) | |
| N | 0 (fixed) | 0 (fixed) | 0 (fixed) | ||
| O | 1.0 (fixed) | 1.0 (fixed) | 1.0 (fixed) | ||
| Ne | <0.02 | 0.41 ± 0.06 | 0.58 ± 0.03 | ||
| Mg | 2.1 ± 0.2 | 3.3 ± 0.6 | 2.5 ± 0.2 | ||
| Si | 24 ± 1 | 37 ± 2 | 12.9 ± 0.7 | ||
| S | 30 ± 2 | 34 ± 3 | 10 ± 1 | ||
| Ar | 14 ± 7 | 32 ± 10 | <5 | ||
| Ca | (=Fe) | (=Fe) | (=Fe) | ||
| Fe | 20 ± 5 | 17 ± 5 | 3 ± 2 | ||
| Ni | (=Fe) | (=Fe) | (=Fe) | ||
| net (cm−3 s) | 1.58 ± 0.02 × 109 | 1.31 ± 0.04 × 109 | 1.41 ± 0.02 × 109 | ||
| Fluxa (erg cm−2 s−1) | 2.08 ± 0.04 × 10−11 | 1.29 ± 0.01 × 10−11 | 1.47 ± 0.01 × 10−11 | ||
| ISM (NEI) | kTe (keV) | 0.4 (fixed) | 0.4 (fixed) | 0.4 (fixed) | |
| net (cm−3 s) | 5.1 × 109 (fixed) | 5.1 × 109 (fixed) | 5.1 × 109 (fixed) | ||
| Fluxa (erg cm−2 s−1) | 2.22 ± 0.01 × 10−11 | 1.76 ± 0.01 × 10−11 | 0.91 ± 0.01 × 10−11 | ||
| Power law | Γ | 2.98 ± 0.03 | 3.16 ± 0.04 | 3.27 ± 0.03 | |
| Fluxa (photons cm−2 s−1) | 0.68 ± 0.01 × 10−2 | 0.64 ± 0.01 × 10−2 | 0.63 ± 0.01 × 10−2 | ||
| χ2/dof | 670/604 = 1.11 | 751/569 = 1.32 | 560/511 = 1.10 | ||
Note. aFlux calculated 0.2–10.0 keV.
Download table as: ASCIITypeset image
We further divided the whole SNR into 16 regions: eight annuli with the width of 2' and each divided into half-rings of the northwest (NW) and SE part (solid lines in Figure 6). Then we fitted each spectra with the same four-component model. Since the statistics of the Fe line was insufficient, we fixed its abundance to the best-fit value in Table 4. The best-fit EMs for each element in the ejecta (Electa1+ Ejecta2) are given in Figure 8.
Figure 8. Radial profiles of the emission measure (EM) for various elements (O, Mg, Si, S, Ar, and Fe) in the ejecta. Red, blue, and black represent the results of Ejecta1, Ejecta2 (see Table 3), and summation of them, respectively. Note that the vertical scales of the EM of Mg and Ar (EMMg, Ar) are 1/5 of those of O, Si, S, and Fe (EMO, Si, S, Fe). The horizontal axis shows the distance from the geometric center of SN 1006; the positive and negative values are the NW and SE sides, respectively.
Download figure:
Standard image High-resolution image4. DISCUSSION
4.1. Elemental Abundances in the Ejecta
In Section 3.2, we successfully modeled the spectrum of the entire thermal region with the components applied previously by Yamaguchi et al. (2008). The emission lines of the heavy elements exhibit clear evidence for overabundance relative to the solar values, indicating the SN ejecta origin. The difference in the ionization age between the two components suggests that Ejecta2 was heated more recently than Ejecta1. The suppressed relative abundance of Fe in Ejecta1 (Table 3) implies absence of Fe in the outer ejecta layer, consistent to the previous claim by Yamaguchi et al. (2008).
We find a possible line feature at ∼5.4 keV. This centroid energy suggests its origin to be Cr-Kα emission. To examine this possibility, we plot in Figure 9 the Cr-Kα and Fe-Kα centroids observed in other SNRs (e.g., Yang et al. 2013) and compare with our results. We find the values from SN 1006 are reasonably close to the Cr-Kα–Fe-Kα centroid correlation, supporting our claim of the first detection of Cr from this remnant.
Figure 9. K-shell line energy of Fe vs. that of Cr in SN 1006. We also plotted previous results of W49B (Hwang et al. 2000), Tycho (Tamagawa et al. 2009), G344.7-0.1 (Yamaguchi et al. 2012), and other remnants (Yang et al. 2013) with circles. Open squares at lower left and upper right represent the values for the neutral and He-like states, respectively.
Download figure:
Standard image High-resolution imageSince atomic data for Cr are not available in the current NEI model, we estimate the emissivity εCr following the method of the ASCA measurement for W49B (Hwang et al. 2000). Using the best-fit temperature and the ionization timescale for the Ejecta2 component, we calculate emissivities for Si, S, Ar, and Fe. The results are given in Figure 10. Interpolating these values to that of Cr, we estimated the Cr/Fe abundance ratio ZCr/ZFe to be 2.5 ± 1.9 solar. Here, we assumed that Cr is mainly contained in Ejecta2 as the case of Fe.
Figure 10. Emissivity of heavy elements relative to that of Fe. These values were calculated from the NEI model of the best-fit Ejecta2 temperature and ionization parameter. The line is a spline fit to them.
Download figure:
Standard image High-resolution imageAs we noted, the NEI model we used also lacks emission data of Ca in the low-ionization state (Ejecta2). Therefore, we estimated ZCa/ZFe with the same method to be 0.8 ± 0.2 in Ejecta2. This result is consistent with our initial assumption that the abundance of Ca is nearly equal to Fe in Ejecta2.
We compare the abundances of Ejecta2 (relative to O) with the nucleosynthesis yields predicted by several theoretical models (Figure 11). We employ the Type Ia deflagration or delayed-detonation models (Iwamoto et al. 1999) and the core-collapse SN models with various progenitor masses (15 M☉, 20 M☉, 30 M☉, and 40 M☉; Woosley & Weaver 1995) The observed abundance pattern is confirmed to be broadly consistent with the standard Type Ia models. The abundance ratios of Si/O, S/O, Ar/O, and Ca/O are enhanced compared with those predicted by the W7 deflagration model, and slightly closer to the yields of the delayed-detonation explosion (CDD1).
Figure 11. Metal abundances of Ejecta2 relative to O as a function of atomic number (the solid line and "×" marks). The dashed lines and circles represent the delayed detonation, i.e., CDD1 (one of the DDT models), and classical deflagration model, W7 (Iwamoto et al. 1999). The dotted lines and triangles represent core-collapse models with main-sequence masses of 15 M☉, 20 M☉, 30 M☉, and 40 M☉, respectively (Woosley & Weaver 1995).
Download figure:
Standard image High-resolution image4.2. Three-dimensional Geometry of SN 1006
The spherical outer shell with the rim brightening in O, Ne, and Mg (Figure 5) would be mainly due to the ISM components, because the ejecta distributions in Figure 8 show no enhancement in these regions. On the other hand, the interior is likely to be dominated by the ejecta (see, e.g., Figure 8). Then the ejecta distributions are broadly separated into two patterns: the uniform interior for the lighter elements (O, Ne, and Mg) and more asymmetric distribution of the heavier elements (Si and S) with offset peak positions by 5' (∼3.2 pc). The off-center distribution of the heavier elements is also confirmed in Figure 6. Notably, these two groups (O–Ne–Mg and Si–S) are synthesized in different nuclear burning processes in Type Ia SN explosion: C burning for O–Ne–Mg, whereas O burning and incomplete Si burning for Si–S. We thus presume that the latter products distribute more asymmetrically than the former.
The asymmetry of the ejecta should be formed either at the time of the SN explosion or in the process of the following interaction with the ISM. If an ambient density in the SE is higher than those in the other regions, a reverse shock might heat up the ejecta earlier, which may explain the relative enhancement of the EM in the SE. In order to estimate the ambient densities in the SE and the NW rims, we made spectra from an annulus at the outer edges of the SE and NW. We fitted the spectra and found the best-fit normalizations (EM) of the ISM components 2.46 ± 0.29 × 10−4 cm−5 and 1.93 ± 0.22 × 10−4 cm−5 for the SE and NW, respectively. Given that SN 1006 is a sphere with a radius of 10.2 pc, the volume of the annulus is estimated to be 35 pc3. Then the ISM densities are nH = 0.11 ± 0.01 cm−3 and 0.09 ± 0.01 cm−3, hence the ambient densities (nH/4) are ∼0.03 cm−3 and ∼0.02 cm−3, for SE and NW, respectively. Previous observations (e.g., Heng et al. 2007) indicate that the ambient density in the NW is 0.15–0.3 cm−3, significantly higher than our result. Since the best-fit normalization (EM) was coupled with that of net and anti-correlated to kTe, a higher value of nH/4 (up to ∼0.1 cm−3) is statistically acceptable in the NW. The annulus we used for the spectrum is broader than the outermost edge of the recent shock encounter. On the other hand, the forward shock in the NW interacted with the denser region fairly recently (Katsuda et al. 2013), which may explain the discrepancy between our result and the previous studies.
Accordingly, within possible statistical and systematic uncertainty, we can conclude that the ambient density in the SE is lower than 0.1 cm−3 and does not particularly exceed those in the other rims. Furthermore, if an inhomogeneous ambient density has affected the large-scale variation of the ejecta, the lighter elements (O, Ne, and Mg) should similarly distribute asymmetrically. As shown in Figure 6, the actual distributions clearly refute this hypothesis. Thus, it is more plausible that the ejecta asymmetry was made by an asymmetric SN explosion.
We found the "second shell" in Si and S at the middle between the outermost shell and the SNR's center (∼6' from the center). The "second shell" is most likely from the ejecta, because we see a peak of Si and S at this position in the ejecta abundance (Figure 5). Since the foreground absorption is negligible in the energies above ∼1.5 keV, this second-shell structure is not due to absorption effect, but is likely to originate from the ejecta rim, reminiscent of similar double-shell morphology in G299.2-2.9 (Park et al. 2007; although this remnant is dominated by swept-up ISM, unlike SN 1006).
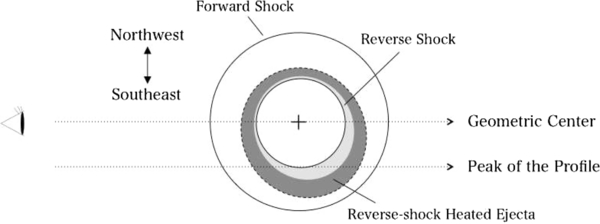
We also found that the EM of Fe increases from the NW to SE, as Yamaguchi et al. (2008) presumed that the Fe-rich core spreads out to SE. These results indicate that the ejecta, particularly heavier elements in more inner region, expand preferentially toward the SE. Based on the broad UV absorption lines of Si and Fe of several background objects, Hamilton et al. (1997) estimated that the diameter toward the far side of SN 1006 is roughly 20% larger than that of the rest of the remnant (see Figure 7 of Hamilton et al. 1997). Winkler et al. (2005) also confirmed the ejecta structure of Si and Fe by the similar analysis that the shell of SN 1006 is almost spherical (see Figure 8 of Winkler et al. 2005). We thus propose that the ejecta expanded not only transverse to but also along the line of sight; the ejecta were displaced toward the SE and far side of the center (Figure 12). If the reverse shock heated up a part of the ejecta components, then the centrally peaked profile is easy understood (Figure 12). Also, if the reverse shock recently reached the surface of the Fe-rich core (light-gray region in Figure 12), the EM should be higher at the shifted direction (lower right in Figure 12).
Figure 12. Schematic diagram of the ejecta structure of SN 1006. The gray area represents the ejecta already heated by the reverse shock. The light-gray and dark-gray regions correspond to the Fe-rich core and the Si-rich layer, respectively. The heavy elements are displaced to the far side and the SE (see the text).
Download figure:
Standard image High-resolution imageIncluding the "second shell," the peak positions of the heavy elements (Si, S, and Ar) are ∼5' = 3.2 pc away from the geometric center to SE (Figure 8). Assuming the distance of 2.2 kpc and the SNR age of 1000 yr, we estimate that the velocity difference (asymmetric explosion) between the SE and NW directions is ∼3100 km s−1 in projection. We found that Fe-Kα is broadened by  eV (1σ), for the first time from SN 1006. If this width is due to the Doppler broadening of the ejecta as is the case of Tycho (Hayato et al. 2010), the expansion velocity in the line of sight should be ∼3000 km s−1. This value is consistent with those by Katsuda et al. (2013) in which they measured the proper motion of the NW rim in X-ray.
eV (1σ), for the first time from SN 1006. If this width is due to the Doppler broadening of the ejecta as is the case of Tycho (Hayato et al. 2010), the expansion velocity in the line of sight should be ∼3000 km s−1. This value is consistent with those by Katsuda et al. (2013) in which they measured the proper motion of the NW rim in X-ray.
5. SUMMARY
This paper focused on the thermal spectrum of SN 1006 based on the deep observation (∼400 ks in total) with Suzaku XIS. The results are summarized as follows.
- 1.The X-ray spectra are well represented by a model with three NEI thermal plasmas (ejecta with different ionization parameters and ISM) plus one power-law component (non-thermal emission).
- 2.The ejecta abundance ratios of Ne, Mg, Si, S, Ar, Ca, Cr, and Fe relative to O are all in good agreement with yields predicted by the standard Type Ia theories: the classical carbon-deflagration model and the deflagration to detonation transition mechanism.
- 3.The distribution of the centroids of Si, S, and Ar is significantly shifted from the SNR's geometric center by ∼3.2 pc toward the SE, which we argue is likely to be associated with an asymmetric explosion of the progenitor. The velocity (in projection) difference of the ejecta is ∼3100 km s−1 at the distance of 2.2 kpc. The morphology of O, Ne, and Mg in the interior is more symmetric.
- 4.We found possible evidence for the Cr-K-shell line and line broadening in the Fe-K-shell emission.
The authors thank Dr. T. G. Tsuru and Dr. M. Nobukawa for carefully reading our manuscript. H.U. is supported by Japan Society for the Promotion of Science (JSPS) Research Fellowship for Young Scientists. K.K. is supported by JSPS KAKENHI grant Nos. 23000004 and 24540229. This work was supported by the Grant-in-Aid for the Global COE Program "The Next Generation of Physics, Spun from Universality and Emergence" from the Ministry of Education, Culture, Sports, Science and Technology (MEXT) of Japan.
Facility: Suzaku (XIS) - Suzaku (ASTRO-EII)
Footnotes
- 4
NEI based on improved atomic data including inner shell processes. See also Badenes et al. (2006) for more detail.
- 5
- 6