Abstract
KV Vel is a noneclipsing short-period (P = 0.3571 days) close binary containing a very hot subdwarf primary (77,000 K) and a cool low-mass secondary star (3400 K) that is located at the center of the planetary nebula DS 1. The changes in the orbital period of the close binary were analyzed based on 262 new times of light maximum together with those compiled from the literature. It is discovered that the O − C curve shows a small-amplitude (0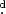 0034) cyclic period variation with a period of 29.55 yr. The explanation by the solar-type magnetic activity cycles of the cool component is ruled out because the required energies are much larger than the total radiant energy of this component in a whole cycle. Therefore, the cyclic variation was plausibly explained as the light-travel time effect via the presence of a tertiary component, which is supported by the periodic changes of the O − C curve and the rather symmetric and stable light curves obtained by the Transiting Exoplanet Survey Satellite. The mass of the tertiary companion is determined to be
0034) cyclic period variation with a period of 29.55 yr. The explanation by the solar-type magnetic activity cycles of the cool component is ruled out because the required energies are much larger than the total radiant energy of this component in a whole cycle. Therefore, the cyclic variation was plausibly explained as the light-travel time effect via the presence of a tertiary component, which is supported by the periodic changes of the O − C curve and the rather symmetric and stable light curves obtained by the Transiting Exoplanet Survey Satellite. The mass of the tertiary companion is determined to be  M⊙. If the third body is coplanar with the central binary (i.e.,
M⊙. If the third body is coplanar with the central binary (i.e.,  ), the mass of the tertiary component is computed as M3 ∼ 0.068 M⊙, and thus it would be below the stable hydrogen-burning limit and is a brown dwarf. The orbital separation is shorter than 9.35 au. KV Vel together with its surrounding planetary nebula and the brown-dwarf companion may be formed through the common-envelope evolution after the primary filled its Roche lobe during the early asymptotic giant branch stage.
), the mass of the tertiary component is computed as M3 ∼ 0.068 M⊙, and thus it would be below the stable hydrogen-burning limit and is a brown dwarf. The orbital separation is shorter than 9.35 au. KV Vel together with its surrounding planetary nebula and the brown-dwarf companion may be formed through the common-envelope evolution after the primary filled its Roche lobe during the early asymptotic giant branch stage.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
About one in five planetary nebulae (PNe) are formed from the evolutions of common envelopes (e.g., Miszalski et al. 2009). The central stars of these PNe are usually close binaries with a very hot subdwarf star and a very cool secondary star in detached configurations. Therefore, they usually show very strong reflection effects with amplitudes exceeding one magnitude and emission-line-dominated spectra (e.g., Shimansky et al. 2006). Most of them are likely evolving from the asymptotic giant branch (AGB; e.g., Iben & Tutukov 1993). The embedded PNe in these binary systems suggest that they are very young from the common envelope evolution. They are important targets for investigating the evolution of common envelopes and are the progenitors of cataclysmic variables. Some exoplanets or brown dwarfs have been found to be orbiting around subdwarf and white-dwarf binaries (e.g., Qian et al. 2009, 2012, 2013; Beuermann et al. 2012; Han et al. 2018; Zhu et al. 2019; Sale et al. 2020; Chiodo et al. 2022). Among them, V471 Tau (DAZ+K2V; P = 12.52 hr) is very special for understanding fundamental aspects of stellar astrophysics and binary evolution (Chiodo et al. 2022), which is a member of the Hyades cluster, and a brown-dwarf companion is detected (e.g., Chiodo et al. 2022; Kundra et al. 2022). However, no substellar objects companions to the central binaries of PNe have been reported to date.
KV Vel was originally discovered as an sdO star that possesses a PN DS 1 (Drilling 1983; Holmberg et al. 1978). The nebula is roughly circular with a diameter of ∼180''. Later, radial-velocity curves for both binary components were measured by Drilling (1985) with an orbital period of 8.57 hr, indicating that it is the first PNe central star discovered to be a double-lined spectroscopic binary. The binary system consists of a hot subdwarf and a cool M dwarf with a temperature difference of up to 73,600 K (Hilditch et al. 1996; Ribeiro & Baptista 2011). Photometric light curves have been published by Drilling (1985), Landolt & Drilling (1986), Kilkenny et al. (1988), and Ribeiro & Baptista (2011), which show a very strong reflection effect of the secondary star with an amplitude of ΔV ∼ 0.55 mag in V (Hilditch et al. 1996) and ΔH ∼ 0.7 at near-infrared wavelengths. It is one of the most pronounced such effects observed to date. The symmetric shape of the reflection effect with respect to the phase of maximum indicates that it is produced by uniform irradiation of the cool component by a source centered on the position of the extremely hot subdwarf primary. The very large amplitude and the symmetric shape of the reflection effect indicate that the times of maximum can be determined with high precision. Therefore, the changes in the orbital period could be investigated in detail.
2. Variations in the Orbital Period Change
The orbital period of KV Vel, the central binary star surrounded by a PN DS 1 (Drilling 1983; Holmberg et al. 1978), was first determined as 8.571 hr by Drilling (1985). Based on multicolor photometry observations, Landolt & Drilling (1986) gave the first photometric ephemeris,

This ephemeris was later improved by Kilkenny et al. (1988) by using Drilling data and their own data as

Near-infrared light curves in JHK bands were obtained by Ribeiro & Baptista (2011). They determined one time of maximum light and found that the maximum time is displaced by 0.01 phases from the ephemeris of Kilkenny et al. (1988), which cannot be accounted for by the uncertainty. Therefore, a revised photometric ephemeris,

was derived by Ribeiro & Baptista (2011) by adding the near-infrared time of maximum.
Long-term photometric observations are very important to investigate the change in the orbital period of close binary stars. The Digital Access to a Sky Century at Harvard project (DASCH) is committed to digitizing the glass photographic plates that have accumulated for more than 100 yr, and providing photometric data available online (Grindlay et al. 2009, 2012). As for KV Vel, there are 1567 DASCH observations in the time interval between HJD 2414077 and HJD 2447708. In total, 21 times of light maximum were determined from the DASCH data by using a method similar to the semi-automatic fitting procedure method (Zasche et al. 2014), which was also demonstrated and adopted by us (e.g., Liu et al. 2015; Li et al. 2023). By using the same method, several times were also computed by using the ASAS-SN database (Shappee et al. 2014; Jayasinghe et al. 2019). Two of the examples are shown in the upper panels of Figure 1, where one time of light maximum in the left panel was determined from DASCH in the time interval between HJD 2416000 and 2419500, while the other one derived from the ASAS-SN data is displayed in the right panel. The uncertainties associated with the times of light maximum in the light curve were determined through the calculation of the covariance. Moreover, KV Vel was observed by the Transiting Exoplanet Survey Satellite (TESS; Ricker et al. 2015) in four sectors from 2019 April to 2023 March, i.e., S10, S36, S37, and S63. A part of the TESS light curves is plotted in the lower panel of Figure 1. As shown in the panel, the TESS light curve is symmetric and rather stable. A large number of times of maximum light were obtained with TESS data. In total, 262 new times of light maximum have been determined and the time span of our data is more than 120 yr (HJD 2416120–260040.5), which is very useful for analyzing the long-term changes in the orbital period of KV Vel.
Figure 1. Upper panels: maxima of KV Vel from DASCH (left panel) and ASAS-SN (right panel). In each case, the upper panel shows the times-series photometric data and the lower panel displays the orbital phased light curve with the fitted parabola around the time of maximum. The filled circles in the two panels refer to the data around the maxima and are used to calculate the times of light maximum, while the open circles to those not used for time determining. Lower panel: the part of the light curves obtained by TESS.
Download figure:
Standard image High-resolution imageMore recently, 14 times of light maximum were derived by Rios-Venegas et al. (2020) with light curves from the All-Sky Automated Survey (ASAS) and ASAS-SN and with their own photometric observations. All published times of light maximum were compiled by them and they improved the accuracy of the photometric ephemeris of KV Vel as following

By using this linear ephemeris (Rios-Venegas et al. 2020), the O − C (observed–calculated) curve of KV Vel is constructed with all available times of maximum light, which are listed in Table A1. The corresponding O − C plot is shown in the upper panel of Figure 2, where the red open circles and green and red dots refer to the newly determined times of light maximum by using the photographic (PG) data from DASCH, the ASAS-SN, and the TESS data, respectively. Blue dots represent the data collected from the literature.
Figure 2. Upper panel: the O − C diagram of KV Vel constructed with the linear ephemeris in Equation (4). The red open circles refer to the photographic (PG) data from DASCH, while red dots to those obtained from TESS. Blue and green dots represent times of light maximum collected from literature and derived from ASAS-SN. The solid magenta line suggests a combination of a revised linear ephemeris and a cyclic change. Middle panel: the O − C1 curve with respect to the revised linear ephemeris. Lower panel: residuals after all changes are subtracted.
Download figure:
Standard image High-resolution imageThe graph illustrates a periodic variation signal in the O − C curve, with a period of 29.55 yr and a semiamplitude of 0.0034 days, which can be explained as the light travel-time effect (LTTE) via the presence of a third body (Irwin 1952). Therefore, the solutions need a combination of a cyclic change with the eccentric orbit and a revised linear ephemeris (no linear period changes  ) to describe the O − C curve, namely
) to describe the O − C curve, namely

where ΔT0 is the correction to the initial epoch, ΔP0 is the correction to the initial orbital period, and E is the cycle number of light maximum. ν in Equation (5) is the true anomaly and E∗ is the eccentric anomaly. The two correlations, M = E∗ − esinE∗ and  , were used during the solution, where M is the mean anomaly and t is the time of light maximum. The time span of the data is much longer than the determined period of the LTTE, indicating the stability and reliability of the changes in the periodic oscillation. The plot of the O − C1 values with respect to the new linear ephemeris,
, were used during the solution, where M is the mean anomaly and t is the time of light maximum. The time span of the data is much longer than the determined period of the LTTE, indicating the stability and reliability of the changes in the periodic oscillation. The plot of the O − C1 values with respect to the new linear ephemeris,

is shown in the middle panel of Figure 2. The solid line in the panel is the theoretical orbit of KV Vel, which suggests a third body around the barycentre of this triple system. The explanations of all the parameters in Equation (5) and the values determined from the solution of LTTE are listed in Table 1.
Table 1. Orbital Parameters of the Third Body in KV Vel
| Parameters | Eccentric Orbit Case |
|---|---|
| Revised epoch, ΔT0 (day) | −0.0013 (±0.0003) |
| Revised period, ΔP0 (day) | 5.09 (±0.24) × 10−8 |
| Light travel-time effect semi-amplitude, A (day) | 0.0034 (±0.0004) |
| Orbital period, P3 (yr) | 29.55 (±0.16) |
| Longitude of the periastron passage, ω (deg) | 247.1 (±10.2) |
| Eccentricity, e | 0.67 (±0.11) |
Projected semimajor axis,  (au) (au) | 0.61 (±0.07) |
| f(m) (M⊙) | 0.00026 (±0.00008) |
Projected masses,  (M⊙) (M⊙) | 0.060 (±0.007) |
| Maximum distances, dmax | 9.35 (±2.41) |
Download table as: ASCIITypeset image
3. Physical Mechanisms for the Cyclic Period Change
The secondary component in KV Vel is a cool M-type star with a temperature of 3400 K and a mass of 0.23 M⊙. It is possible that the cyclic change in the O − C diagram is caused by the magnetic activity cycles of a cool component star (i.e., the Applegate mechanism; Applegate 1992). According to this mechanism, a certain amount of angular momentum is periodically transferred between different parts in the convection zone of the cool star. The rotational oblateness is then changing, which causes the orbital period to be variable as the cool star goes through its magnetic activity cycles. By using the same method of Qian et al. (2015), the required energies to produce the cyclic change in the O − C curve were computed for different shell masses of the cool component and are displayed in the left panel of Figure 3. With the radius of R2 = 0.40 R⊙ for the secondary given by Hilditch et al. (1996), its luminosity was computed by using  L⊙. The total energy radiated from the cool secondary in a whole active cycle (29.55 yr) is calculated and also displayed in the panel as the dashed line. It is shown that the total radiated energy is much smaller than the required energies of the Applegate mechanism, which suggests that this physical mechanism cannot explain the cyclic variation of the O − C diagram. Moreover, KV Vel was observed by TESS in four sectors from 2019 April to 2023 March. The TESS light curves are symmetric and rather stable and show no signs of magnetic activities for the cool component star.
L⊙. The total energy radiated from the cool secondary in a whole active cycle (29.55 yr) is calculated and also displayed in the panel as the dashed line. It is shown that the total radiated energy is much smaller than the required energies of the Applegate mechanism, which suggests that this physical mechanism cannot explain the cyclic variation of the O − C diagram. Moreover, KV Vel was observed by TESS in four sectors from 2019 April to 2023 March. The TESS light curves are symmetric and rather stable and show no signs of magnetic activities for the cool component star.
Figure 3. Left panel: the required energy to produce the cyclic oscillation in the O − C1 diagram by using Applegate's mechanism (solid blue line). The red dashed line represents the total energy that radiates from the secondary in a whole magnetic activity cycle (29.55 yr). Right panel: the phased O − C1 curve with respect to the new linear ephemeris that is caused by the presence of a low-mass companion to the central binary of the planetary nebula DS 1.
Download figure:
Standard image High-resolution imageSince the Applegate mechanism has difficulty explaining the cyclic period change, we analyzed KV Vel for the LTTE that arises from the gravitational influence of a tertiary companion. The presence of the third body produces the relative distance changes of the binary pair as it orbits the barycenter of the triple system. The phased O − C1 curve caused by the LTTE is displayed in the right panel of Figure 3. With the absolute parameters M1 = 0.63 M⊙ and M2 = 0.23 M⊙ (Hilditch et al. 1996), a calculation by using the following equation,

yields the mass function and the mass of the tertiary companion as: f(m) = 2.6(±0.8) × 10−4
M⊙ and  , respectively. G in the equation is the gravitational constant, while P3 is the period of the O − C1 oscillation. The projected radius of the central binary orbiting the barycenter of the triple system can be computed with the equation,
, respectively. G in the equation is the gravitational constant, while P3 is the period of the O − C1 oscillation. The projected radius of the central binary orbiting the barycenter of the triple system can be computed with the equation,

K is the amplitude of the cyclic change and c is the speed of light. When the orbital inclination of the third body is larger than 56.5°, the mass of the tertiary component corresponds to 0.06 M⊙ ≤ M3 ≤ 0.072 M⊙. In this case, the tertiary component can not undergo a stable hydrogen burning in the core, and it should be a brown dwarf. However, depending on the unknown orbital inclination of the third body, a low-mass stellar companion cannot be totally excluded.
4. Discussions and Conclusions
By using several photometric databases including DASCH (Grindlay et al. 2009, 2012), ASAS-SN (Shappee et al. 2014; Jayasinghe et al. 2019), and TESS (Ricker et al. 2015), a large number of times of light maximum have been determined. The O − C diagram is constructed with these new times of maximum together with those collected from the literature. It is discovered that the O − C curve shows a cyclic oscillation with a period of 29.55 yr and an amplitude of 0.0034 days. If the cyclic change is caused by the magnetic activity cycles of the cool component, the required energies are much larger than the total energy radiated from the cool secondary in a whole active cycle (29.55 yr). This suggests that the cyclic variation can not be explained by the Applegate mechanism. Therefore, we analyze the cyclic period oscillation for the LTTE that is caused by the wobble of the binary's barycentre via the existence of a third body. The mass function and the mass of the tertiary companion are revised as  , respectively. If the orbital inclination of the third body is larger than 56.5°, it should be a brown dwarf and it cannot undergo stable hydrogen burning in the core. By considering that the third body is coplanar with the central binary (i.e.,
, respectively. If the orbital inclination of the third body is larger than 56.5°, it should be a brown dwarf and it cannot undergo stable hydrogen burning in the core. By considering that the third body is coplanar with the central binary (i.e.,  ), the mass of the tertiary component is calculated as M3 ∼ 0.068 M⊙.
), the mass of the tertiary component is calculated as M3 ∼ 0.068 M⊙.
KV Vel is the central binary star of the PN DS 1 (Drilling 1983; Holmberg et al. 1978). Several investigators indicated that the initial primary in the progenitor of KV Vel filled its critical Roche lobe during the early AGB stage (e.g., Iben & Tutukov 1993). It had a small degenerate CO core with a helium-burning shell and an extended hydrogen-rich envelope (with initial mass in the range of 2.3–8 M⊙). Most of the hydrogen-rich envelope was ejected during the common envelope evolution, and the PN now around KV Vel is the ejected common envelope. The presence of the PN together with the extremely high temperature of the sdO primary suggests that it is one of the youngest postcommon envelope binaries (e.g., Aungwerojwit et al. 2007).
When the orbital inclination equals 90°, the orbital radius d3 of the tertiary component in the KV Vel triple system is about 9.35 au, which is much smaller than the size of the roughly circular PN (with a diameter of ∼180''). This indicates that the triple system is at the nuclei of the circular nebula. It is possible that the low-mass companion of KV Vel is formed during the ejection of the common envelope. The loss of the AGB envelope in the equatorial plane (e.g., Sandquist et al. 1998), followed by a spherical fast wind from the hot primary, will cause a great quantity of mass loss. The ejected common envelope formed the PN as well as the low-mass third body. KV Vel will evolve into normal cataclysmic variables (CV) through angular momentum loss (e.g., Shimansky et al. 2006). The substellar objects orbiting some CVs, such as V2051 Oph (Qian et al. 2015), DV UMa (Han et al. 2017), SW Sex (Fang et al. 2020), and HT Cas (Han et al. 2023), may also be formed during the common envelope evolution.
Acknowledgments
This work is supported by National Key R&D Program of China (grant No. 2022YFE0116800) and National Natural Science Foundation of China (grant Nos. 11933008, 11922306, 11703083, and 11903076). The continuous photometric data used in this study are collected by the TESS mission. Funding for the TESS mission is provided by NASA Science Mission Directorate. We really appreciate the TESS team for supporting this work. This work also makes use of the photographic data of DASCH and the ASAS-SN database.
Appendix
In Table A1, we present all the times of light maximum for KV Vel.
Table A1. All the Times of Light Maximum for KV Vel
| Times | Errors | E | O − C | Source | References | Times | Errors | E | O − C | Source | References |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (HJD 2400000+) | (±day) | (day) | (HJD 2400000+) | (±day) | day | ||||||
| 16120.26124 | 0.00666 | −83207 | −0.00103 | DASCH-PG | (1) | 59301.24577 | 0.00012 | 37710 | 0.00354 | TESS-CCD | (1) |
| 16818.05983 | 0.00632 | −81253 | −0.00039 | DASCH-PG | (1) | 59301.60270 | 0.00011 | 37711 | 0.00337 | TESS-CCD | (1) |
| 17456.57573 | 0.00691 | −79465 | −0.00176 | DASCH-PG | (1) | 59301.95983 | 0.00012 | 37712 | 0.00338 | TESS-CCD | (1) |
| 19171.78917 | 0.00862 | −74662 | 0.00003 | DASCH-PG | (1) | 59302.31672 | 0.00015 | 37713 | 0.00316 | TESS-CCD | (1) |
| 20187.77262 | 0.00682 | −71817 | −0.00176 | DASCH-PG | (1) | 59302.67403 | 0.00013 | 37714 | 0.00336 | TESS-CCD | (1) |
| 21234.46540 | 0.00672 | −68886 | −0.00591 | DASCH-PG | (1) | 59303.03111 | 0.00013 | 37715 | 0.00333 | TESS-CCD | (1) |
| 21858.69816 | 0.00608 | −67138 | −0.00591 | DASCH-PG | (1) | 59303.38817 | 0.00015 | 37716 | 0.00327 | TESS-CCD | (1) |
| 22619.34522 | 0.00710 | −65008 | −0.00861 | DASCH-PG | (1) | 59303.74516 | 0.00013 | 37717 | 0.00315 | TESS-CCD | (1) |
| 23908.88141 | 0.00931 | −61397 | −0.00589 | DASCH-PG | (1) | 59304.10240 | 0.00012 | 37718 | 0.00328 | TESS-CCD | (1) |
| 25416.25316 | 0.00704 | −57176 | −0.00628 | DASCH-PG | (1) | 59304.45959 | 0.00013 | 37719 | 0.00336 | TESS-CCD | (1) |
References: (1) This work; (2) Landolt & Drilling (1986); (3) Kilkenny et al. (1988); (4) Hilditch et al. (1996); (5) Rios-Venegas et al. (2020); (6) Ribeiro & Baptista (2011).
Only a portion of this table is shown here to demonstrate its form and content. A machine-readable version of the full table is available.
Download table as: Machine-readable (MRT)Typeset image






