The Simons Observatory: Beam Characterization for the Small Aperture Telescopes

Due to beam dilution, only a handful of natural point sources exist that are bright enough to calibrate the SAT beams. Of these, Jupiter is the brightest (Weiland et al. 2011; Planck Collaboration LII et al. 2017) and most suitable for SAT calibrations from the Atacama Desert. We focus on the characterization of the instrument's response to an unpolarized source as a baseline. The polarization response, which additionally requires a measurement of the instrument's polarization angle and cross-polar beam components, is left for future work.

Artificial calibration sources have the potential to overcome the limitations of the astrophysical sources. At the moment, sources mounted on tall structures have been successfully used for beam calibration (BICEP2/Keck Array XI et al. 2019). For the future, balloons (Masi et al. 2006), drones (Dünner et al. 2021), and even satellites (Johnson et al. 2015) are being considered. The use of drones for calibration purposes is the subject of multiple active studies (Nati et al. 2017). Calibration sources mounted on drones can be tuned in brightness, frequency, and cadence in order to meet the calibration requirements of different instruments. Additionally, these sources can be equipped with a polarizing wire grid that facilitates the calibration of polarization intensity and angle (Dünner et al. 2020). This last aspect is particularly important, as there are very few polarized astrophysical sources that are bright enough to calibrate the polarization response of the SO SATs (the highest upper limit of the planet polarization fraction, p_frac, is assigned to Uranus and corresponds to p_frac < 3.6% at 100 GHz within 95% confidence limits; Planck Collaboration LII et al. 2017).

There is a trade-off between calibrating with astrophysical and man-made sources. In the case of drones, flight endurance, especially in the thin atmosphere at high altitudes, is one of the main obstacles to successful calibration campaigns for experiments such as the SO. After recent on-site testing, the maximum flight time for the drone has been established to be ∼12 minutes (Coppi et al. 2022). For this reason, the nominal calibration strategy relies on the planets.

Figure 3 shows a comparison of the signal-to-noise ratio (S/N) we can achieve when observing some of the brightest planets and when observing a source mounted on a drone as a function of frequency. The S/N estimation relies on the source's power and takes into account the noise-equivalent power (NEP) and optical efficiency of the telescope while assuming the same integration time per pixel for all sources. When using the drone, we can expect a significantly higher S/N, which scales more smoothly with frequency compared to the various planets' cases. Note that the planets' brightness values are calculated as a function of their average estimated distance from the Earth in 2023. The exact calculations leading to the S/N values of Figure 3 are described in Appendix B.

Zoom In Zoom Out Reset image size

The simulated time-ordered data of the Jupiter observations are generated with the help of the Time-Ordered Astrophysics Scalable Tools (TOAST) ³¹ library, as well as the sotodlib ³² library, which interfaces with TOAST and provides experiment configuration files that are specific to SO.

The TOAST software was developed for simulating, gathering, and analyzing telescope time-ordered data. It is open-source software that is used in the framework of many current and next-generation CMB telescopes like LiteBIRD, Simons Array, SO, and CMB-S4. TOAST was used in a recent study of instrumental systematics for experiments aiming to observe the CMB polarization (Puglisi et al. 2021).

The software can generate instrumental noise, atmospheric noise, and scan-synchronous signals from ground pickup, as well as simulate the effect of an HWP. The code is end-to-end parallelized and optimized for low memory consumption, which facilitates its use with workload managers on large servers. TOAST allows one to simulate sky observations for different scan strategies of tunable parameters (scanning speed, observing time, and sky patch, among others) and implement various sky models.

The TOAST simulator module creates a focal plane configuration based on specified hardware parameters and samples the beam over a sky patch specified by the scheduler.

To simulate the atmosphere with TOAST, an additional file containing weather parameters is required. The corresponding module creates an atmospheric volume that moves with constant wind speed, set by the user or randomly drawn, and observed by individual detectors on the focal plane. This part of the code needs a set of input parameters, for example, for the detector gain, the field of view, and the center and width of the dissipation and injection scales of the Kolmogorov turbulence, describing atmospheric fluctuations (Kolmogorov 1941; Errard et al. 2015). In this work, we limit ourselves to an atmospheric model based purely on water vapor, as experience proves it is the dominant disruption for CMB experiments (Morris et al. 2022). Other potential absorbers, such as clouds, ice crystals, and oxygen, are left for future work.

For the Jupiter observations, we simulate constant elevation scans (CESs) to avoid systematic effects arising from varying the telescope's elevation, and we set a maximum allowed observing time of an hour. Given an observing site, time, and target, TOAST simulates observing schedules that conform to observing constraints such as elevation and boresight distance to the Sun and Moon. It uses the PyEphem ³³ software to predict the target's location with respect to the observatory. We run the scheduler with an allowed elevation range of [45°, 55°] and Sun/Moon avoidance radii set to 45°. The sampling rate and scanning speed are set to 200 Hz and 15 s⁻¹, respectively, at all times. The chosen maximum duration for a single CES facilitates tuning and calibrating the instrument; however, it takes Jupiter approximately 55 minutes to pass through the observing patch. After scheduling a single CES that follows these requirements, the scheduler moves on to the next day when Jupiter is available for observation. The simulated scans consider a single wafer (equipped with 860 detectors) each time instead of the full focal plane and cover an azimuth range of ∼20°. In practice, we will measure Jupiter with the HWP continuously spinning but we do not model it in the simulation. The signal amplitude from the sources is orders of magnitude greater than the polarized signal from the microwave sky; thus, we neglect this effect in the current simulations. Figure 4 shows the daily trajectory of Jupiter over the full months of 2021 June, July, and August, which we choose to simulate in terms of the planet's elevation as a function of time. Each curve is color-coded according to Jupiter's azimuth value. The 2D interval defined by the black dashed line refers to the observed region.

Zoom In Zoom Out Reset image size

It should be noted that the chosen azimuth and elevation ranges of the observing patch are not yet set in stone, and we expect them to evolve as we move closer to the telescope's deployment. This is because the choice of these parameters is primarily motivated by the source's availability during the observing period. The lower limit of the simulated elevation range is slightly lower than the most recent specifications, which set the nominal scanning elevation at 50°. As atmospheric loading worsens with decreasing elevation, our chosen strategy should be considered as a slightly pessimistic case, although we do not anticipate increasing the elevation range by 5° to improve our results significantly.

For the chosen observation period and scan strategy described above, we accumulated ∼50 hr of Jupiter simulations in total, as some days, the planet was not observable due to observing elevation and solar/lunar avoidance constraints. These simulations include atmospheric emission of both fixed and fluctuating weather parameters (see discussion in Section 5.3). For the scope of this project, we consider the atmosphere to be unpolarized even though it can intermittently carry a nonnegligible polarization fraction (Takakura et al. 2019). Furthermore, the simulations include realistic white and red detector noise expressed in noise-equivalent temperature. A detailed description of the noise model and parameters for the SATs can be found in Table 1 of Simons Observatory Collboration et al. (2019). For the planet temperature calculation, we rely on the thermodynamic temperatures listed in Table 4 of Planck Collaboration LII et al. (2017). The retrieved temperature values are then interpolated to the frequency range we wish to simulate and converted to T_CMB units, which express temperature in terms of the offset from the mean CMB temperature value.

The simulation of planet observations starts with the generation of signal time streams by using the TOAST and sotodlib software. The time streams include white and correlated noise and are produced for all detectors of each of the seven SAT focal plane wafers, as described in Section 3.3. However, the results shown in this paper only concern the center and one of the edge wafers. We gather all of the time streams simulated this way and construct 10° × 10° maps around the planet.

We do not use a standard maximum-likelihood mapmaker for this analysis. While these are, in principle, unbiased and optimal and would therefore appear to be an ideal choice for measuring the instrument beam, in practice, they are only unbiased if the data precisely follow the fitted model. In reality, this is never the case. In this case, unmodeled gain and pointing fluctuations mean that the observed signal is time-dependent in a way that a static image of the sky cannot capture. The result of such model errors is a bias that is typically at the subpercent level but is nonlocal and spread out by roughly a noise correlation length. This bias is large enough to completely overwhelm the fainter wings of the beam profile (Næss 2019).

To avoid this bias, we use a specialized filter-and-bin mapmaker that uses our knowledge of the planet's position to build a filter that removes as much of the atmosphere as possible while leaving the planet's signal almost untouched (see Hasselfield et al. 2013; Choi et al. 2020). In particular, if we assume that the planet's signal is entirely contained inside a mask with radius θ_mask around its location, and that the noise is correlated with covariance matrix C _n , then we can use all of the data outside of the mask to make a prediction about the noise inside the mask and subtract it (Lungu et al. 2022):

$$\begin{eqnarray}&&{\boldsymbol{d}}^{\prime} ={\boldsymbol{d}}-\mathop{\mathrm{argmax}}\limits_{{\boldsymbol{n}}}\ P({\boldsymbol{n}}| {{\boldsymbol{d}}}_{\theta \gt {\theta }_{\mathrm{mask}}},{{\boldsymbol{C}}}_{n}).\end{eqnarray} \tag{ 2 }$$

Here ${\boldsymbol{d}}^{\prime}$ and d are the raw and clean data vectors, respectively; n is the noise vector; and ${{\boldsymbol{d}}}_{\theta \gt {\theta }_{\mathrm{mask}}}$ are the data outside of the mask. To the extent that all of the signal is contained inside the mask, this subtraction will not introduce a bias. In practice, a small part of the signal will extend outside θ_mask, and there will be a trade-off between bias and noise subtraction (see discussion below).

For computational efficiency and to keep the implementation simple, we do not maximize P in Equation (2) but instead approximate it using the N_modes strongest principal components of a copy of d , where the area inside the mask has been filled in using polynomial interpolation. These principal components are then subtracted from the original d to form the cleaned ${\boldsymbol{d}}^{\prime}$. Effectively, we are using the detectors outside the mask at any given moment to predict what correlated noise the detectors inside the mask should be seeing and subtracting that. This approximation ignores the temporal correlations of the noise but seems to perform sufficiently well for our configuration.

After this cleaning, we assume that any remaining noise in ${\boldsymbol{d}}^{\prime}$ is uncorrelated and can be mapped using a simple inverse-variance-weighted binned mapmaker. Note that the resulting map is only low-bias inside the masked region θ < θ_mask. Any data outside θ_mask are effectively high-pass-filtered due to the noise subtraction and thus heavily biased.

The effectiveness of this method depends strongly on the signal being compact (so one can use a small θ_mask) compared to the correlation length of the noise. It is therefore best suited for high-resolution telescopes like ACT or the SO Large Aperture Telescope but still performs reasonably well for the SO SAT.

The mask radius, θ_mask, around the source and the number of modes, N_modes, can be tuned to optimize the performance of the algorithm. As the noise levels are estimated from the region that remains unmasked, a too-small θ_mask might result in subtracting beam power of substantial amplitude, while one might fail to properly capture the relevant noise modes with a too-large θ_mask. The top panel of Figure 5 shows the principal component analysis (PCA) eigenvalues of some of the 300 strongest modes for a single observation performed with the 93 GHz frequency band beam model and fixed precipitable water vapor (PWV). Even though the total number of estimated modes equals the number of simulated detectors (860 detectors per single-wafer simulation), we find this truncated sample representative enough to capture the rate of the eigenvalues' decreasing amplitude. Each data point in this plot corresponds to the average eigenvalues of all of the detectors of the center wafer of the focal plane. The large value of the first mode presented in this figure (∼2 orders of magnitude larger than the next mode) indicates how the atmospheric noise may be crudely approximated as a single correlated mode. The bottom panel of Figure 5 presents the noise amplitude of the same 93 GHz planet map estimated as the standard deviation of all of the data points included in the outer 10% of the mask as a function of the number of subtracted modes. The results illustrate an overall reduction of the noise amplitude with an increasing number of modes in an almost monotonic fashion. The noise variance is shown to be statistically compatible with zero after subtracting ∼300 modes.

Zoom In Zoom Out Reset image size

The outer scale of atmospheric turbulence is observed to be significantly smaller than the 12° field of view of a single SAT wafer (Errard et al. 2015). Splitting the wafer into subsets of fewer detectors and estimating the correlated modes across these subsets instead would likely adequately capture the atmospheric noise model with a smaller number of modes than in the case of estimating the noise correlations from the full wafer. Relevant modifications to the mapmaking pipeline will be made, if necessary, when we start observations.

We set θ_mask to be equal to a radius, outside of which the beam power has fallen below ∼0.01% of its peak value, following the example of Lungu et al. (2022). Figure 6 shows some of the binned modes that were calculated from the PCA analysis for the same simulation. The first mode shows the atmospheric emission amplitude scaling with telescope boresight elevation, as expected, while the rest of the modes of the top row probe stripy patterns in slightly different directions and scales. The bottom row shows modes corresponding to detector correlations of significantly smaller amplitude. Subtracting these faintest modes might be excessive and could, in turn, end up negatively impacting the performance of the beam model reconstruction algorithm. Figure 5 suggests that the most suitable number of modes to subtract should be of the order of 10.

Zoom In Zoom Out Reset image size

It is interesting to look at the impact of subtracting a different number of correlated modes directly on planet maps. Figure 7 shows a single, 93 GHz, 4° × 4° planet map after subtracting the 1st, 2nd, 3rd, 4th, 30th, 100th, 150th, and 300th modes, following the reasoning of Figure 6. From this multipanel plot, we see the atmospheric striping starting to subside after the ∼fourth mode, while the contrast between the masked and unmasked region becomes more pronounced with increasing number of subtracted modes. As expected, the faintest eigenmodes of the covariance matrix will better capture the noise of the unmasked region, since the eigenmodes are estimated in this region. Consequently, subtracting these faint modes from the maps will lower the noise amplitude in the unmasked region but not impact the masked region around the source as much.

Zoom In Zoom Out Reset image size

For the beam profile fitting of the planet observations, we closely follow the method developed for the ACT​​​​​ (Lungu et al. 2022). The beam fitting method is implemented in beamlib, a version of the code from the work of Lungu et al. (2022) that has been adjusted to SO hardware specifications. This section summarizes the main aspects of the method.

The fitting pipeline takes a set of input maps and trims them to a size that should refer to a region well contained inside θ_mask. The next step is to correct for the bias caused by the noise mode subtraction. As in the case of the ACT beams, we find this effect to be fairly consistent with a constant offset deviation of the beam wing from the 1/θ³ function that the input SAT beams approximately follow (see Section 2). For the constant offset estimation, we use a relatively "flat" part of the beam profiles (where the oscillatory side-lobe pattern is not as pronounced), and the beam power has fallen below ∼0.1% of its peak value. The best-fit value for this offset is computed for each observation and then subtracted from each observation before averaging the beam profiles.

The core (main) beam is fitted, employing the basis functions from Lungu et al. (2022),

$$\begin{eqnarray}&&{f}_{n}(\theta {{\ell }}_{\max })=\displaystyle \frac{{J}_{2n+1}(\theta {{\ell }}_{\max })}{\theta {{\ell }}_{\max }},\end{eqnarray} \tag{ 3 }$$

where J_2n+1 are Bessel functions of the first kind, n is a nonnegative integer, and ${{\ell }}_{\max }$ is allowed to vary around some mean value defined by the beam resolution. The angle of the transition from the "core" to the "wing" region of the beam is specified by the user, yet it is allowed to vary slightly in the code in order to retrieve its optimal value. The reconstructed beam transfer function is calculated as the Legendre transform of the best-fit model,

$$\begin{eqnarray}&&{b}_{{\ell }}=\displaystyle \frac{2\pi }{{{\rm{\Omega }}}_{B}}{\int }_{-1}^{-1}B(\theta ){P}_{{\ell }}(\cos \theta )d(\cos \theta ),\end{eqnarray} \tag{ 4 }$$

where ${P}_{{\ell }}(\cos \theta )$ are the Legendre polynomials, Ω_B is the beam solid angle, and B(θ) is the best-fit radial beam profile comprised of the core and wing fit. Besides the best-fit harmonic transform, beamlib also calculates the eigenmodes of the beam fitting covariance matrix, which we will refer to as error modes throughout the paper.

A small number of available planet observations can be problematic when estimating the bin–bin covariance matrix of the binned radial profile. For that reason, the code employs a shrinking technique. The idea behind the approach is the following: the level of down-weighting of the off-diagonal components of the covariance matrix should depend on the number of available observations. This approximation is parameterized by the so-called shrinkage intensity, ${\hat{\lambda }}^{* }$ (see Equation (A5), Appendix A, Lungu et al. 2022). The shrinkage intensity is applied to a biased version of the covariance matrix, T , where we have set all the off-diagonal components to zero and the empirical, unbiased covariance matrix, S , to synthesize the "shrunk" covariance matrix, C , that we will use for the beam fitting as (Equation (A6), Appendix A, Lungu et al. 2022)

$$\begin{eqnarray}&&{\boldsymbol{C}}={\hat{\lambda }}^{* }{\boldsymbol{T}}+(1-{\hat{\lambda }}^{* }){\boldsymbol{S}}.\end{eqnarray} \tag{ 5 }$$

One can easily conclude that the larger the number of observations, the closer we can get to an unbiased covariance estimation. Figure 8 shows the value of λ* as a function of the number of input observations to the beam fitting code for our frequency bands. The shrinkage intensity seems to converge to a value of ≈0.1 for a set of N_obs = 50 observations in all cases.

Zoom In Zoom Out Reset image size

The beam fitting performance is tightly linked to our ability to sufficiently suppress the atmospheric signal, which, in turn, depends on the number of correlated noise modes one removes from the data. For the simulation setup we employed, we find that the number of correlated modes that need to be removed typically lies between N_modes = 5 and ​​​​​50 for the frequency bands we consider.

The choice of the number of subtracted modes relies on a combination of different criteria, as summarized in Figure 9. The top panel shows the linear bias in multipole space between normalized fitted and input beam transfer function as a function of the number of modes removed (varying colors) for simulations performed at the 93 GHz frequency band. The middle panel shows the corresponding real-space variance between planet maps for the different number of modes subtracted. Each curve shown in this panel is estimated by computing the per radial bin variance of the beam profiles of a set of maps that have the same number of correlated modes removed. The bottom panel of the figure refers to the best-fit beam profiles of the same planet sets along with the input beam model.

Zoom In Zoom Out Reset image size

From the middle panel, we see that the logarithmic variance between different observations consistently reduces with an increasing number of subtracted modes, but after some mode (N_modes ≳ 20), it starts increasing again. We expect the strongest noise modes to be quite similar between simulations assuming different dates, but fainter modes should reflect some degree of day-to-day atmospheric changes. Subtracting these fainter modes inevitably increases the variance between different maps to some extent. Such behavior can indicate that we should not remove any more modes to avoid the risk of also subtracting signal along with the noise.

The chosen number of modes, N_modes, should be the best combination of low bias and low variance, which is the case for N_modes = 10–20. Ideally, we would like the bias of the fitted beam transfer function to be fairly constant across the different multipole bins. We decide to use N_modes = 10 for the 93 GHz case.

Higher-frequency bands require more modes to be removed, since the atmospheric brightness scales with frequency. For 145, 225, and 280 GHz, we find that the number of modes that best satisfies our selection criteria is N_modes = 10, 30, and 40, respectively. Depending on the different simulation parameters, one might find a preferred (narrow) range of modes instead of a single global value. An alternative approach would be to subtract all of the correlated modes and estimate a transfer function for the bias caused by this process by running additional simulations. For this work, we aim to only mildly bias our data so that the nature of this bias is fairly predictable and, in turn, easily corrected.

The fidelity of the beam reconstruction process depends on the input beam models. The input models depend, in turn, on the position of the detector on the focal plane. To assess the impact of the detector position on the fitting performance, we use beam models for a pixel on the center and the edge of the focal plane. In both cases, we bin the data into maps with the 10 most correlated modes removed after masking and gap-filling a region that extends to a radius of θ_mask = 25 around the source. The gap-filling is done with polynomial interpolation of the unmasked data over the masked region.

Figure 10 shows the reconstructed beam profiles from a set of 3 months of simulated Jupiter observations for the center (orange curve) and one of the edge wafers (green curve). The detectors of the center wafer share the center pixel beam model, while those of the edge wafer are assigned the edge pixel beam model (as discussed in Section 2). The selection of the exact edge wafer is not important, as the Ticra Tools setup is radially symmetric with respect to any of the edge pixels of the telescope's focal plane (see Figure 1). The atmospheric PWV was set to ∼1 mm at all times, and we did not allow for wind speed variations. The results show the fitted center pixel beam model following the input model closely, up to ∼four times the beam size (FWHM = 27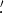4 at 93 GHz), while the edge pixel beam profile deviates slightly from the input toward the largest radial bins.

Zoom In Zoom Out Reset image size

Figure 11 quantifies the above statement in terms of the bias on the beam transfer functions of the two reconstructed beam profiles compared to the input beams. From the figure, we can see that, while the center pixel model reconstruction is better, the transfer function bias remains well under 1.5% for a multipole range of ℓ = 30–700 for both cases.

Zoom In Zoom Out Reset image size

Different atmospheric conditions could affect the performance of the beam reconstruction algorithm. During the chosen observation period, we expect the weather conditions to vary to some extent. Generally speaking, there are a variety of parameters driving the atmospheric behavior. From these parameters, the amount of PWV has the strongest impact on the atmospheric emission (see, e.g., Dünner et al. 2012; Errard et al. 2015).

The impact of PWV on atmospheric transmission can be seen in Figure 1 of Errard et al. (2015). We define the transmission at some frequency, ν, as the ratio ${ \mathcal T }(\nu )\,\equiv I(\nu )/{I}_{0}(\nu )$ of the radiation received by the detector, I(ν), and the radiation above the atmosphere, I₀(ν). A high PWV value implies a low transmission ${ \mathcal T }(\nu )$, which can be defined as the negative exponent of the air mass, m(90° − el), times some standard value of the optical depth, τ₀, measured at the zenith (Errard et al. 2015),

$$\begin{eqnarray}&&{ \mathcal T }(\nu )={e}^{-m(90^\circ -\mathrm{el}){\tau }_{0}},\end{eqnarray} \tag{ 6 }$$

where el is the elevation. The air mass is, in turn, computed as a function of the zenith angle (see Equation (2) of the same paper). This relationship holds at high elevations if we model the atmosphere as a parallel planar slab; in this case, $m(90^\circ -\mathrm{el})\approx 1/\sin (\mathrm{el})$. The atmospheric transmission contributes to the total loading, ${ \mathcal E }(\nu )$, as follows (Errard et al. 2015):

$$\begin{eqnarray}&&{ \mathcal E }(\nu )=[1-{ \mathcal T }(\nu )]{B}_{\nu }({T}_{\mathrm{atm}}).\end{eqnarray} \tag{ 7 }$$

In the above, B_ν (T_atm) is the spectral radiance of a blackbody of temperature equal to the atmospheric temperature, T_atm.

Figure 12 shows the binned time-ordered data of a single Jupiter observation, including atmospheric emission of PWV = 0.5 mm (left column) and PWV = 2.5 mm (right column) at 93 (top row) and 280 (bottom row) GHz. The data are binned after subtracting the mean (atmospheric) temperature and have no correlated modes removed. The atmospheric intensity and therefore striping is shown to increase nonnegligibly with PWV value, as expected. For the cases presented, the S/N at 0.5 (2.5) mm is estimated as S/N = 35 (30) for the 93 GHz band and S/N = 140 (60) for the 280 GHz band.

Zoom In Zoom Out Reset image size

The atmospheric signal is strongly correlated between different detectors. The wind speed and direction impact the correlation length along with the outer scale of turbulence and scan strategy. For two detectors with beam centroids that lie parallel to the wind direction, we will observe maximum signal correlation (Equations (23)–(26) of Morris et al. 2022). To explore these effects, we run simulations for a center pixel in the 93 GHz frequency band and the different cases of atmospheric parameters described in Table 2.

The PWV value, wind speed, and direction are either fixed or allowed to fluctuate around a mean value following some distribution that is consistent with historical distributions according to MERRA-2 (Global Modeling & Assimilation Office (GMAO) 2015) for the Atacama observation site. These distributions are included in TOAST and specified per hour of the day and month. The mean and standard deviation values quoted in Table 2 are synthesized from the individual simulations of the full observing period we have chosen.

Notice that the estimated fixed mean PWV value strongly agrees with the one motivated by seasonal data of the ACT telescope (∼1 mm), which is located at the SO observation site (see Figure 4 of Morris et al. 2022). The simulated PWV is uniformly distributed, and the surface temperature and pressure are kept constant at 270 K and 530 hPa, respectively. The wind speed values in Table 2 have a positive or negative sign in order to also incorporate the wind direction.

Figure 13 shows the uncertainty of the reconstructed beam transfer function with respect to the input beam model for cases (ii), (iii), (iv), and (v), as described in Table 2, in the form of blue, orange, green, and red error bars, respectively. The mean bias of the nominal case, (i), is demonstrated with a black dashed line surrounded by a gray shaded uncertainty band for reference. The error bars are shown per 40 multipoles for easier visualization and extend to a multipole number of ${{\ell }}_{\max }=700$. The beam fitting performance is rather stable across the different weather cases we have considered. However, the quality of the results slightly worsens with added atmospheric complexity, with the largest error bars of Figure 13 corresponding to the case where both PWV and wind speed are allowed to fluctuate (case (v)). A large PWV value implies an increased temperature of the atmospheric brightness. Since the latter also scales with frequency, the quality of the results depends on the ratio between the planet and atmospheric brightness at the frequency band of interest and how efficiently we can suppress the correlated noise. Nevertheless, we should highlight that, for all atmospheric parameters chosen, we were still able to recover the input beam with an uncertainty smaller than ∼1.5% in all cases for the multipole range ℓ = 30–700 (for 93 GHz).

Zoom In Zoom Out Reset image size

The beam reconstruction algorithm depends on the number of available observations. To probe this, we present the accumulated S/N as function of the number of Jupiter simulations for four different frequency bands centered on 93, 145, 225, and 280 GHz. The beam models in the simulations assume a detector placed at the center of the focal plane.

In our analysis, we face a trade-off between the overall accuracy of the reconstructed beam model and extending the model to larger angles. The S/N obviously decreases as we move away from the center of the beam. Therefore, our attempts at fitting beam models in the faint wings of the sidelobes can sometimes bias our overall results. Assessing the reconstruction noise as a function of the number of observations is essential for optimizing the planet observing strategy. Figure 14 shows the estimated S/N for all frequency bands when the number of available observations ranges from 5 to 50. The circles refer to S/N values estimated by determining the noise that remains in the planet maps, which is approximated as the standard deviation of the data in the outer 10% of the mask. The dashed lines are the fits of the S/N values to an underlying $A\sqrt{{N}_{\mathrm{obs}}}+B$ model (for some constants A and B), which is the statistical behavior we would expect. Based on Figure 14, we decide that attempting to model all frequency bands down to −35 dB is a reasonable choice. This value matches the acquired S/N for the lowest frequency band when the full observation set is employed and translates to a mask radius θ_mask ∼ 5 θ_FWHM for the 93 GHz case. For consistency, we also use θ_mask ∼ 5 θ_FWHM for the other frequency bands.

Zoom In Zoom Out Reset image size

Figure 15 shows the reconstructed beam profiles for the four frequency bands compared to their input models. From the figure, we see the beam profiles of the MF and UHF bands following different side-lobe patterns in the target region. The beamlib code adapts to these differences by optimizing the interplay between the Bessel function basis model, which fits the beam core (where the side-lobe structure is expected to be more pronounced), and the 1/θ³ fit of the beam wing. The transition from core to wing fit is denoted with a black vertical line. Of all frequency bands, the 280 GHz band has the largest uncertainty on the reconstructed beam profile. The corresponding harmonic transform errors and their uncertainty, as calculated from beamlib, are presented in Figure 16. The plot shows a bias that roughly decreases in amplitude with increasing band center frequency, especially for the multipole range 100 < ℓ < 300, and remains under ∼1.3% at all times. Table 3 shows the maximum values of the reconstructed beam transfer function error, $\delta {B}_{{\ell }}=({B}_{{\ell }}^{\mathrm{fit}}/{B}_{{\ell }}^{\mathrm{in}})-1$, for all frequency bands for both the full and a slightly truncated multipole range, which will be further evaluated for calibration against Planck data in Section 5.6.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

The multipole region at which B-modes are expected to peak is still well contained within the truncated multipole range. The bias on the solid angle estimation, δΩ = (Ω^fit/Ωⁱⁿ) − 1, from beamlib is also shown.

These results reflect not only the expected scaling of the S/N as a function of frequency (and associated beam size) but also the success of the basis function choice for the beam model. This argument becomes evident when looking at the ringy pattern of the 93 GHz band transfer function bias and associated uncertainty. Notice that the uncertainty of the reconstructed beam transfer function reduces as the number of available input simulations (and therefore accumulated S/N) increases. An estimate that quantifies this statement is provided in Appendix C.

The technique chosen for the absolute calibration of the beam transfer functions will impact the ℓ-dependence of the bias. Calibrating the SAT beam transfer function against previous CMB experiments, such as Planck, is carried out by matching the spectra of the two telescopes over a limited range of multipoles. Since B-modes are expected to peak at a multipole number of ℓ ≈ 80, a calibration range around this lower multipole region is naturally motivated.

We test the impact of different calibration choices directly on the bias of the reconstructed beam transfer function compared to the input. We do this by drawing 10⁴ realizations, ${B}_{{\ell }}^{{\prime} }$, of the reconstructed beam transfer function ${B}_{{\ell }}^{{\rm{fit}}}$ and the first 10 error modes $\delta {B}_{{\ell }}^{(i)}$:

$$\begin{eqnarray}&&B{{\prime} }_{{\ell }}^{j}={B}_{{\ell }}^{{\rm{fit}}}+\displaystyle \sum _{i=1}^{10}{c}_{i,j}\delta {B}_{{\ell }}^{(i)},\hspace{0.8cm}j=1,..,{10}^{4}.\end{eqnarray} \tag{ 8 }$$

The weights, c_i,j , are randomly drawn from a normal distribution of zero mean and standard deviation equal to 1.

Given the SAT beams and expected transfer function, the multipole range that facilitates the absolute calibration of the SAT maps using the Planck data will likely lie within ${{\ell }}_{\min }=50$ and ${{\ell }}_{\max }=200$. To investigate the impact of different choices of calibration range, we slice this multipole range and calibrate each one of the beam realizations we produced over the ranges ℓ = 50–100, 50–200, and 100–200 by minimizing the difference between the output and input beam over each range. Figure 17 shows the 1σ error band of the 10⁴ newly calibrated beams, divided by the input beam transfer function, for the three multipole range choices quoted above. The results are shown for all four frequency bands (increasing in frequency from top to bottom) and are truncated to ℓ = 10–300 for visualization purposes. As one can conclude from the plots, assuming a calibration range of ℓ = 50–100 results in the minimum beam uncertainty at the low-multipole range of interest, while a calibration range at higher multipoles significantly increases the beam uncertainty at low multipoles.

Zoom In Zoom Out Reset image size

The SO SATs allow us to constrain the tensor-to-scalar ratio, r, with a statistical error of σ(r) ≤ 0.003. Beam modeling errors can bias cosmological analysis, and it is therefore appropriate to briefly consider their impact on the forecasted value of r. For this purpose, we employ the BBpower software, ³⁴ which is part of the publicly available SO analysis pipeline (Wolz et al. 2023). BBpower is a harmonic-based component separation algorithm that has been adapted to the specifications of the SO telescopes (Simons Observatory Collboration et al. 2019). We use the code to forecast sensitivity to the value of the tensor-to-scalar ratio through Fisher analysis (Fisher 1922).

To quantify the effect of the beam reconstruction bias and uncertainty, we use Equation (8) to create 100 biased beam realizations for each of the four frequency bands considered in our analysis. For each beam realization, we construct a set of beam-convolved CMB and foreground spectra assuming no primordial B-modes (r = 0). The sky component and noise power spectra follow "Pipeline A" with the "baseline" noise level and "optimistic" 1/f noise description in Wolz et al. (2023). We then forecast the reconstructed r-value for each of the 100 realizations by (incorrectly) using the unbiased input beam to perform beam deconvolution in the Fisher forecast code. The resulting bias on the tensor-to-scalar ratio is Δr = 1.08 × 10⁻⁴. This number can be compared to the expected 1σ error on r, which is σ(r) ≈ 3 × 10⁻³ (Simons Observatory Collboration et al. 2019). These beam errors add insignificantly to the overall variance on r: σ(r)^extra ∼ 10⁻⁶. We thus conclude that the beam reconstruction error achieved with the setup presented in this work will be small enough to not significantly bias the SO r-measurement.

Variations in the detector passband will impact the shape of the effective beam and therefore affect the performance of the fitting algorithm. While we leave the detailed analysis of this phenomenon for future work, it is useful to show how the input beam models may change under the assumption of nonuniform passbands. As stated in Section 2, the frequency band beams are produced by combining five monochromatic beams within a 20% bandwidth around the center frequency with a top-hat passband. We compare the profile of the beams that were constructed this way to the ones where, instead of a top-hat function, we employed the simulated passbands from Abitbol et al. (2021) and show the results in Figure 18 for all frequency bands.

Zoom In Zoom Out Reset image size

Any difference between the uniformly and nonuniformly weighted beam profiles is negligible, at least to the ∼−35 dB level we have chosen for fitting the SAT beams. Consequently, there is no indication from these plots that any change to the beam fitting method would be necessary. The passband assumptions/simulations we make will eventually be replaced with Fourier transform spectroscopy measurements to characterize the instrument's spectral response. These measurements will enable us to produce realistic SAT beam models for future analysis.

The instrumental beam can be frequency-scaled in a way that matches the spectral energy distribution (SED) of the different sky components that the telescope observes. Properly accounting for this effect is important for the performance of foreground component separation algorithms. Assuming a known passband, τ(ν), of the instrument, the frequency-averaged beam, B(θ, ϕ), can be described as

$$\begin{eqnarray}&&B(\theta ,\phi )=\int B(\theta ,\phi ,\nu )\tau (\nu )S(\nu )d\nu ,\end{eqnarray} \tag{ A1 }$$

where B(θ, ϕ, ν) is a monochromatic beam at frequency ν, and S(ν) captures the assumed frequency scaling. For many astrophysical sources, the latter can be expressed as a power law,

$$\begin{eqnarray}&&S(\nu )={\left(\displaystyle \frac{\nu }{{\nu }_{c}}\right)}^{\beta },\end{eqnarray} \tag{ A2 }$$

where ν_c is the frequency band center, and β is the spectral index. We consider four cases of frequency scaling matching the SED of the CMB, planets, galactic dust, and synchrotron emission, corresponding to spectral index values of β_CMB = 1, β_planet = 2, β_dust = 1.56, and β_sync = −3 (Planck Collaboration et al. 2020). The beam profiles for these four cases, along with the case where no frequency scaling was implemented, are shown in Figure 19 for all four frequency bands.

Zoom In Zoom Out Reset image size

It is interesting to see how the frequency scaling impacts the beam transfer function. Figure 20 shows the ratio of the beam transfer function of the four chromatic beams described above and the one of the nominal case where no frequency scaling was implemented. The chromaticity effect is smooth across all frequency bands and decreases in amplitude with increasing frequency. In the case of the 93 GHz band, not taking account of the beam frequency scaling can result in a transfer function bias as large as ∼10% at ℓ = 700.

Zoom In Zoom Out Reset image size