OGLE-2017-BLG-0406: Spitzer Microlens Parallax Reveals Saturn-mass Planet Orbiting M-dwarf Host in the Inner Galactic Disk

The microlensing event OGLE-2017-BLG-0406 was first discovered on March 27 (HJD' = HJD-2,450,000 = 7839) by the Optical Gravitational Lensing Experiment (OGLE) collaboration at (R.A., decl.)(J2000)=(${17}^{{\rm{h}}}{55}^{{\rm{m}}}59\buildrel{\rm{s}}\over{.} 92$, $-29^\circ 51^{\prime} 47\buildrel{\prime\prime}\over{.} 3$) or (l, b) = (03601, − 24164) in Galactic coordinates, as alerted by the OGLE Early Warning System (Udalski 2003). The event lies in the OGLE-IV field BLG506, and the observations were conducted at the cadence of once per hour by using the 1.3 m Warsaw telescope located at Las Campanas Observatory in Chile, equipped with a 1.4 deg² field-of-view CCD camera. The Microlensing Observations in Astrophysics (MOA) group independently discovered this event on May 5 (HJD' = 7879) by using the MOA alert system (Bond et al. 2001) and identified it as MOA-2017-BLG-233. MOA observed this event with 15 minutes cadence by using MOA-II telescope at Mt. John University Observatory in New Zealand, equipped with 2.2 deg² field-of-view camera MOA-camIII (Sako et al. 2008). Most observations were conducted in the customized MOA-Red wide band, which is the sum of the standard Cousins R and I bands with occasional observations in the Johnson V band. The event was also independently discovered as KMT-2017-BLG-0243 by the Korean Microlensing Network (KMTNet: Kim et al. 2016) survey using its post-season event finder (Kim et al. 2018). KMTNet observes toward the Galactic bulge by using three 1.6 m telescopes equipped with 4 deg² camera at the Cerro Tololo Inter-American Observatory in Chile (CTIO: KMT-C), the South African Astronomical Observatory in South Africa (SAAO: KMT-S), and the Siding Spring Observatory in Australia (SSO: KMT-A). Because this event was in an overlapping region between two fields (KMTNet BLG02 and BLG42), the observations were conducted at a 15 minute cadence.

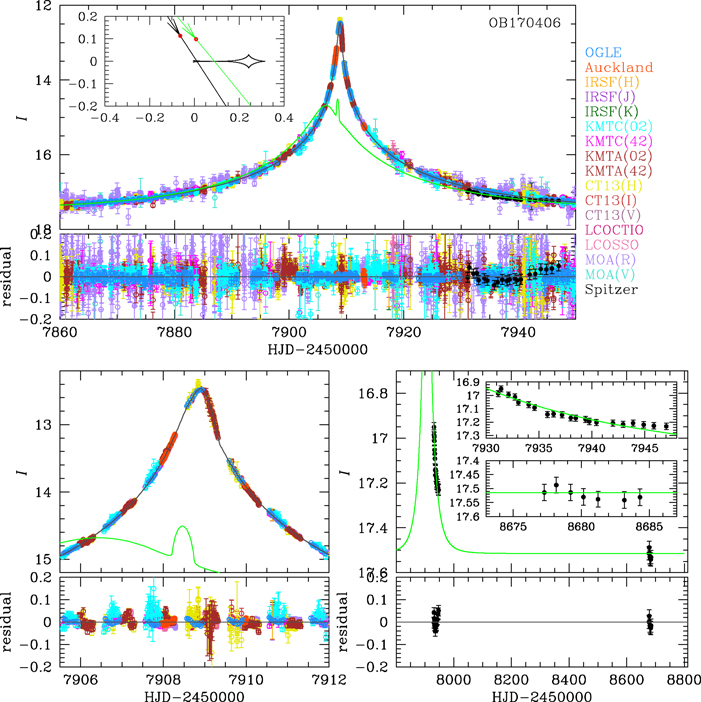
On June 2 (HJD' = 7907), the Microlensing Follow-up Network (μFUN) collaboration issued an alert that the event was peaking at a high magnification, which means that there is a high probability that the light curve will show an anomaly if the lens star hosts a planet (Griest & Safizadeh 1998). After the alert, μFUN, the Microlensing Network for the Detection of Small Terrestrial Exoplanet (MiNDSTEp) collaboration and Las Cumbres Observatory (LCO) global network of telescope collaboration started high-cadence follow-up observations. μFUN used the following telescopes: the 1.3 m CTIO telescope in Chile, the 0.41 m Auckland telescope and the 0.36 m Farm Cove telescope in New Zealand, and the 0.30 m Perth Exoplanet Survey Telescope (PEST), and the 0.25 m Craigie telescope in Australia. MiNDSTEp used the 1.54 m Danish Telescope at La Silla Observatory in Chile. LCO used the 1.0 m telescopes at CTIO in Chile and at SSO in Australia. Figure 1 shows the light curve of the event.

Zoom In Zoom Out Reset image size

On June 4 (HJD' = 7909), deviations from a single-lens fit were noticed just after the peak by the MOA observer. Then the first planetary model was circulated by V. Bozza, and it was confirmed by several modelers. Because the event was very bright (∼12.5 mag in I band), some images taken with normal exposure time by survey telescopes were saturated.

We also obtained three near-infrared images taken at different epochs (HJD' ∼ 7911, 7918 and 7942). The observations were made with SIRIUS, a simultaneous imager in J, H, and K_S bands, covering an area 7.7 × 7.7 arcmin² with a pixel scale of 045 (Nagayama et al. 2003) on the 1.4 m InfraRed Survey Facility (IRSF) telescope at SAAO. The observations were conducted to measure the source color rather than for light-curve modeling. The data sets are listed in Table 1.

Table 1.  The Data Sets Used to Model the OGLE-2017-BLG-0406 Light Curve and the Error Correction Parameters

Telescope	Filter	${N}_{\mathrm{use}}/{N}_{\mathrm{obs}}$	k	${e}_{\min }$
OGLE	I	6185/6185	1.441	0.003257
MOA	Red	14611/14611	1.970	0.003257
	V	315/315	1.794	0.003257
KMT-C02	I	1558/1558	2.537	0.003257
KMT-C42	I	1713/1713	1.897	0.003257
KMT-A02	I	1903/1903	2.590	0.003257
KMT-A42	I	2068/2068	2.550	0.003257
KMT-S02	I	0/2485
KMT-S42	I	0/2481
Danish	I	0/200
LCO-CTIO	I	296/296	1.323	0.003257
LCO-SSO	I	464/464	1.644	0.003257
Auckland	R	82/82	2.280	0.003257
Craigie	clear	0/677
Farm Cove	clear	0/31
PEST	clear	0/262
CTIO	I	21/21	0.860	0.003257
	V	7/7	0.760	0.003257
	H	92/93	1.700	0.003257
IRSF	J	3/3	1.000	0.000
	H	3/3	1.000	0.000
	KS	3/3	1.000	0.000
Spitzer	L	21/21	3.120	0.003257

Download table as:  ASCIITypeset image

OGLE-2017-BLG-0406 was observed by the Spitzer space telescope with the 3.6 μm (L-band) channel of the IRAC camera. Spitzer started to observe this event on June 26 (HJD' = 7931), which was about 3 weeks after the peak because this was the first date that the target was visible in the Spitzer image. This event was chosen for Spitzer observations as part of a long-term (2014–2019) program, according to the protocols of Yee et al. (2015a). Specifically, it met objective criteria defined by Yee et al. (2015a), which meant that it had to be chosen for observations and observed at a specified cadence, independent of whether it had a planet or not. Accordingly, it was observed approximately once per day for the first 4 weeks, but not the final 2 weeks of the program in 2017.

In 2019 (i.e., the final Spitzer microlensing season), essentially all planetary events from 2014 to 2018 were observed for about a week at baseline, primarily to check for systematics in the light curves, in part because of concerns raised by Koshimoto & Bennett (2019). See Gould et al. (2020) for further discussion. OGLE-2017-BLG-0406 was observed seven times under this program, meaning that there are a total of 28 data points. As discussed in Section 9.1, these seven points must be excluded when determining whether OGLE-2017-BLG-0406Lb can enter the Spitzer-statistical sample. For the role of these data in the analysis of systematic effects, see the Appendix.

In principle, we could now proceed to incorporate the Spitzer data into a joint fit together with the ground-based data. We will do so in Section 5.2. First, however, it is important to examine how the Spitzer data and the ground-based data contribute information to the parallax measurement. The principal reason for doing so is that both data sets can be subject to systematic errors, which are of very different types and can affect the parallax measurement very differently. An important check for such systematics is whether the parallax information derived from each data set is consistent with the other. Failure of this test would provide clear evidence for systematics in one or both data sets. In addition, we will ultimately be making somewhat separate use of the magnitude and direction of the parallax vector. In order to understand how secure each of these components is, we will need to trace their origins in different combinations of Spitzer-based and ground-based information.

In Section 4, we showed that the ground-based data yielded essentially one-dimensional parallax information, with ${\pi }_{{\rm{E}},\parallel }$ (the component parallel to the instantaneous projected direction of the Sun at t₀) measured about nine (for W+) or five (for W-) times more precisely than the orthogonal component ${\pi }_{{\rm{E}},\perp }$. This is because the information for the latter comes from further out in the wings of the light curve (Smith et al. 2003; Gould 2004), which, for events like OGLE-2017-BLG-0406 that are not extremely long, is generally quite faint. This also means that the ${\pi }_{{\rm{E}},\perp }$ component is much more sensitive to long-term trends in the data. In the present case, for which ${\pi }_{{\rm{E}},\parallel }\simeq 0$, this means that the direction of the ground-based parallax vector is determined much more confidently than its magnitude.

The Spitzer light curves can also be affected by long-term trends in the data, which can affect the parallax measurement. In their analysis of 50 Spitzer events from 2015, Zhu et al. (2017) identified five with obvious trends in the data, and Koshimoto & Bennett (2019) identified 14 more. There is only one case for which the causes of such trends have been investigated: KMT-2018-BLG-0029 (Gould et al. 2020). In that case, bright nearby blends with poorly determined positions were found to be likely to have generated trends, as the Spitzer camera rotated during the season. Because the source was faint and not well magnified, the trends were about 30% of the total observed flux variations. Nevertheless, after the trends were removed, the amplitude of the parallax measurement only changed by 20% (about 2σ). Thus, it is important to both carefully evaluate and minimize the impact of potential Spitzer systematics.

Refsdal (1966) originally analyzed satellite parallaxes prior to the time (Gould 1992) that it was recognized that the ground-based light curve alone would have any parallax information. Hence, although not explicitly stated, his was in essence a satellite-"only" analysis. The ground-based parameters $({t}_{0,\oplus },{u}_{0,\oplus },{t}_{{\rm{E}},\oplus })$ were directly compared to the satellite parameters $({t}_{0,\mathrm{sat}},{u}_{0,\mathrm{sat}},{t}_{{\rm{E}},\mathrm{sat}})$ to produce the parallax measurement

$$\begin{eqnarray}\begin{array}{rcl}{{\boldsymbol{\pi }}}_{{\rm{E}}} & = & \displaystyle \frac{\mathrm{au}}{{D}_{\perp }}({\rm{\Delta }}\tau ,{\rm{\Delta }}{u}_{0});\qquad {\rm{\Delta }}\tau \equiv \displaystyle \frac{{t}_{0,\mathrm{sat}}-{t}_{0,\oplus }}{{t}_{{\rm{E}}}};\\ {\rm{\Delta }}{u}_{0} & \equiv & {u}_{0,\mathrm{sat}}-{u}_{0,\oplus },\end{array}\end{eqnarray} \tag{ 4 }$$

where D_⊥is the projected separation of the satellite from Earth and where it was implicitly assumed that the Einstein timescales were the same ${t}_{{\rm{E}}}={t}_{{\rm{E}},\oplus }={t}_{{\rm{E}},\mathrm{sat}}$. The implicit idea (as illustrated in Figure 1 of Gould 1994 and first realized in Figure 1 of Yee et al. 2015b) is that $({t}_{0,\mathrm{sat}},{u}_{0,\mathrm{sat}},{t}_{{\rm{E}},\mathrm{sat}})$ would be "observables" from the satellite, just as the corresponding quantities were from Earth. Note that Equation (4) has a fourfold degeneracy because u₀ is a signed quantity but only $| {u}_{0}|$ is determined directly from the light curve. See Figure 4 of Gould (2004) for the sign convention.

However, in real Spitzer microlensing events, the peak is very often not observed from space, primarily because there is a ∼3–10 day time delay between identifying the event and initiating satellite observations (Figure 1 from Udalski et al. 2015b). Hence, while Equation (4) remains formally valid, it may no longer express the parallax measurement in terms of "observables," because (t₀, u₀)_sat may not be separately determined.

Gould (2019) generalized Refsdal's satellite-"only" analysis to the case of satellite data streams that did not cover the peak. He showed that if the source flux in the satellite observations was known and the baseline flux was measured, then each satellite measurement at finite magnification yields an exactly circular degeneracy in the ${{\boldsymbol{\pi }}}_{{\rm{E}}}$ plane. In the presence of measurement errors, these circles become finite annuli. If these measurements cover the peak, then the corresponding circles intersect in exactly two places, which then reproduces the Refsdal (1966) fourfold degeneracy (two pairs, one each for $\pm {u}_{0,\oplus }$). See Figure 3 of Gould (2019). On the other hand, the osculating circles from a series of late-time measurements combine to form an extended arc. See Figure 1 of Gould (2019). Such arcs may yield exquisite 1D constraints on ${{\boldsymbol{\pi }}}_{{\rm{E}}}$ while still providing almost no constraint on its amplitude ${\pi }_{{\rm{E}}}$. See the second row of Figure 2 from Zang et al. (2020) for an extreme example. Nevertheless, as that example makes clear, the addition of exterior information about the direction of ${{\boldsymbol{\pi }}}_{{\rm{E}}}$ can then constrain ${\pi }_{{\rm{E}}}$ very well. The first case of such an arc appearing in a Spitzer-"only" analysis was OGLE-2018-BLG-0596 (Jung et al. 2019). OGLE-2017-BLG-0406 has a qualitatively similar arc-like degeneracy.

We note that if ${({t}_{0},{u}_{0},{t}_{{\rm{E}}})}_{\oplus }$ are considered as known exactly, then for each trial value of ${{\boldsymbol{\pi }}}_{{\rm{E}}}=({\pi }_{{\rm{E}},N},{\pi }_{{\rm{E}},E})$, the remaining two parameters ${({f}_{s},{f}_{b})}_{\mathrm{Spitzer}}$ can be calculated analytically. That is, there are $({N}_{\mathrm{Spitzer}}+1)$ linear equations for two unknowns, where N_Spitzer is the number of Spitzer measurements, $F({t}_{k})$. These are N_Spitzer equations for the measurements,

$$\begin{eqnarray}\begin{array}{rcl}{y}_{k} & = & \displaystyle \sum _{i\,=\,1}^{2}{a}_{i}{g}_{i,k}\pm {\sigma }_{k}\quad {y}_{k}\equiv F({t}_{k}),\\ a & \equiv & {\left({f}_{s},{f}_{b}\right)}_{\mathrm{Spitzer}};\quad {g}_{1,k}\equiv A({t}_{k}),\quad {g}_{2,k}\equiv 1,\end{array}\end{eqnarray} \tag{ 5 }$$

plus one for the flux constraint,

$$\begin{eqnarray}\begin{array}{rcl}{y}_{0} & = & \displaystyle \sum _{i\,=\,1}^{2}{a}_{i}{g}_{i,0}\pm {\sigma }_{0}\quad {y}_{0}\equiv {f}_{{\rm{s}},\mathrm{spitzer},\mathrm{constr}},\\ {g}_{\mathrm{1,0}} & \equiv & 1\quad {g}_{2,k}\equiv 0.\end{array}\end{eqnarray} \tag{ 6 }$$

Then one solves in the usual way,

$$\begin{eqnarray}&&\begin{array}{l}{d}_{i}=\displaystyle \sum _{\mu =0}^{{N}_{\mathrm{Spitzer}}}\displaystyle \frac{{y}_{\mu }{g}_{i,\mu }}{{\sigma }_{\mu }^{2}};\qquad {b}_{i,j}=\displaystyle \sum _{\mu =0}^{{N}_{\mathrm{Spitzer}}}\displaystyle \frac{{g}_{i,\mu }{g}_{j,\mu }}{{\sigma }_{\mu }^{2}};\\ \,c\,=\,{b}^{-1}\qquad {a}_{i}=\displaystyle \sum _{j}{c}_{i,j}{d}_{j},\end{array}\end{eqnarray} \tag{ 7 }$$

with ${c}_{i,j}$ being the covariance matrix of the two parameters.

To evaluate the Spitzer-"only" parallax contours, we calculate ${A}_{\mathrm{Spitzer}}({t}_{k})$ by fixing ${({t}_{0},{u}_{0},{t}_{{\rm{E}}})}_{\oplus }$ according to the W+ and W− solutions shown in Table 3 and by fixing ${{\boldsymbol{\pi }}}_{{\rm{E}}}=({\pi }_{{\rm{E}},N},{\pi }_{{\rm{E}},E})$ at a grid of values. In Section 6, we evaluate ${f}_{{\rm{s}},\mathrm{spitzer},\mathrm{constr}}=11.10\pm 0.15$. We find that the Spitzer errors must be renormalized by a factor 3.4 to achieve ${\chi }^{2}/\mathrm{dof}=1$. The arc in Figure 2 shows the resulting Spitzer-"only" contours for the W+ solution. The diagonal contours represent the ground-only parallax measurement, which we have extended out to seven sigma analytically using the covariance matrix from the MCMC. Figure 3 shows the corresponding structures for the W- solution.

The most important feature is that the 1σ contours from the two parallax measurements overlap. Hence, there is no tension at all between the two determinations. Second, the direction of ${{\boldsymbol{\pi }}}_{{\rm{E}}}$ is essentially determined by the ground-based measurement. That is, even if the arc were displaced to the East or West, it would intersect the ground contours at a very similar polar angle. The only exception would be if it intersected very close to the origin. Third, the best-fit ground-based value of ${\pi }_{{\rm{E}},\perp }$ plays only a very small role in the point of overlap of these two sets of contours, which is shown in the right hand panel of the figure. That is, even if ${\pi }_{{\rm{E}},\perp }$ were displaced two sigma toward higher values, the overlap would occur in the same place. This means that the aspect of the ground-based data that is most vulnerable to systematic errors does not play much of a role in the final solution. The panel at the right shows that despite the fact that the ground-only and Spitzer-"only" measurements are effectively 1D, they combine to form tight 2D constraints.

We thus proceed to directly analyze the ground-based and Spitzer data jointly. The resulting microlensing-parameter estimates are given in Table 4, where in particular, we show two different representations of the parallax vector ${{\boldsymbol{\pi }}}_{{\rm{E}}}$—that is, in Cartesian $({\pi }_{{\rm{E}},N},{\pi }_{{\rm{E}},E})$ and polar $({\pi }_{{\rm{E}}},{\pi }_{\phi })$ coordinates. We evaluate the ${{\boldsymbol{\pi }}}_{{\rm{E}}}$ covariance matrix and use this to generate 1σ, 2σ, and 3σ contours, which are shown in the right panels Figures 2 and 3 as white ellipses. These show that the semi-analytic approach described in Section 5.1 and displayed in these figures works quite well, although not perfectly. This good agreement confirms that there is strong physical basis for the arguments given in that section.

Table 4.  Wide Models for Ground+Spitzer Data

Parameters	Wide $(+,+)$	Wide $(-,+)$
${\chi }^{2}/\mathrm{dof}$	29297.755/29310	29295.132/29310
t0 $({\mathrm{HJD}}^{{\prime} })$	7908.813 ± 0.001	7908.813 ± 0.001
u0 $({10}^{-3})$	9.281 ± 0.028	−9.281 ± 0.028
${t}_{{\rm{E}}}$ $(\mathrm{days})$	37.134 ± 0.083	37.133 ± 0.085
s	1.128 ± 0.001	1.128 ± 0.001
q $({10}^{-4})$	6.955 ± 0.061	6.970 ± 0.090
α $(\mathrm{rad})$	0.993 ± 0.001	−0.993 ± 0.001
ρ $({10}^{-3})$	5.852 ± 0.025	5.843 ± 0.025
${\pi }_{{\rm{E}},{\text{}}N}$	0.126(0.111) ± 0.021	0.120(0.113) ± 0.024
${\pi }_{{\rm{E}},{\text{}}E}$	0.062(0.066) ± 0.007	0.065(0.067) ± 0.007
${\pi }_{{\rm{E}}}$	0.140(0.130) ± 0.016	0.136(0.133) ± 0.018
${\phi }_{\pi }$	0.455(0.549) ± 0.127	0.499(0.549) ± 0.134
${f}_{S}(\mathrm{OGLE})$	1.459 ± 0.004	1.459 ± 0.004
${f}_{B}(\mathrm{OGLE})$	0.106 ± 0.004	0.105 ± 0.004
fS(Spitzer)	11.249 ± 0.164	11.210 ± 0.180
fB(Spitzer)	−2.656 ± 0.165	−2.614 ± 0.182
${t}_{\mathrm{ast}}$ $(\mathrm{days})$	0.217 ± 0.001	0.217 ± 0.001

Note. Mean values from the MCMC are shown in parentheses. All other values are from the best-fit model. ${\pi }_{{\rm{E}}}$, ${\phi }_{\pi }$, and ${t}_{\mathrm{ast}}$ are derived quantities and are not fitted independently. All fluxes are on an 18th mag scale (e.g., ${I}_{s}=18-2.5\,\mathrm{log}({f}_{s})$).

Download table as:  ASCIITypeset image

We derive the source magnitudes in the V and I bands by converting the instrumental source magnitude in MOA-Red and MOA-V bands into the standard Kron–Cousin I-band and Johnson V-band scales using the following relations:

$$\begin{eqnarray}\begin{array}{rcl}{I}_{\mathrm{OGLE} \mbox{-} \mathrm{III}}-{R}_{\mathrm{MOA}} & = & (28.132\pm 0.002)\\ & & \ -\ (0.206\pm 0.001){\left(V-R\right)}_{\mathrm{MOA}},\end{array}\end{eqnarray} \tag{ 9 }$$

$$\begin{eqnarray}\begin{array}{rcl}{V}_{\mathrm{OGLE} \mbox{-} \mathrm{III}}-{V}_{\mathrm{MOA}} & = & (28.302\pm 0.002)\\ & & \ -\ (0.108\pm 0.001){\left(V-R\right)}_{\mathrm{MOA}}.\end{array}\end{eqnarray} \tag{ 10 }$$

From the light-curve fitting using these formulae, we obtain the source color and magnitude ${(V-I)}_{{\rm{S}}}=2.581\pm 0.016$ and ${I}_{{\rm{S}}}\,=17.603\pm 0.011$. We also calibrate the CTIO H-band magnitude to 2MASS Carpenter (2001) scale with the following relation,

$$\begin{eqnarray}&&{H}_{2\mathrm{mass}}={H}_{\mathrm{CTIO}}-3.917\pm 0.009,\end{eqnarray} \tag{ 11 }$$

based on the stars within 120'' of the target. We find the source magnitude H_S = 14.696 ± 0.010 and derive color ${(V-H)}_{{\rm{S}}}\,=5.488\pm 0.016$ and ${(I-H)}_{{\rm{S}}}=2.907\pm 0.015$.

To obtain the intrinsic source color and magnitude, we use the red clump giants (RCG) centroid in the color–magnitude diagram (CMD) as a standard candle. Figures 4–6 show CMDs of stars within 120'' of the target. The V and I magnitudes are from OGLE-III catalog, and the H magnitude is from the VVV catalog, which is calibrated to the 2MASS scale, respectively. We find that the centroids of the RCGs in this field, which are indicated as filled red circles, are at ${I}_{\mathrm{RCG}}=16.302\pm 0.045$, ${(V-I)}_{\mathrm{RCG}}=2.623\pm 0.012$, ${(V-H)}_{\mathrm{RCG}}=5.517\pm 0.030$, and ${(I-H)}_{\mathrm{RCG}}=2.886\pm 0.016$ from these CMDs. From Nataf et al. (2016) and Bensy et al. (2013), we also find that the intrinsic magnitude and color of RCG should be ${I}_{\mathrm{RCG},0}=14.426\pm 0.040$, ${(V-I)}_{\mathrm{RCG},0}=1.060\pm 0.060$, ${(V-H)}_{\mathrm{RCG},0}=2.360\pm 0.090$, and ${(I-H)}_{\mathrm{RCG},0}=1.300\,\pm 0.060$. The color and magnitude of source and the centroid of RCG are summarized in Table 5. By subtracting the intrinsic RGC color and magnitude from the measured RGC positions in our CMDs, we find an extinction value of ${A}_{I,\mathrm{obs}}=1.876\,\pm 0.060$ and color excess values of $E{(V-I)}_{\mathrm{obs}}=1.563\,\pm 0.061$, $E{(V-H)}_{\mathrm{obs}}=3.157\pm 0.095$, and $E{(I-H)}_{\mathrm{obs}}\,=1.586\pm 0.062$.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

The extinction can be determined most accurately if three colors are used (Bennett et al. 2010). Following Bennett et al. (2010) and Koshimoto et al. (2017), we fit them with the extinction law of Cardelli et al. (1989) and Nishiyama et al. (2008, 2009). Table 6 shows the results of fitting extinction values to those of extinction laws. We adopt the ${R}_{{JKVI}}\equiv E(J-{Ks})/E(V-I)=0.3347$ value from Nataf et al. (2013) for the event coordinates. We see that the ${\chi }^{2}$ value using Nishiyama et al. (2008) extinction law is the smallest, and the extinction values agree with our measurement from our CMDs. Thus, we decide to use the results from Nishiyama et al. (2008) extinction law for the rest of the analysis.

Table 6.  Comparison of the Extinction Based on Different Extinction Laws

Extinction law	None	Cardelli et al. (1989)	Nishiyama et al. (2009)	Nishiyama et al. (2008)
AV	3.437 ± 0.086	3.565 ± 0.055	3.497 ± 0.062	${\bf{3.472}}\pm {\bf{0.082}}$
AI	1.876 ± 0.060	1.982 ± 0.050	1.931 ± 0.050	${\bf{1.911}}\pm {\bf{0.066}}$
AH	0.364 ± 0.103	0.583 ± 0.018	0.467 ± 0.012	${\bf{0.358}}\pm {\bf{0.009}}$
$E(V-I)$	1.563 ± 0.061	1.587 ± 0.037	1.566 ± 0.038	${\bf{1.561}}\pm {\bf{0.053}}$
$E(V-H)$	3.157 ± 0.095	2.987 ± 0.047	3.031 ± 0.056	${\bf{3.115}}\pm {\bf{0.074}}$
$E(I-H)$	1.586 ± 0.062	1.401 ± 0.033	1.464 ± 0.052	${\bf{1.554}}\pm {\bf{0.061}}$
${\chi }^{2}/\mathrm{dof}$	⋯	11.60/1	2.70/1	2.66/2

Note. The bold values are the values used for the analysis.

Download table as:  ASCIITypeset image

The extinction-corrected magnitude and color of the source indicate that it sits about 1.27 mag below the red clump centroid on the giant branch. A comparison to isochrones following Bennett et al. (2018a, 2018b) indicates that that source star is located on the giant branch in the Galactic bulge. Stars of similar color and magnitude that reside in the foreground or background have a negligible probability to be lensed because of an extremely low number density. So, we conclude the the source star almost certainly resides in the Galactic bulge.

Because the most precise determination comes from the $(V-H)$ and H relation (Bennett et al. 2015), we use the following relation to estimate ${\theta }_{\star }$,

$$\begin{eqnarray}&&\mathrm{log}{\theta }_{\mathrm{LD}}=0.536654\,+\,0.072703{\left(V-H\right)}_{{\rm{S}},0}-0.2{H}_{{\rm{S}},0},\end{eqnarray} \tag{ 12 }$$

where ${\theta }_{\mathrm{LD}}$ is the limb-darkened stellar angular diameter (Boyajian et al. 2014). This relation comes from a private communication with Boyajian by Bennett et al. (2015). For the best-fit parameter, we get ${\theta }_{\star }={\theta }_{\mathrm{LD}}/2=3.472\pm 0.085$ μas.

We also derive ${\theta }_{\star }$ using relation between ${(V-{K}_{{\rm{S}}})}_{{\rm{S}},0}$ and ${K}_{{\rm{S}},{\rm{S}},0}$ obtained from IRSF data. From the light-curve fitting, we get ${(V-{K}_{{\rm{S}}},{K}_{{\rm{S}}})}_{{\rm{S}}}=(5.262,14.923)\pm (0.091,0.093)$. From the results of Nishiyama et al. (2008), we also get the extinction in K_S-band ${A}_{{{\rm{K}}}_{{\rm{S}}}}=0.222\pm 0.005$ and color excess $E(V-{K}_{{\rm{S}}})=3.250\pm 0.077$. Thus we find ${(V-{K}_{{\rm{S}}},{K}_{{\rm{S}}})}_{{\rm{S}},0}\,=(2.011,14.701)\pm (0.122,0.090)$. To estimate ${\theta }_{\star }$, we use the following equation from Kervella et al. (2004):

$$\begin{eqnarray}&&\mathrm{log}{\theta }_{\mathrm{LD}}=0.5170\,+\,0.0755{\left(V-K\right)}_{{\rm{S}},0}-0.2{K}_{{\rm{S}},0}.\end{eqnarray} \tag{ 13 }$$

This gives θ_⋆ = 2.68 ± 0.14 μas, which is inconsistent with the one from ${(V-H,H)}_{S,0}$. We also get ${H}_{{\rm{S}}}=15.173\,\pm 0.090$ from light-curve fitting of IRSF data, which is about 0.5 mag fainter than the one we get from CTIO data. This is likely because we only have three observations from IRSF for this event, and our normal procedure for renormalizing error bars is not very reliable. Therefore, we adopt a θ_⋆ value derived from the CTIO V − H relations for the rest of the analysis.

We construct an IHL color–color diagram by matching field stars from OGLE-IV, VVV, and our own Spitzer photometry. We restrict attention to stars in the neighborhood of the clump, $(2.75\lt (I-H)\lt 3.10)\times (16\lt I\lt 17.6)$, and show the cross matches is Figure 7. We fit these points to a straight line and find $(I-L)=1.289[(I-H)-2.90]+2.215\pm 0.008$. We find from regression ${(I-{H}_{\mathrm{CT}13})}_{s}=1.109\pm 0.004$, and so ${(I-{H}_{\mathrm{VVV}})}_{s}=2.898\pm 0.010$. Hence this error in ${(I-H)}_{s}$ propagates to an error of 0.013 mag in ${(I-L)}_{s}$. To this, we must add in quadrature the error in the relation at the color of the source (0.01 mag), yielding finally $(I-L)=2.215\,\pm 0.015$.

Zoom In Zoom Out Reset image size

This approach implicitly assumes that the ∼0.1 mag scatter seen in Figure 7 is overwhelmingly due to measurement error rather than intrinsic variation. This is justified by the Bessell & Brett (1988) study of color–color relations based on bright isolated stars with excellent photometry, which found very small scatter.

However, this seemingly clear picture appears to be contradicted by the Gaia source proper motion

$$\begin{eqnarray}&&{{\boldsymbol{\mu }}}_{s}(N,E)=(0.105,0.124)\pm (0.752,0.840)\qquad (\mathrm{Gaia}),\end{eqnarray} \tag{ 14 }$$

that is, moving synchronously with the flat disk-rotation curve, rather than the mean motion of the bulge.

The Gaia measurement is very difficult to understand within the context of the microlensing solution. It would imply that the lens is moving relative to the source at ${v}_{\mathrm{rel}}\simeq {\mu }_{\mathrm{rel}}{D}_{{\rm{L}}}\,=135\,\mathrm{km}\,{{\rm{s}}}^{-1}({D}_{{\rm{L}}}/5\,\mathrm{kpc})$ in the prograde direction. While not impossible, this would be a very rare star. Another alternative to consider is that ${\pi }_{\mathrm{rel}}$ is actually somewhat smaller (due to measurement errors of ${\theta }_{{\rm{E}}}$ and ${\pi }_{{\rm{E}}}$) so that the lens could be in the bulge. However, the implied motion of the lens (12 $\mathrm{mas}\,{\mathrm{yr}}^{-1}$ relative to the mean motion of the bulge) would be extremely rare ${ \mathcal O }({10}^{-4})$ for a bulge star. Thus, the Gaia proper-motion measurement of the source would imply that the otherwise quite expected microlensing parameters were either incorrect or had extremely unusual implications.

This is one of two lines of argument that led us to suspect that the Gaia measurement was actually incorrect. The second was that in the course of constructing a cleaned Gaia proper-motion diagram of neighboring clump stars, we noticed that stars with parallax/error ratios $\pi /\sigma (\pi )\lt -2$ were preferentially extreme proper-motion outliers. That is, although the proper motions of the majority of such stars were distributed similarly to those of stars with more typical parallaxes, about 10% had proper-motion vectors near the edges or even outside the normal distribution and so were most likely to be the result of catastrophic errors. The Gaia parallax for the source star is $\pi =-0.96\pm 0.42\,\mathrm{mas}$. Thus, based on our small statistical study, and even without any external reason to suspect the measurement, the strong negative parallax implied a ∼10% probability of a catastrophic error. We also note that this star has an "astrometric excess noise sig" of 3.19. However, we show below that this is actually substantially below the median of a well-behaved "clean clump and near-clump sample." So this value is not, in itself, a reason to be suspicious of this star.

There is a long history of OGLE proper measurements of bulge sources dating back to the Sumi et al. (2004) catalog based on OGLE-II data. While there are no published catalogs based on the subsequent OGLE surveys, individual proper-motion measurements based on OGLE-IV are potentially more precise by a factor of several tens due to a five-times longer baseline and equal or higher cadence (Skowron et al. 2016b; Mróz et al. 2018; Chung et al. 2019; Shvartzvald et al. 2019). We apply this same technique to the OGLE-2017-BLG-0406 source and find, in the OGLE-IV reference frame tied to 1050 red clump stars within a $(6\buildrel{\,\prime}\over{.} 5\times 6\buildrel{\,\prime}\over{.} 5)$ square, ${{\boldsymbol{\mu }}}_{s,\mathrm{OGLE} \mbox{-} \mathrm{IV}}(N,E)=(0.923,-3.147)\,\pm (0.163,0.182)\mathrm{mas}\,{\mathrm{yr}}^{-1}$, where the errors are derived by assuming that errors of the individual position measurements are equal to the rms scatter about the best-fit straight line (i.e., $\sigma (N,E)=(10,11)\mathrm{mas}$), which corresponds to about 0.04 OGLE pixels. Figure 8 shows the 324 data points during the period 2010–2019 that went into this measurement.

Zoom In Zoom Out Reset image size

We then align the local OGLE-IV proper-motion frame to the Gaia frame by cross matching common stars. For this purpose, we consider Gaia stars within ${\rm{\Delta }}\theta \lt 3^{\prime}$ and with "astrometric excess noise sig" < 10 and then further restrict to our "clean clump and near-clump sample," which is defined by 16 < G < 18, $2\lt ({B}_{P}-{R}_{P})\lt 3$, $\sigma ({\mu }_{{\rm{R}}.{\rm{A}}.})\lt 0.6\,\mathrm{mas}\,{\mathrm{yr}}^{-1}$, $\sigma ({\mu }_{\mathrm{Decl}.})\lt 0.6\,\mathrm{mas}\,{\mathrm{yr}}^{-1}$, $\pi /\sigma (\pi )\gt -2$, and $\pi \lt 1\,\mathrm{mas}$. For purposes of finding the offset between two proper-motion frames, there is no reason to restrict to clump stars. However, the clump (and near-clump) sample allows us to identify and reject several data classes that are prone to catastrophic errors. We find ${\rm{\Delta }}{\boldsymbol{\mu }}(N,E)={{\boldsymbol{\mu }}}_{\mathrm{Gaia}}-{{\boldsymbol{\mu }}}_{\mathrm{OGLE} \mbox{-} \mathrm{IV}}=(-5.552,-3.391)\,\pm (0.042,0.052)\mathrm{mas}\,{\mathrm{yr}}^{-1}$, based on an initial set of 394 stars from which we eliminate nine and six three-sigma outliers, respectively. Hence, we obtain ${{\boldsymbol{\mu }}}_{{\rm{s}},\mathrm{Gaia}}={{\boldsymbol{\mu }}}_{s,\mathrm{OGLE} \mbox{-} \mathrm{IV}}+{\rm{\Delta }}{\boldsymbol{\mu }}\,=(-4.63,-6.54)\pm (0.17,0.19)$.

While these small formal errors accurately reflect the OGLE-IV measurement of the "catalog star" associated with the microlensed source, this catalog star is composed of both the source and a very small amount of blended light. Subtracting the precisely determined source flux from the somewhat more uncertain baseline flux of the catalog star, this blended flux is about 7% of the total. The true number could be slightly more or less. To take account of the possibly different proper motion of the blend, we augment the error in the source proper motion to a somewhat conservative $0.4\,\mathrm{mas}\,{\mathrm{yr}}^{-1}$,

$$\begin{eqnarray}\begin{array}{rcl}{{\boldsymbol{\mu }}}_{s}(N,E) & = & (-4.63,-6.54)\pm (0.40,0.40).\\ & & (\mathrm{OGLE} \mbox{-} \mathrm{IV}).\end{array}\end{eqnarray} \tag{ 15 }$$

Note that Equations (14) and (15) differ by about $8.1\,\mathrm{mas}\,{\mathrm{yr}}^{-1}$ or about 10σ using the reported Gaia uncertainties.

Our threshold of "astrometric excess noise sig" may appear at first site to be too generous. However, we find that in our final sample of 394 OGLE-Gaia matches, a fraction (6,15,30,48)% lie below (1,2,3,4), respectively, with a median of 4.1. Yet, the sample as whole has well-behaved proper motions, with only 1%–2% three-sigma outliers relative to OGLE.

To find the offset ${\rm{\Delta }}{\boldsymbol{\mu }}$ between the Gaia and OGLE-IV systems, we fit the proper-motion differences to a quadratic function of position centered at the lensed-source position. Because the formal Gaia errors were several times larger than the formal OGLE-IV errors, we considered only the former, and we rescaled these errors to enforce χ²/dof = 1. This yielded rescaling factors of 2.22 and 2.14 in the north and east directions, respectively. Figure 9 shows the proper-motion offsets as a function of each Equatorial coordinate. This figure shows some large-scale structure, which is removed by the quadratic fits, as well as some small-scale structure, which is not. However, this small-scale structure is relatively isolated and has a amplitude of a few tenths $\mathrm{mas}\,{\mathrm{yr}}^{-1}$, so it is unlikely to account for the increased scatter, which is of order $1\,\mathrm{mas}\,{\mathrm{yr}}^{-1}$. Rather, the most likely source of the majority of this additional scatter is underestimation of Gaia errors, which is exactly what is corrected by our error-renormalization procedure. To further explore this idea, for each star in our "clean clump and near-clump sample" (but now re-including the stars with π/σ(π) < −2), we calculate a parallax offset parameter η = (π − π₀)/σ(π), where π₀ = π_bulge − π_zpt = 70 μas, and we adopt ${\pi }_{\mathrm{bulge}}=120\,\mu \mathrm{as}$ for the mean parallax of the clump and ${\pi }_{\mathrm{zpt}}=50\,\mu \mathrm{as}$ for zero-point offset of the Gaia parallax system. After restricting attention to $| \eta | \lt 4$, we find $\langle \eta \rangle =-0.43$ (compared to zero expected), $\sigma (\eta )=1.31$ (compared to unity expected), and $\sqrt{\langle {\eta }^{2}\rangle }=1.38$ (compared to unity expected). If the error properties of the proper motions were similar to those of the parallaxes (as would be expected), then these numbers would partially explain the higher-than-expected scatter in the Gaia-OGLE-IV comparison.

Zoom In Zoom Out Reset image size

One possible source of this Gaia astrometry error is blending in the crowded Galactic bulge field. Gaia has an asymmetric PSF that can lead to blending with another star at a separation of ∼015 in some passes and not others. Such a circumstance would likely invalidate the Gaia astrometry, which could lead to negative parallaxes and proper-motion errors.

In order to derive statistically robust conclusions about planets from a given microlensing sample, the events must enter the sample without regard to whether they have planets or not.⁶³ For the Spitzer sample, this criterion gives rise to two distinct issues: (1) the events should be chosen for observations and assigned an observational cadence without regard to the presence of planets, and (2) the data-quality threshold for entering the sample should be the same for events with and without planets.

Regarding the first, Yee et al. (2015a) gave detailed prescriptions for including events under various modes of selection. However, from the present perspective the situation is relatively simple: OGLE-2017-BLG-0406 met so-called objective criteria and thus had to be observed, regardless of whether it had a planet or not. Moreover, it was observed at an "objectively determined" cadence. The only exception to this was that, as with essentially all known planetary events, OGLE-2017-BLG-0406 was observed at baseline during the 2019 season. The main motivation for this was to test for systematics, in part due to concerns raised by Koshimoto & Bennett (2019). See, for example, Gould et al. (2020). The addition of baseline data leads to a more precise parallax measurement. Thus, while these additional data are not in themselves relevant to the present point, they are to the next one.

Second, Zhu et al. (2017) established the following data-quality condition for the statistical study of the Galactic distribution of planets: the parallax should be adequately measured, meaning that the event should only be included in the sample provided that the error in "${D}_{8.3}$" satisfies

$$\begin{eqnarray}&&\sigma ({D}_{8.3})\lt 1.4\,\mathrm{kpc};\qquad {D}_{8.3}\equiv \displaystyle \frac{\mathrm{kpc}}{{\pi }_{\mathrm{rel}}/\mathrm{mas}+1/8.3},\end{eqnarray} \tag{ 19 }$$

where ${\pi }_{\mathrm{rel}}={\theta }_{{\rm{E}}}{\pi }_{{\rm{E}}}$. However, in order that this criterion be independent of the presence of the planet, they require that the estimate of $\sigma ({D}_{8.3})$ be derived from the corresponding single-lens event (with planet removed), rather than the actual event, which has added information from the planetary anomaly and (possibly) finite-source effects.

Therefore, we tested whether this event meets this criterion as follows. First, we make the analogous data set as described in Ryu et al. (2017). Next, we fit the data set with a single-lens model with parallax and finite-source effects—that is, six microlensing parameters $({t}_{o},{u}_{0},{t}_{{\rm{E}}},\rho ,{\pi }_{{\rm{E}},N},{\pi }_{{\rm{E}},E})$. Note that for this purpose we remove the 2019 Spitzer data, because these would not have been obtained if there had been no planet.

In typical cases of single-lens events (whether real or, as in this case, simulated), one does not measure ρ but only obtains some (usually weak) limit ${z}_{0}\gg 1$, where ${z}_{0}\equiv {u}_{0}/\rho$. Thus, one must estimate ${D}_{8.3}$ using a Bayesian analysis (Zhu et al. 2017). In the present case, ${z}_{0}=1.59$. Because ${z}_{0}\gt 1$, there is no caustic crossing in the single-lens event, but there is significant excess magnification at peak relative to the point-source case, which can be evaluated in the quadrupole approximation (Gould 2008) as

$$\begin{eqnarray}&&\displaystyle \frac{\delta A}{A}=\displaystyle \frac{1-{\rm{\Gamma }}/5}{8{z}_{0}^{2}}\to 4.5 \% .\end{eqnarray} \tag{ 20 }$$

Here we have adopted ${\rm{\Gamma }}=0.5$ as an illustrative value of the limb-darkening parameter. Therefore, given the high density and precision of the data over the peak, as well as over most of the event, we expect a very good measurement of ρ. In fact, we find that the single-lens light curve yields excellent constraints on both ${{\boldsymbol{\pi }}}_{{\rm{E}}}$ and ρ, with $\sigma ({D}_{8.3})=0.19\,\mathrm{kpc}$ (compared to $0.26\,\mathrm{kpc}$ for the actual event). Therefore, in this case, it is not necessary to conduct additional Bayesian analysis because the single-lens events satisfies the Zhu et al. (2017) criterion without it.

Hence, OGLE-2017-BLG-0406Lb becomes the eighth planet in the Spitzer-statistical sample, the others being OGLE-2014-BLG-0124Lb (Udalski et al. 2015b) OGLE-2015-BLG-0966Lb (Street et al. 2016), OGLE-2016-BLG-1190Lb (Ryu et al. 2017), OGLE-2016-BLG-1195Lb (Bond et al. 2017; Shvartzvald et al. 2017), OGLE-2017-BLG-1140Lb (Calchi Novati et al. 2018), OGLE-2018-BLG-0799Lb (W. Zang et al. 2020, in preparation), and KMT-2018-BLG-0029Lb (Gould et al. 2020). In addition, there are two microlensing planets from the Spitzer bulge survey that do not enter the statistical sample, OGLE-2016-BLG-1067Lb (Calchi Novati et al. 2019) and OGLE-2018-BLG-0596Lb (Jung et al. 2019), as well as one other Spitzer microlensing planet in the Galactic disk, Kojima-1b (Nucita et al. 2018; Fukui et al. 2019; Zang et al. 2020). To our knowledge, there are two other potential Spitzer-statistical-sample planets under active investigation. The Spitzer microlensing program ended in 2019.

Figures 2 and 3 show that the OGLE-2017-BLG-0406 parallax measurement derives from the intersection of two sets of 1D parallax contours—one from the ground-only measurement and the other from the Spitzer-"only" measurement. Gould (1999) first suggested the idea of combining 1D parallax information from Spitzer with 1D information from the ground, but after Spitzer observations of ∼1000 microlensing events, this is only the second case for which the intersection of such 1D information has been demonstrated.

However, this lack of identified cases may simply reflect the fact that OGLE-2017-BLG-0406 is only the fourth microlensing event for which Spitzer-"only" and ground-only parallax contours have been shown separately.⁶⁴ In two of the previous cases, KMT-2018-BLG-0029 (Gould et al. 2020) and OGLE-2018-BLG-0799 (W. Zang et al. 2020, in preparation) ${{\boldsymbol{\pi }}}_{{\rm{E}}}$ was basically determined by Spitzer-"only," while the much weaker ground-only information served mainly to help distinguish among degenerate solutions. In the other case, Kojima-1 (Zang et al. 2020), the ground-only microlensing data also provided relatively weak constraints that mainly helped distinguish between degenerate solutions. However, in this case, there was very precise, purely 1D information from VLTI GRAVITY interferometry (Dong et al. 2019).

It would be of interest to determine whether there are other such cases, in part to determine whether (as for OGLE-2017-BLG-0406) the Spitzer-"only" and ground-only contours were consistent at the 1σ (or perhaps 2σ) level. This could provide important statistical information on the frequency of systematic errors in both types of data sets. We note that the analytic Equations (5)–(7) provide a fast route to mapping Spitzer-"only" contours out to arbitrarily large σ.

With its measured mass $M=0.56\pm 0.07\,{M}_{\odot }$ and distance ${D}_{{\rm{L}}}=5.2\pm 0.5\,\mathrm{kpc}$, the OGLE-2017-BLG-0406 host is likely to be ∼90 times fainter than the microlensed source in the H band, with a 2σ range of 31–210 times fainter. According to Table 7, the lens and source are separating at ${\mu }_{\mathrm{rel},{\rm{H}}}=6.1\,\mathrm{mas}\,{\mathrm{yr}}^{-1}$ (i.e., just slightly larger than the geocentric proper motion). This implies a separation of $\sim 49\,$ mas in 2025 and ∼73 mas in 2029. With current instrumentation, the Keck AO system can probably detect the lens in 2029, but with improved instrumentation (Wizinowich et al. 2019), excellent AO corrections may be possible in the H or J bands, allowing detection in 2025. With an ELT, it may be possible to detect it sooner. James Webb Space Telescope may be able to detect it earlier than 2025 via image elongation (Bennett et al. 2007) or the color-dependent centroid method (Bennett et al. 2006; Bhattacharya et al. 2019). Multi-orbit HST observations might be able to detect the lens by 2025, but the source and lens are much too faint for VLT GRAVITY.