Abstract
The abundance of short-period planetary systems with high orbital obliquities relative to the spin of their host stars is often taken as evidence that scattering processes play important roles in the formation and evolution of these systems. More recent studies have suggested that wide binary companions can tilt protoplanetary disks, inducing a high stellar obliquity that form through smooth processes like disk migration. DS Tuc Ab, a transiting planet with an 8.138 day period in the 40 Myr Tucana–Horologium association, likely orbits in the same plane as its now-dissipated protoplanetary disk, enabling us to test these theories of disk physics. Here, we report on Rossiter–McLaughlin observations of one transit of DS Tuc Ab with the Planet Finder Spectrograph on the Magellan Clay Telescope at Las Campanas Observatory. We confirm the previously detected planet by modeling the planet transit and stellar activity signals simultaneously. We test multiple models to describe the stellar activity-induced radial velocity variations over the night of the transit, finding the obliquity to be low: λ = 12° ± 13°, which suggests that this planet likely formed through smooth disk processes and its protoplanetary disk was not significantly torqued by DS Tuc B. The specific stellar activity model chosen affects the results at the ≈5° level. This is the youngest planet to be observed using this technique; we provide a discussion on best practices to accurately measure the observed signal of similar young planets.
1. Introduction
Each discovered planetary system represents an outcome of the planet formation process, and therefore provides an opportunity to learn about how different planets form in different environments. However, each observed present-day system is not a pure laboratory: over billions of years, planet–planet and planet–star gravitational interactions can scatter, torque, migrate, or otherwise perturb orbits, distancing planetary systems from their initial formation state (Kozai 1962; Lidov 1962; Fabrycky & Tremaine 2007; Chatterjee et al. 2008). This picture is complicated by the fact that, in many cases, stellar ages are very poorly known (e.g., Barnes 2007; Soderblom 2010). These factors make it challenging to develop and test models of planet formation that can explain all observations.
The origins of hot Jupiters are still unclear (Dawson & Johnson 2018). Kozai–Lidov cycles and tidal friction are often invoked to explain the formation of hot Jupiters (Fabrycky & Tremaine 2007), but smooth disk migration provides a reasonable alternative in many cases (Ida & Lin 2008). Multiple channels may be required to explain all of the observed systems: Nelson et al. (2017) analyze data from the HAT and WASP exoplanet surveys, and find the data can be well-fit by a model in which ∼85% of hot Jupiters are formed through high-eccentricity migration and ∼15% through disk migration.
A population of low-obliquity planets10 is often considered a signature of smooth disk migration (Morton & Johnson 2011; Ford 2014). However, Albrecht et al. (2012) show that obliquity is an imperfect tracer of the formation history for many stars, as the tidal realignment timescale for a massive, nearby planet can be shorter than the age of the system for many stars with convective outer layers. Batygin (2012) suggests wide binary companions or nearby stars in the birth cluster can torque disks to random inclinations over Myr timescales. In these cases, young planets in binary systems will have random obliquities even at ages of a few Myr, rather than these obliquities being excited by the companion over much slower timescales. Franchini et al. (2020) also highlight the possibility that a planet can be tilted out of the plane of the protoplanetary disk by a binary companion in only a few Myr.
Planets in young clusters are valuable resources to provide clean test cases for planet formation. Dynamical interactions like the Kozai–Lidov effect can, depending on the system architecture, occur over hundreds of millions or billions of years (Montet et al. 2015; Naoz 2016). For systems with younger ages, we can rule out many slow-timescale dynamical interactions, meaning it is likely that the orbit of the planet traces the orbit of the now-dissipated disk. With a statistical sample of the obliquities of young planets, we can test the hypothesis of Batygin (2012) to see if the torquing of a disk by a distant perturber is a common process. However, such a survey is limited by the small number of planetary systems around young stars. There are only a handful of transiting planets known to be younger than 100 Myr, identified by the host star's membership in young moving groups or star-forming regions (David et al. 2016; Mann et al. 2016; David et al. 2019).
Recently, Sector 1 data from the Transiting Exoplanet Survey Satellite (TESS, Ricker et al. 2014) were used to identify three transits of a planet with an orbital period of 8.14 days around the star DS Tuc A (Benatti et al. 2019; Newton et al. 2019). These papers statistically validated and characterized this planet, finding results broadly consistent with each other. Newton et al. (2019) find a planet radius of 5.70 ± 0.17 R and a transit duration of 0.1324 ± 0.0005 days, with the planet orbiting a G6V star with an effective temperature of 5430 ± 80 k, and a model-dependent radius of 0.964 ± 0.029. Benatti et al. (2019) similarly find a planet radius of 5.63 ± 0.22 R
and a transit duration of 0.1324 ± 0.0005 days, with the planet orbiting a G6V star with an effective temperature of 5430 ± 80 k, and a model-dependent radius of 0.964 ± 0.029. Benatti et al. (2019) similarly find a planet radius of 5.63 ± 0.22 R and a transit duration of 0.119 days, with the planet orbiting a G6V star with an effective temperature of 5542 ± 21 k, and a model-dependent radius of 0.872 ± 0.027 R
and a transit duration of 0.119 days, with the planet orbiting a G6V star with an effective temperature of 5542 ± 21 k, and a model-dependent radius of 0.872 ± 0.027 R . We refer the reader to those two papers for a detailed discussion of the stellar parameters and transit fits.
. We refer the reader to those two papers for a detailed discussion of the stellar parameters and transit fits.
DS Tuc is a member of the Tucana–Horologium (Tuc–Hor) association, which has an age of 35–45 Myr (Bell et al. 2015; Crundall et al. 2019). DS Tuc itself is a binary, with a K3V companion at a projected separation of 240 au. From Holman et al. (1997), the timescale for Kozai–Lidov interactions is
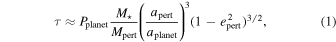
where Pplanet is the the orbital period of a planet with orbital semimajor axis aplanet about a host of mass M⋆, Mpert is the mass of the perturbing star, and apert and epert the semimajor axis and eccentricity of the outer object's orbit around the host star/planet system.
From the orbital parameters in Newton et al. (2019), M⋆/Mpert ≈ 1.2, apert/aplanet ≈ 2000, although the posterior distribution is highly skewed to larger values, and  , so the timescale τ from Equation (1) is more than 100 Myr, and possibly much longer depending on the true semimajor axis ratio.
, so the timescale τ from Equation (1) is more than 100 Myr, and possibly much longer depending on the true semimajor axis ratio.
As the age of the system is younger than this timescale, the planet likely has not had time to undergo these oscillations and is more likely to trace the orientation of the now-dissipated protoplanetary disk. Measuring the obliquity of the stellar spin relative to the orbit of the planet thus enables us to test theories of disk torquing. We can measure the projected obliquity between the spin of the star and the orbit of the planet through the Rossiter–McLaughlin (R–M) effect, in which an apparent redshift and blueshift in the radial velocity (RV) of the star are observed as a transiting planet occults the blueshifted and redshifted hemispheres of the rotating star, respectively (McLaughlin 1924; Rossiter 1924). DS Tuc Ab is the youngest known planet for which such an observation has been attempted, providing the best laboratory we have to test this theory. We note that Zhou et al. (2019) also obtained three transits of this planet, including two with the Planet Finder Spectrograph (PFS), for a complementary Doppler tomographic analysis of this system. These two works use different data sets and analysis techniques, providing independent checks of the methods and assumptions made in each work.
The rest of this paper is organized as follows. In Section 2, we describe the observations. In Section 3, we describe our data analysis. In Section 4, we present our results. In Section 5, we discuss best practices for future similar observations of young stars, as well as potential confounding factors and future work.
2. Observations
We obtained data with PFS on the Magellan Clay Telescope (Crane et al. 2006, 2008, 2010). On 2019 Aug 11 from UT 01:12 to UT 07:10, we obtained 49 RV measurements of DS Tuc A. The transit duration is 190 minutes, meaning approximately 50% of the data were obtained in transit while the other half provide information about the out-of-transit RV baseline. Each exposure was 360 s in length and was taken with the 0 3 × 2
3 × 2 5 slit, which provides a full-width at half maximum (FWHM) resolution of R ≈ 130,000 with five pixels per FWHM. All observations were taken with the iodine cell in place (Marcy & Butler 1992), which imprints a series of narrow lines at known wavelengths to measure the instrument point-spread function (PSF) and wavelength solution at each epoch.
5 slit, which provides a full-width at half maximum (FWHM) resolution of R ≈ 130,000 with five pixels per FWHM. All observations were taken with the iodine cell in place (Marcy & Butler 1992), which imprints a series of narrow lines at known wavelengths to measure the instrument point-spread function (PSF) and wavelength solution at each epoch.
From these spectra, we also derive two spectroscopic activity indicators: the emission flux measured in the Ca II H & K lines, SHK, and the emission in the Hα line, "SHα." Here, SHK is defined as in Duncan et al. (1991), with the updated R continuum area center from Santos et al. (2000), and SHα is defined as in Gomes da Silva et al. (2011).
To characterize the stellar activity–induced variations, we also obtained 12 additional out-of-transit observations of DS Tuc A. These included four observations over two nights on 2019 August 21 and 2019 August 22, and eight observations over four nights from 2019 September 11 to 2019 September 14 (all dates UT). These observations had exposure lengths varying from 360 to 600 s under variable sky conditions, with the goal of achieving a similar signal-to-noise ratio (S/N) in each of these spectra as during the night of the transit, as well as to provide us with the opportunity to measure the RV variability of the star on rotational period timescales.
We also collected a template spectrum of DS Tuc A on the night of the transit, immediately after the observations described above. This spectrum, obtained under similar conditions and with the same slit, but without the iodine cell in the light path, is used in the pipeline RV modeling. All observations were then analyzed using the standard PFS pipeline (Butler et al. 1996), which divides the spectrum into 2 Å chunks and fits each chunk independently. The resultant RV is the weighted mean of the RVs of each chunk, and the weighted variance across chunks provides an estimate of the uncertainty. We tested deriving RVs for DS Tuc A using all of the available data and using only data from the night of the transit, finding a lower point-to-point scatter with the latter strategy. This is likely due to changes in the line profile shape on rotational timescales as the stellar surface varies.
As the starspots and stellar activity levels change on the surface of the star, this affects the behavior of each 2 Å chunk. The weight of each chunk is calculated from the behavior of the RVs reported from this particular chunk across the data set. Chunks with more RV information are more likely, on average, to see a larger effect from these stellar activity changes, leading to these chunks being downweighted as more data are included, increasing the noise in the final output RVs.
As a result, we achieve the highest RV precision for the transit when we only consider data from the night of the transit itself, all collected at approximately the same levels of stellar activity. We thus use the results of two different extractions when considering the data from the night of the transit itself and from the later observations, which typically have approximately twice the RV uncertainty despite generally being observed with the same expected S/N. In practice, this strategy means that there may be a small RV offset between the two subsections of the data. In comparing the two reductions, we find an offset at the 15 m s−1 level, but as we only consider the data from the transit night itself when modeling the R–M signal, this should not affect our results.
The resultant RVs are given in Table 1 and displayed in Figure 1.
Figure 1. RV time series for (left) the observed transit and (right) a time span covering approximately one stellar rotation period, as inferred from TESS photometry and discussed in Section 5.4. Note the different vertical scalings on each subplot. The R–M signal is easily detectable, occurring over a timescale significantly different from that of the rotationally induced variability signal. The data from the night of the transit and continuing observations were analyzed in two separate data reductions, as described in Section 2.
Download figure:
Standard image High-resolution imageTable 1. Derived RVs for DS Tuc A
| Time | RV | Uncertainty | SHK | Hα |
|---|---|---|---|---|
| (BJD) | (m s−1) | (m s−1) | ||
| 2458706.55618 | −10.84 | 4.83 | 0.5826 | 0.05566 |
| 2458706.56101 | −14.13 | 4.14 | 0.5735 | 0.05596 |
| 2458706.56592 | −11.80 | 4.45 | 0.5679 | 0.05615 |
| 2458706.57080 | −23.17 | 4.59 | 0.5712 | 0.05566 |
| 2458706.57570 | −20.68 | 3.82 | 0.5727 | 0.05597 |
| 2458706.58047 | −24.58 | 4.33 | 0.5771 | 0.05603 |
| 2458706.58537 | −23.59 | 4.01 | 0.5737 | 0.05593 |
| 2458706.59023 | −26.70 | 4.58 | 0.5809 | 0.05613 |
| 2458706.59529 | −18.26 | 4.61 | 0.5849 | 0.05630 |
| 2458706.60010 | −17.40 | 4.56 | 0.5887 | 0.05648 |
| 2458706.60506 | −26.49 | 4.97 | 0.5993 | 0.05594 |
| 2458706.60996 | 9.87 | 4.96 | 0.5900 | 0.05670 |
| 2458706.61486 | 20.74 | 4.41 | 0.5936 | 0.05597 |
| 2458706.61966 | 12.43 | 4.68 | 0.5992 | 0.05641 |
| 2458706.62472 | 14.68 | 4.59 | 0.5853 | 0.05667 |
| 2458706.62965 | 22.34 | 4.90 | 0.6046 | 0.05718 |
| 2458706.63939 | 26.89 | 4.26 | 0.5839 | 0.05625 |
| 2458706.64420 | 26.72 | 4.79 | 0.5985 | 0.05671 |
| 2458706.65419 | 15.13 | 4.97 | 0.5898 | 0.05628 |
| 2458706.65893 | 8.84 | 3.88 | 0.5716 | 0.05611 |
| 2458706.66370 | 4.60 | 3.64 | 0.5712 | 0.05614 |
| 2458706.66866 | −4.96 | 4.21 | 0.5858 | 0.05610 |
| 2458706.67356 | −10.62 | 4.09 | 0.5781 | 0.05598 |
| 2458706.67856 | −21.84 | 3.79 | 0.5755 | 0.05600 |
| 2458706.68325 | −29.88 | 3.91 | 0.5752 | 0.05585 |
| 2458706.68844 | −45.36 | 4.55 | 0.5793 | 0.05599 |
| 2458706.69319 | −42.99 | 3.89 | 0.5684 | 0.05592 |
| 2458706.69809 | −32.38 | 4.02 | 0.5645 | 0.05529 |
| 2458706.70304 | −43.37 | 3.90 | 0.5606 | 0.05518 |
| 2458706.70783 | −35.81 | 3.98 | 0.5680 | 0.05540 |
| 2458706.71273 | −38.21 | 3.85 | 0.5670 | 0.05539 |
| 2458706.71765 | −46.83 | 3.91 | 0.5659 | 0.05522 |
| 2458706.72256 | −33.74 | 4.06 | 0.5646 | 0.05535 |
| 2458706.72746 | −26.33 | 4.21 | 0.5659 | 0.05535 |
| 2458706.73235 | 4.43 | 3.97 | 0.5588 | 0.05521 |
| 2458706.73731 | 9.93 | 3.52 | 0.5567 | 0.05513 |
| 2458706.74210 | 6.50 | 3.89 | 0.5596 | 0.05489 |
| 2458706.74700 | 8.13 | 3.74 | 0.5571 | 0.05511 |
| 2458706.75197 | 8.98 | 3.97 | 0.5574 | 0.05508 |
| 2458706.75683 | 23.30 | 4.15 | 0.5646 | 0.05516 |
| 2458706.76179 | 13.34 | 3.98 | 0.5647 | 0.05524 |
| 2458706.76657 | 12.16 | 4.56 | 0.5607 | 0.05499 |
| 2458706.77163 | 13.26 | 4.39 | 0.5632 | 0.05460 |
| 2458706.77643 | 13.52 | 4.49 | 0.5623 | 0.05483 |
| 2458706.78139 | 14.45 | 4.47 | 0.5607 | 0.05495 |
| 2458706.78620 | 25.45 | 4.27 | 0.5590 | 0.05460 |
| 2458706.79111 | 0.00 | 4.46 | 0.5577 | 0.05445 |
| 2458706.79602 | 34.67 | 4.21 | 0.5524 | 0.05464 |
| 2458706.80090 | 31.51 | 4.25 | 0.5585 | 0.05452 |
| 2458716.59155 | 100.30 | 5.84 | ⋯ | ⋯ |
| 2458716.72215 | 105.19 | 6.25 | ⋯ | ⋯ |
| 2458717.62611 | 146.51 | 8.11 | ⋯ | ⋯ |
| 2458717.77760 | −71.01 | 7.04 | ⋯ | ⋯ |
| 2458737.72011 | 199.55 | 8.73 | ⋯ | ⋯ |
| 2458737.80174 | 131.10 | 8.98 | ⋯ | ⋯ |
| 2458738.67055 | −76.18 | 7.18 | ⋯ | ⋯ |
| 2458738.76341 | −79.52 | 7.87 | ⋯ | ⋯ |
| 2458739.65311 | 67.24 | 7.91 | ⋯ | ⋯ |
| 2458739.77091 | 135.17 | 8.23 | ⋯ | ⋯ |
| 2458740.65811 | 66.63 | 7.77 | ⋯ | ⋯ |
| 2458740.75524 | 22.49 | 7.56 | ⋯ | ⋯ |
Download table as: ASCIITypeset image
3. Data Analysis
We model the inferred radial velocities with version 1.0.0.dev311 of the starry package of Luger et al. (2019). The starry package models the stellar surface brightness and velocity field as an expansion of spherical harmonics, under which light curve and RV computations are analytic. As the ability to model the R–M effect is currently only available in the development version of the code, we describe it briefly here.
The RV anomaly ΔRV due to the R–M may be expressed as (e.g., Giménez 2006)

where I(x, y) is the intensity at a point (x, y) on the projected disk of the star, v(x, y) is the RV at that point, and the integrals are taken over the visible portion of the projected disk. The radial component of the velocity field may be written in Cartesian coordinates as (e.g., Short et al. 2018)
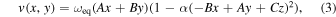
where  ,
,
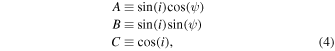
and i and ψ are the stellar inclination and obliquity, respectively. The constant α is the linear shear due to differential rotation, whose effect is to scale the rotational angular velocity of the star according to
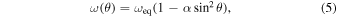
where  is the angular rotational velocity as a function of the latitude θ and ωeq is the angular velocity at the equator. The coordinate system adopted in Equation (3) is such that the x − y plane is the plane of the sky and
is the angular rotational velocity as a function of the latitude θ and ωeq is the angular velocity at the equator. The coordinate system adopted in Equation (3) is such that the x − y plane is the plane of the sky and  points toward the observer. The planet is assumed to transit the star along the
points toward the observer. The planet is assumed to transit the star along the  direction in a counterclockwise orbit about
direction in a counterclockwise orbit about  . The obliquity λ is therefore the component of the misalignment angle between the stellar rotation axis and the angular momentum vector of the planet projected onto the plane of the sky.
. The obliquity λ is therefore the component of the misalignment angle between the stellar rotation axis and the angular momentum vector of the planet projected onto the plane of the sky.
Because Equation (3) is a third-degree polynomial in x, y, and z, it may be expressed exactly as a spherical harmonic expansion of degree l = 3 (Luger et al. 2019). This is done by expanding the products in Equation (3) to obtain the coefficients multiplying each term in the polynomial basis (Equation (7) in Luger et al. 2019) and transforming them via the spherical harmonic change of basis matrix (Equation (9) in Luger et al. 2019).12
Under the assumption of quadratic limb darkening, the intensity field I(x, y) may also be expressed exactly as a spherical harmonic expansion of degree l = 2 (Luger et al. 2019). Since the product of two spherical harmonics is also a spherical harmonic, the integrand in Equation (2) may be expressed exactly as a degree l = 5 spherical harmonic expansion. We may therefore use the machinery in starry to analytically compute both integrals in Equation (2) when the star is occulted by a planet. Note that a similar approach was used by Bedell et al. (2019), who model the R–M effect of the hot Jupiter HD 189733b with starry.
Finally, in the sections that follow, we explore models in which the star has a single dark Gaussian-shaped spot. In starry, surface features such as spots are also modeled as an expansion of spherical harmonics up to a degree lmax. Again, since spherical harmonics are closed under multiplication, the intensity field I(x, y) of a quadratically limb-darkened spotted surface is simply a sum of spherical harmonics of degree lmax + 2. The total degree of the velocity-weighted intensity (the integrand in Equation (2)) is therefore lmax + 5.
3.1. Model
While the R–M signal model is always developed with starry in our analysis, we test multiple approaches to model the effects of the star on these observations. Over the six hours of the transit, the apparent RV of the star increases by more than 50 m s−1. In Section 5.2, we argue that this trend is due to stellar activity rather than an additional unseen planet. Regardless of the cause of this signal, in order to accurately measure the obliquity of the transiting planet, we must model the underlying stellar behavior as well. We test several different approaches to this problem, to ensure our results are not sensitive to our assumptions about the star. We use low-order polynomials, up to the third degree, to fit the relatively long-term variability during the night of the transit. Such low-order polynomials often provide a reasonable description of stellar activity on transit timescales, both in spectroscopic and photometric data (e.g., Sanchis-Ojeda et al. 2013; Neveu-VanMalle et al. 2016). We also build a stellar activity model by fitting a function that is a linear sum of the observed SHα and calcium SHK measurements during the night, which are correlated with the observed RV, as has been seen in previous analyses of spectroscopic observations of potential planet hosts (e.g., Robertson et al. 2015; Lanza et al. 2019). Finally, we also fit starry models of a single starspot in time. The dark spot is modeled as an lmax = 4 spherical harmonic expansion of a symmetric two-dimensional Gaussian flux decrement on the surface of the star; we allow the spot's size, contrast, and location to vary as we fit both signals.
For every model, we can then calculate the expected sum of the R–M signal and the stellar activity signal at each cadence, in order to compare to the data. This strategy allows us to understand, in a relative sense, how well each of the three models fit the data. It also gives us the opportunity to verify that the resultant obliquity measurement does not depend on the specific prescription of the stellar activity signal.
3.2. Likelihood Function
An accurate likelihood function is critical to ensuring an accurate measurement of the posterior distribution for each parameter. Each observation has an associated uncertainty, calculated as the weighted standard deviation of the calculated mean of each of the 2 Å chunks fit at each epoch. For this young and active star, this likelihood may not represent the true uncertainty in the measured RV at each epoch. For example, occultations of small spots across the surface of the star could cause the observed RV to vary from epoch to epoch, similar to how starspots can affect the observed transit depth in photometric monitoring (Sanchis-Ojeda et al. 2013). Additionally, stellar flares with characteristic timescales similar to a single exposure have been shown to induce RV variations at the 10–100 m s−1 level (Reiners 2009).
We test multiple likelihood functions with the same form. First, we assume each data point is drawn from a mixture model (e.g., McLachlan & Peel 2000) that is the sum of two Gaussian functions, each with a different variance:
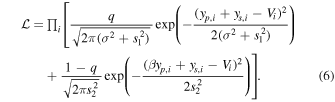
Under this model, the ith measurement Vi is compared to our model yi. The model is further subdivided into a contribution from the slowly varying background RV baseline due to the star,  and from the signal induced by the planet crossing the inhomogeneous surface of the star and blocking some fraction of the stellar disk,
and from the signal induced by the planet crossing the inhomogeneous surface of the star and blocking some fraction of the stellar disk,  . In the definition of this likelihood function, each data point has some probability q of being a "good" data point drawn from a relatively narrow distribution. This distribution is a combination of the PFS pipeline uncertainty, σ, and an additional jitter term, s1, added in quadrature. Each data point also has a probability
. In the definition of this likelihood function, each data point has some probability q of being a "good" data point drawn from a relatively narrow distribution. This distribution is a combination of the PFS pipeline uncertainty, σ, and an additional jitter term, s1, added in quadrature. Each data point also has a probability  of being drawn from a much broader distribution, with a separate jitter term, s2, to account for the possibility of stellar effects that significantly affect only a small number of data points. We allow the width of both Gaussian distributions to vary in our fitting procedure. Additionally, q is a free parameter: if the data were well-modeled by a single Gaussian, we would find the posterior distribution on q to be consistent with 1.0. Forcing q = 1 would thus fit the data using only a single Gaussian.
of being drawn from a much broader distribution, with a separate jitter term, s2, to account for the possibility of stellar effects that significantly affect only a small number of data points. We allow the width of both Gaussian distributions to vary in our fitting procedure. Additionally, q is a free parameter: if the data were well-modeled by a single Gaussian, we would find the posterior distribution on q to be consistent with 1.0. Forcing q = 1 would thus fit the data using only a single Gaussian.
These two Gaussians do not need to have the same mean. The surface of the star, as a rapidly rotating G dwarf, is likely dominated by dark starspots rather than bright faculae (Montet et al. 2017). Each dark spot will induce a signal with roughly the same shape as the R–M effect for an aligned system: as the spot occults the blueshifted hemisphere of the star, it will induce an apparent redshift and vice versa. As a planet occults a spot then, just as this phenomenon produces a brief brightening in a transit light curve (Désert et al. 2011; Sanchis-Ojeda et al. 2013; Morris et al. 2017), a spot-crossing event would cause a temporary decrease in the magnitude of the R–M signal. To allow for this effect in our fitting procedure, we allow for the broader Gaussian in our mixture model to be offset by some factor that is directly proportional to the magnitude of the R–M signal at that epoch. We parameterize this offset factor in Equation (6) as β.
When β = 1, the means of the two Gaussians overlap precisely, leaving us with a standard mixture model, as might be expected if the extra variability were not related to starspots. Again, β is fit as a free parameter, so if the data were well-modeled as a mixture model of two Gaussians with the same mean, we would find the posterior on β to be consistent with unity.
We only offset the broader Gaussian. Each starspot is unique, and each draw from our posterior tests only a single β value, although disparate starspots with different sizes and different contrast ratios will lead to a different amount of an expected shift from cadence to cadence. This uncertainty is manifested through the broader of the two Gaussian terms. Plainly, this model assumes q is the probability that an observation is not significantly affected by stellar activity. There is then a  probability that the observation is significantly affected by stellar activity, in which case the magnitude of the effects are relatively uncertain—but likely to skew the observation toward smaller absolute values by some factor β. We note that we also tested models where β applied to both Gaussian terms, but found this change did not significantly affect our results.
probability that the observation is significantly affected by stellar activity, in which case the magnitude of the effects are relatively uncertain—but likely to skew the observation toward smaller absolute values by some factor β. We note that we also tested models where β applied to both Gaussian terms, but found this change did not significantly affect our results.
3.3. Fitting
As described in Section 3.1, We test three different parameterizations to fit the long-term trend. We also test likelihood functions where β is fixed at 1.0 and models where q is fixed at 1.0 (in which case, β is undefined) for each parameterization, giving us nine tests total.
We apply a quadratic limb darkening model for the star, following the prescription of Kipping (2013). We use uniform priors in both parameters, subject to the constraints described in that paper, which enable uninformative sampling of both parameters. We do not fix our limb darkening to theoretical models, which have been shown to induce significant biases for transit observations of planets orbiting active, spotted stars (Csizmadia et al. 2013).
We fit these models to evaluate the posterior distribution using the emcee package of Foreman-Mackey et al. (2013), an implementation of the affine-invariant ensemble sampler of Goodman & Weare (2010). For all explorations using the cubic polynomial out-of-transit model, we initialize 500 walkers; for all other runs, we initialize 600 walkers. We run each for 3000 steps, removing the first 2000 as burn-in and considering the final 1000 steps in our final analysis. We verify that our chains have converged following the method of Geweke (1992) and through visual inspection.
Here, we assume the planet orbit is circular. Given only information about the transit, and assuming the orbital velocity of the planet does not change significantly during the transit, there is a degeneracy between the eccentricity and the stellar radius. We choose to force circular orbits and fit the orbital separation a/ as a free parameter. The opposite approach would be equally valid and produce similar results. We include uniform priors on all parameters except for the projected rotational velocity
as a free parameter. The opposite approach would be equally valid and produce similar results. We include uniform priors on all parameters except for the projected rotational velocity  and the radius ratio Rp/
and the radius ratio Rp/ . For both parameters, Benatti et al. (2019) and Newton et al. (2019) provide discrepant results; we conservatively apply Gaussian priors with means of 18.3 km s−1 and 0.057 and standard deviations of 1.8 km s−1 and 0.003 for
. For both parameters, Benatti et al. (2019) and Newton et al. (2019) provide discrepant results; we conservatively apply Gaussian priors with means of 18.3 km s−1 and 0.057 and standard deviations of 1.8 km s−1 and 0.003 for  and Rp/
and Rp/ , respectively. In the former case, the two projected rotational velocities are consistent with each other, but the uncertainty on the measurement from Newton et al. (2019) is an order of magnitude smaller than the one from Benatti et al. (2019). Here, we use the less precise measurement. For Rp/
, respectively. In the former case, the two projected rotational velocities are consistent with each other, but the uncertainty on the measurement from Newton et al. (2019) is an order of magnitude smaller than the one from Benatti et al. (2019). Here, we use the less precise measurement. For Rp/ , we choose a value midway between the two results, which have similar published uncertainties, with a width on our prior large enough to encompass both results at 1σ. We note that these two parameters both affect the amplitude of the R–M signal but not the asymmetry that signals a projected spin–orbit misalignment. An improper prior on one of these variables would then affect our inference of the other parameter, but would not have a significant effect on the measured obliquity. While these papers do predict times of transit and impact parameters, we apply uniform priors on each of these parameters as well, to allow for the possibility that dynamical interactions have affected the transit timing and impact parameter from the TESS epochs to the present day. When applying a spot model directly through starry, we apply uniform priors on the spot latitude, longitude, contrast ratio, and logarithm of the spot size.
, we choose a value midway between the two results, which have similar published uncertainties, with a width on our prior large enough to encompass both results at 1σ. We note that these two parameters both affect the amplitude of the R–M signal but not the asymmetry that signals a projected spin–orbit misalignment. An improper prior on one of these variables would then affect our inference of the other parameter, but would not have a significant effect on the measured obliquity. While these papers do predict times of transit and impact parameters, we apply uniform priors on each of these parameters as well, to allow for the possibility that dynamical interactions have affected the transit timing and impact parameter from the TESS epochs to the present day. When applying a spot model directly through starry, we apply uniform priors on the spot latitude, longitude, contrast ratio, and logarithm of the spot size.
4. Results
Our results are given in Table 2. The maximum likelihood of the stellar activity indicator model is significantly lower than that of the other models. The maximum likelihood  differs by only 0.1 between the starry and polynomial models, but is substantially lower for the third model. The difference in likelihood corresponds to a Bayes factor of ≈10−7 when comparing the stellar activity indicator model to the starry model. In a statistical sense, our starspot model and our simple polynomial model each provide an approximately equally valid fit to the data; both provide a much more plausible fit than the stellar activity indicator model. We note that we also tested models using only one of the two stellar activity indicators, but these performed worse than models using both indicators.
differs by only 0.1 between the starry and polynomial models, but is substantially lower for the third model. The difference in likelihood corresponds to a Bayes factor of ≈10−7 when comparing the stellar activity indicator model to the starry model. In a statistical sense, our starspot model and our simple polynomial model each provide an approximately equally valid fit to the data; both provide a much more plausible fit than the stellar activity indicator model. We note that we also tested models using only one of the two stellar activity indicators, but these performed worse than models using both indicators.
Table 2. Inferred Transit Parameters
| Polynomial Model | Stellar Activity Correlation Model | Starspot Fit | |
|---|---|---|---|
 (km s−1) (km s−1) |
19.6 ± 1.5 | 20.0 ± 1.6 | 19.4 ± 1.5 |

|
0.059 ± 0.002 | 0.060 ± 0.003 | 0.059 ± 0.002 |
| t0 (BJD − 2,457,000) | 1706.6692 ± 0.0010 | 1706.6691 ± 0.0018 | 1706.6693 ± 0.0012 |
| b | 0.18 ± 0.11 | 0.17 ± 0.13 | 0.18 ± 0.12 |
a/
|
20.8 ± 0.7 | 21.2 ± 1.1 | 20.9 ± 0.8 |
| Obliquity (deg) | 14 ± 11 | 5 ± 11 | 12 ± 13 |
| Obliquity (deg), q = 1 | 12 ± 11 | 13 ± 6 | 7 ± 12 |
| Obliquity (deg), α = 1 | 14 ± 13 | 3 ± 11 | 8 ± 15 |
| Spot Amplitude | ⋯ | ⋯ | 0.019 ± 0.005 |
Spot Size ( ) ) |
⋯ | ⋯ | 0.055 ± 0.023 |
| Spot Longitudea (deg) | ⋯ | ⋯ | 26 ± 4 |
| Spot Latitudea (deg) | ⋯ | ⋯ | 28 ± 8 |
| jitter 1 (m s−1) | 1.8 ± 0.9 | 1.5 ± 0.9 | 1.8 ± 0.9 |
| jitter 2 (m s−1) | 8.8 ± 4.4 | 11.9 ± 3.0 | 9.3 ± 5.4 |
| q | 0.54 ± 0.24 | 0.32 ± 0.17 | 0.58 ± 0.24 |
| β | 0.88 ± 0.08 | 0.88 ± 0.11 | 0.85 ± 0.15 |

|
−162.2 | −178.3 | −162.1 |
| Bayes Factor | 0.83 | 9.1 × 10−8 | 1.0 |
Note.
aDefined at BJD − 2,457,000 = 1706.5.Download table as: ASCIITypeset image
This is perhaps not a surprising result: stellar activity indicators are often correlated with RV variations, but not perfectly so (Gomes da Silva et al. 2011; Robertson et al. 2013). As a result, linear models of stellar activity serve as imperfect models to separate planetary and stellar signals, especially on short timescales where the correlation between RVs and stellar activity indicators is even weaker (Meunier et al. 2019). However, because the transit timescale is significantly discrepant from stellar activity timescales and the amplitude of the planetary signal is large, this model still gives results consistent with our other models, despite it being incomplete. This result gives us confidence our results are not likely to be significantly biased by any choices of models that we consider.
All models provide broadly consistent results regarding the projected obliquity. Considering the two families of most plausible models, the median of the projected obliquity posterior varies from 7° to 14° depending on the specific choice of model used. All statistical uncertainties range from 11° to 15°. Using our general polynomial fit, allowing both q and β to vary, we infer a projected obliquity of 14° ± 11°. Likewise, with our starry model, we infer a projected obliquity of 12° ± 13°. As this model provides the highest likelihood fit to the data, we choose this set of values as most representative of our knowledge of the obliquity of the system, but we emphasize that the particular choice of model or likelihood function does not appear to significantly affect the inferred obliquity at the level of more than a few degrees. However, the effect of the choice of model is nonzero, and fixing a specific model will overestimate the inferred precision of the projected obliquity measurement for this system.
We plot posterior draws from our fits for each model in Figure 2, as well as residuals between the data and the best-fitting model. As expected from the likelihood values, visual inspection of the residuals suggests that the polynomial model and starry model perform similarly well—and considerably better than the stellar activity model. In the residuals, correlated structure can be seen during the transit. This is likely due to starspot crossing events during the transit, as regularly seen in the residuals of transit fits to photometric monitoring of planets orbiting active stars (Sanchis-Ojeda et al. 2013; Morris et al. 2017).
Figure 2. Draws from the posterior distributions of a simultaneous fit to the R–M signal and three different noise models. Green curves represent the noise model, while blue curves include the transit signal as well. From top to bottom, the noise models are a simple cubic polynomial fit, a fit regressed against the spectral stellar activity indicators, and a starspot model built with the starry package of Luger et al. (2019). For each model, the residual to the best-fitting model is shown in the small panel below the posterior draws. The polynomial and starspot models provide similar quality fits to the data, both of which find significantly higher log likelihood values than the third fit. Significantly, all give consistent results on the projected spin–orbit obliquity angle of approximately 12° ± 12°. Correlated residuals during the transit observations are likely from starspot crossing events. For visualization purposes, we interpolate the stellar activity indicator regression model between the observations with a cubic spline, although the fitting itself only uses information at the times of the observations, where this model is defined.
Download figure:
Standard image High-resolution imageCegla et al. (2016) provide a relation between the projected obliquity and the true three-dimensional obliquity, if the stellar inclination is known. The stellar inclination can be inferred from a measurement of the stellar rotation period,  , and stellar radius. While there are perhaps significant model uncertainties on the stellar radius, Newton et al. (2019) find the stellar inclination to be consistent with 90° and greater than 70° at 95% confidence. Assuming these values represent a posterior distribution centered on 90° and with a standard deviation of 10°, we then find the true obliquity ψ between the spin of the host star and orbit of the planet to be less than 16 (27) degrees at 1σ (2σ).
, and stellar radius. While there are perhaps significant model uncertainties on the stellar radius, Newton et al. (2019) find the stellar inclination to be consistent with 90° and greater than 70° at 95% confidence. Assuming these values represent a posterior distribution centered on 90° and with a standard deviation of 10°, we then find the true obliquity ψ between the spin of the host star and orbit of the planet to be less than 16 (27) degrees at 1σ (2σ).
5. Discussion
5.1. Transit Timing
The ephemeris from Newton et al. (2019), which includes data from both TESS and Spitzer, predicts a transit time for this transit of BJD − 2,457,000 = 1706.6703 ± 0.0006.13 The ephemeris from Benatti et al. (2019), which includes only TESS data, predicts a transit time of BJD − 2,457,000 = 1706.6903 ± 0.0023. From our data, we measure a transit time of BJD − 2,457,000 = 1706.6693 ± 0.0012. Our result is consistent with the Newton et al. (2019) result at the 1σ level, but is inconsistent with the Benatti et al. (2019) result at 8.1σ. We note that these two predictions, using largely the same original data set, make predictions for the observed epoch that are 8σ discrepant with each other.
While it is possible that the difference in inferred period between these two previous studies is due to the presence of an additional nearby planet perturbing the transiting planet's period between the observed TESS and Spitzer epochs, it is also possible that one or both analyses underestimated their photometric uncertainty. Both analyses used a Gaussian process to model the stellar rotation, but neither directly accounted for the effects of correlated noise due to stellar oscillations. Standing acoustic waves in the stellar photosphere cause oscillations with a period of about five minutes for Sun-like stars (Deubner 1975). These oscillations induce correlated noise in stellar photometric observations that is often non-negligible for stars of a solar mass and radius (Chaplin & Miglio 2013), and may affect the resultant precision in individual transit times inferred from data collected at a two-minute cadence.
Combining the TESS and Spitzer data with our own transit time, we update the orbital period to P = 8.13825 ± 0.00003 days, assuming a linear ephemeris. We note that we do not explicitly model the p-modes either, and if they contribute significantly to the RV variability, with one data point every seven minutes on average, we may be subject to the same underestimation. We encourage other follow-up measurements of the transit, to confirm or refute the presence of transit timing variations in this system.
5.2. Long-term Trend
Over the six hours of the transit, the apparent RV of the star increases at approximately 8 m s−1 hr−1. In Section 3, we model this RV shift using a toy model of a single starspot group moving across the surface of the star, finding this provides an appropriate fit to the data. However, we also use low-order polynomials to attempt to fit the data, finding that a simple heuristic works approximately equally well. This could, in principle, be caused by observing a fraction of a Keplerian orbit from another object orbiting inducing an RV shift on the star. We can easily rule out the wide binary companion as the culprit. From Liu et al. (2002), the RV acceleration from a wide binary companion with mass m at a known separation ρ observed at a distance d is always bounded such that:
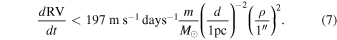
For this companion, the RV trend induced must be no more than 1 m s−1 yr−1, much less than the observed acceleration.
Benatti et al. (2019) show the RV of DS Tuc A is stable at the ≈200 m s−1 level on decadal timescales. Therefore, if the trend observed during the transit were caused by a planet, it must be a planet with a period shorter than ~20 days. If this planet is external to DS Tuc Ab, then it must have m sin i ≥ 10 M . Benatti et al. (2019) rule out any such planets in their analysis of the system. The only plausible planetary companion that could cause this signal but evade detection is a planet in a 1–3 day orbit with a mass of 1–3 times that of Jupiter.
. Benatti et al. (2019) rule out any such planets in their analysis of the system. The only plausible planetary companion that could cause this signal but evade detection is a planet in a 1–3 day orbit with a mass of 1–3 times that of Jupiter.
Such a companion need only be stable for a relatively short time, given the age of the system; a companion similar to this one would likely induce significant TTVs, which could be detected by continued transit monitoring. Our additional observations of the system, taken approximately 30 days after the transit and spread over four nights, do indeed show a signal consistent with a ∼3 M planet in a 2.8 day orbital period. However, this period is also consistent with the measured stellar rotation period from TESS photometry (Figure 3), suggesting that this periodicity and the long-term behavior we observe during the night of the transit are more likely to be explained as starspot-induced modulation.
planet in a 2.8 day orbital period. However, this period is also consistent with the measured stellar rotation period from TESS photometry (Figure 3), suggesting that this periodicity and the long-term behavior we observe during the night of the transit are more likely to be explained as starspot-induced modulation.
Figure 3. (Top) DS Tuc A light curve from the TESS Sector 1 Full-Frame Images, built with the eleanor pipeline of Feinstein et al. (2019). (Bottom) ASAS-SN light curve for the same star, with the TESS light curve overlaid in green. Shaded regions highlight the extent of the TESS light curve overlaid on the ASAS-SN data. While TESS shows a 4% variability on rotational timescales, the star itself varies on multiyear timescales by as much as 30%, suggesting significant starspot coverage on the stellar surface. The brightest observations during the TESS observation window are approximately 10% fainter than the brightest observations with ASAS-SN.
Download figure:
Standard image High-resolution image5.3. Starspot-induced Modulation
The starspot scenario provides a good explanation of the data from the night of the transit. The toy model of Section 3 demands a starspot on the redshifted hemisphere of the star, rotating away from our line of sight during the transit. While we use a single, Gaussian spot in our modeling, in reality spots are non-Gaussian and often appear in groups (e.g., Kilcik et al. 2011).
This may explain the excess variability observed in the second half of our transit. Over this part of the transit, the observed point-to-point variability is larger, which may be the result of the planet crossing a relatively more inhomogeneous hemisphere on observation timescales, causing an increase in the observed variability over this fraction of the observations.
Our median toy model of a single spot, carried over the entire surface of the star, causes a total RV variation of 235 m s−1 in our model; the 68% confidence interval on the peak-to-peak RV shift from this starspot ranges from 191 to 299 m s−1. In fact, we observe a ΔRV of 280 m s−1 over the four nights of data obtained to trace out a single stellar rotation of DS Tuc A. Therefore, a single large spot group can explain both the variability observed during the night of the transit itself and the observed RV scatter on rotational timescales. This does not mean there is only a single spot group on the surface of the star, but rather informs us about the relative asymmetries in spot coverage from hemisphere to hemisphere as the star rotates.
5.4. Characterizing the Starspots of DS Tuc A
The starry model, in addition to matching the observed RV variability, also approximately matches the photometric variability observed during the TESS mission. This particular spot model induces variability at the 1.9% ± 0.4% level at visible wavelengths.
We can compare the modeled spot variability to data from TESS itself. Figure 3 shows a light curve for DS Tuc A from the TESS mission, built using the PSF Flux time series from the eleanor software package of Feinstein et al. (2019). This time series models the PSF of the detector as a 2D Gaussian at each cadence; the parameters describing the Gaussian are allowed to change from cadence to cadence. From these data, a clear rotational signal with a period of 2.85 ± 0.02 days can be seen. It is clear from the TESS data that spot groups on the surface of DS Tuc evolve rapidly: at some points in the month of TESS data, the variability is at the ≈4% level on rotational timescales. A few rotation periods later, the spot amplitude is 1%.
Therefore, the spot model we use is broadly consistent with not only the observed RV signal, but also the photometric signal.
It is important to note that a single spot or spot group, while appropriate for modeling the asymmetries in starspots that define the observed spectroscopic or photometric modulation, does not represent the entire inhomogeneity of the stellar surface. To demonstrate this, Figure 3 also shows photometry for DS Tuc A spanning more than four years from the All-Sky Automated Survey for Supernovae (ASAS-SN) project (Shappee et al. 2014; Kochanek et al. 2017). From this light curve, we can see that the overall observed brightness of the star changes by 30% over four years. At the time of the TESS data, the star is approximately 10% fainter than at its 2014 levels, placing a lower limit on the overall spottedness of the star. Although the asymmetries in the spot distribution cause photometric modulations at the few percent level, the ASAS-SN data imply that both hemispheres are more spotted than the relative difference in spottedness between the two hemispheres.
5.5. The Power of Obliquity Measurements of Young Stars
We have seen from these data that the RV of DS Tuc A varies by nearly 300 m s−1 on rotational timescales. However, because the surface is relatively consistent on transit timescales, the R–M signal is relatively easy to disentangle from the rotational modulation despite being an order of magnitude smaller in amplitude.
Recent work has shown orbits of planets can still be detected in the face of extreme stellar activity (Barragán et al. 2019), and the Doppler method still remains the most effective way to measure masses of planets spectroscopically. However, even without a mass, we are able to confirm this planet, which had only been statistically validated in previous works. From the R–M detection, we can be sure this event is the result of an object transiting the surface of DS Tuc A. As the transit depth from TESS precludes the possibility this event is caused by a transiting brown dwarf or low-mass star, the only possible cause for this observed event is a bona fide transiting planet. DS Tuc Ab thus joins a small number of planets that have been confirmed through the secure detection of their R–M signal, including Kepler-8b (Jenkins et al. 2010) and the Kepler-89/KOI-94 system (Hirano et al. 2012). DS Tuc Ab is the first member of this class discovered by the TESS mission, although future planet candidates discovered around young, active, and rapidly rotating stars discovered as this mission completes its photometric survey of the sky may provide additional opportunities to repeat this procedure.
DS Tuc A has a measured  of 18.3 ± 1.8 km s−1, making precision RV work challenging. More massive stars that lack convective outer layers can rotate at similar speeds (e.g., McQuillan et al. 2014). The R–M signal is proportional to the size of the planet and the rotational velocity of the star, and is independent of the mass of either object. For rapidly rotating stars or large, low-density planets, it is possible to have an R–M signal with amplitude larger than that of the Doppler signal. Future TESS discoveries of young planets or those orbiting massive, rapidly rotating stars may thus find that the best path to confirmation is through observation and characterization of the R–M signal.
of 18.3 ± 1.8 km s−1, making precision RV work challenging. More massive stars that lack convective outer layers can rotate at similar speeds (e.g., McQuillan et al. 2014). The R–M signal is proportional to the size of the planet and the rotational velocity of the star, and is independent of the mass of either object. For rapidly rotating stars or large, low-density planets, it is possible to have an R–M signal with amplitude larger than that of the Doppler signal. Future TESS discoveries of young planets or those orbiting massive, rapidly rotating stars may thus find that the best path to confirmation is through observation and characterization of the R–M signal.
For young, rapidly rotating stars, stellar activity can place limitations upon the achievable RV precision. Large spots can affect the shapes of spectral features, changing the spectrum of the star from observation to observation. A template observation of the star may not be representative of the data at another well-separated epoch, limiting the achievable precision. In this work, we obtained a stellar template on the night of the observations, enabling us to achieve a precision of 3–5 m s−1 at most epochs. Later observations, although targeted to achieve an S/N similar to that of our original observations, typically achieve a precision of 7–9 m s−1. This may be result of line shape variations combined with pipeline systematic effects induced by the interplay between individual iodine and stellar features in the spectra due to a changing barycentric correction between the template and science exposures. To mitigate these effects for future similar observations of young stars, we encourage future observers to obtain their template spectra, if any are required, as near the transit as feasible, so that the template reflects a state of the stellar surface similar to the RV observations.
5.5.1. Differential Rotation
Differential rotation, in which the equatorial latitudes of a star rotate more quickly than its polar latitudes, can be significant for young stars (Waite et al. 2017), and therefore may complicate future analyses of the obliquity of young planetary systems. To quantify the significance of differential rotation, we perform simulations of a rotating star, comparing the observed R–M signal for a star rotating as a solid body to a star with differential rotation such that its equatorial latitudes are rotating with an angular velocity twice that of its polar latitudes. This level of differential rotation is several times greater than the largest values observed for young stars (e.g., Fröhlich et al. 2012)
At its equator, the simulated star has a rotational velocity of 18.3 km s−1 and is viewed perfectly edge-on. We use a simple linear limb darkening model for this experiment, with u = 0.64. We do not place any spots on the surface of this star. We then inject a planet the size of Jupiter onto an orbit that transits the surface of this star, measuring the R–M effect from this orbit.
Not surprisingly, for low projected obliquities, the effect of differential rotation on the observed signal is small. If the planet crosses the surface of the star occulting a chord of constant latitude, then these data will not sample any of the stellar differential rotation. At higher obliquities, as the planet transits regions of the star with different angular velocities at different times, the R–M signal begins to deviate from the uniform rotation case.
Figure 4 shows the difference between the R–M signal for this star with strong differential rotation and the best-fit signal for a uniformly rotating star at different impact parameters, for a transiting planet with λ = 90°. At b = 0, the planet occults only the central longitudes of the star, where the radial component of the rotational velocity is zero. As a result, the R–M signal for this configuration is zero regardless of differential rotation. Similarly, at b = 1, the planet only transits a small range of latitudes, so it does not sample sufficient regions of the star for models of differential or solid body rotation to be distinguished. However, at intermediate impact parameters, the difference between these models can approach 2 m s−1, which could be detectable in some cases. In the future, detections of misaligned planets around rapidly rotating stars may provide opportunities to clearly detect differential rotation.
Figure 4. Difference in best-fitting R–M models for a differentially rotating star and one rotating as a solid body at various impact parameters. At b = 0, there is no dependence on differential rotation, nor is there for mutually inclined systems. These curves all correspond to λ = 90°, for a star rotating with an angular velocity twice that at its equator as near its poles, and with an equatorial velocity of 18 km s−1. Even in this idealized case, the maximum discrepancy between the two models is 2 m s−1, so most observations will not be able to detect differential rotation in a single transit.
Download figure:
Standard image High-resolution imageIn the case of DS Tuc Ab, its low obliquity means this system is not a viable candidate to detect differential rotation. We verify this claim by rerunning our spot model fit, allowing the differential rotation shear value α to take any value in the range [0, 1] with a uniform prior in that range. The resultant posterior is unconstrained: there is power at all values of α and our 95% confidence interval spans the range [0, 0.88]. Significantly, we note that including α does not affect our measured projected obliquity: in this run, we measure the projected obliquity λ = 12° ± 14°, consistent with the 12 ± 13 value we find with no differential rotation.
However, flat systems with multiple planets may provide an opportunity to detect differential rotation. In this work, we infer a rotational velocity of 19.4 ± 1.5 km s−1 for DS Tuc A. This is larger than what is measured by Benatti et al. (2019) and Newton et al. (2019), albeit only at the 1σ level. Observations of two planets orbiting the same star at different impact parameters may provide different inferred rotational velocities, even if both have the same low projected obliquity, if the star has strong differential rotation. The recently announced four-planet system V1298 Tau (David et al. 2019), a young solar analog with an age of 23 ± 4 Myr, may provide such an opportunity in the near future.
5.5.2. R–M Observations and EPRV Pipelines
The Doppler shift observed through the R–M effect is, of course, not an intrinsic Doppler shift, but rather a change in the shape of the spectral lines. The efficacy of this method is reliant on the ability to measure the velocity shift in line centroid through RV processing strategies, which often fit a single, unchanging template to all observations, varying only the velocity shift of this template.
Previous analyses have tested the ability of different pipelines to produce the expected velocity shifts. For example, Winn et al. (2008) and Johnson et al. (2008) simulated Keck/HIRES data for HAT-P-1 and TRES-2, and analyzed them with the California Planet Search reduction pipeline, which is very similar to the pipeline used in our DS Tuc analysis. Both these authors found that their pipeline recovered the expected transit shifts. Winn et al. (2005) and Hirano et al. (2010) note that the potential discrepancies may be larger for stars with large  . They developed analytic formulae for the analysis of R–M signals, finding accurate representations of the measurements of cross-correlation analyses for Keck/HIRES and Subaru data, respectively.
. They developed analytic formulae for the analysis of R–M signals, finding accurate representations of the measurements of cross-correlation analyses for Keck/HIRES and Subaru data, respectively.
More recent work has provided a detailed comparison between R–M and Doppler tomographic methods. Brown et al. (2017) compare HARPS spectra of a series of hot Jupiters, and measure their stellar obliquities inferred through the R–M and Doppler tomographic methods. They find the results to be consistent with each other whether or not the corrections of Hirano et al. (2010) are applied, including for stars with  values larger than DS Tuc A. There are several other studies of planets orbiting much more rapidly rotating stars that use similar methods (e.g., Triaud et al. 2009; Gandolfi et al. 2010).
values larger than DS Tuc A. There are several other studies of planets orbiting much more rapidly rotating stars that use similar methods (e.g., Triaud et al. 2009; Gandolfi et al. 2010).
We verify that our results are not significantly affected by biases induced by the RV pipeline. First, we apply the correction due to this effect produced by Winn et al. (2005) for HD 209458 and scaled to the rotational velocity of DS Tuc A, using our same spot modeling procedure with a single spot as described in Section 3.1. In this case, we measure a projected obliquity of 8° ± 12°, consistent with that observed previously. The  of this model is −162.8, suggesting in this case that the correction of Winn et al. (2005) provides a very slightly worse fit than the fit without the correction. As expected, this correction reduces the inferred rotational velocity, from 19.4 ± 1.5 to 17.7 ± 1.7 km s−1, similar to the effect observed by Brown et al. (2017).
of this model is −162.8, suggesting in this case that the correction of Winn et al. (2005) provides a very slightly worse fit than the fit without the correction. As expected, this correction reduces the inferred rotational velocity, from 19.4 ± 1.5 to 17.7 ± 1.7 km s−1, similar to the effect observed by Brown et al. (2017).
Additionally, we approximate the PFS pipeline by modeling the line shape variations of a single line transited by a planet. We model the velocity field of a simulated star with a  of 18 km s−1, following Short et al. (2018), who use this model to derive accurate formulae for the R–M signal. We apply limb darkening parameters consistent with that observed for DS Tuc A. We use this model to build a line profile, then add a Gaussian "bump" to represent the transiting planet, following the method of Collier Cameron et al. (2010). At each step, we infer the velocity change in the centroid of the spectral line and also cross-correlate with a template model of the spectral line with no transiting planet. We infer the measured RV by fitting a parabola to the cross-correlation result, finding that while there are differences, they are small relative to the size of the signal. The largest discrepancies are at ingress and egress—but importantly, they are symmetric across the transit, so these discrepancies will not significantly affect the measured obliquity.
of 18 km s−1, following Short et al. (2018), who use this model to derive accurate formulae for the R–M signal. We apply limb darkening parameters consistent with that observed for DS Tuc A. We use this model to build a line profile, then add a Gaussian "bump" to represent the transiting planet, following the method of Collier Cameron et al. (2010). At each step, we infer the velocity change in the centroid of the spectral line and also cross-correlate with a template model of the spectral line with no transiting planet. We infer the measured RV by fitting a parabola to the cross-correlation result, finding that while there are differences, they are small relative to the size of the signal. The largest discrepancies are at ingress and egress—but importantly, they are symmetric across the transit, so these discrepancies will not significantly affect the measured obliquity.
This result is not surprising. Standard RV processing pipelines have been shown to produce measured obliquities similar to those of newer, data-driven approaches, with respect to measuring R–M signals (Bedell et al. 2019). Discrepancies are generally largest at transit ingress and egress, when the line profile variations are limited to the wings, and our flexible stellar activity model could plausibly account for any short-term systematic offsets. Moreover, given that the measurement of obliquity comes from the potential asymmetry between the blueshifted and redshifted components of the RV curve, any effects from the RV processing pipeline that are symmetric around the RV of the star may affect the measured  but should not systematically bias the inferred obliquity.
but should not systematically bias the inferred obliquity.
In general, Doppler tomography analyses and R–M analyses aim to measure the same effect. Doppler tomography, providing a detailed analysis of line profile variations, is feasible with an unstabilized spectrograph, while R–M requires a PRV instrument with few m s−1 precision. On the other hand, R–M observations provide a more straightforward opportunity to better understand the underlying starspot distribution through the measurement of intranight RV variations. A significant advantage of the R–M method is the development of open-source software built to enable these analyses, while there is no publicly available analysis pipeline for Doppler tomographic analyses. Both methods are able to provide useful results with instruments like PFS, and each provides additional information in some cases that the other cannot provide alone.
6. Conclusions
Batygin (2012) suggest that wide binary companions may effectively tilt protoplanetary disks, such that a fraction of young, short-period planets that migrated through a smooth disk process may nonetheless have high inclinations. We look for evidence of this hypothesis by measuring the R–M effect for DS Tuc Ab, a ≈ 40 Myr planet transiting a Sun-like star in the Tuc–Hor association.
The orbit of DS Tuc Ab has a low projected obliquity of λ = 12° ± 13° relative to the spin of its host star. A single system with a low obliquity neither confirms nor rules out the hypothesis of Batygin (2012), but does provide a first data point. This is the youngest planet for which the R–M effect has been measured. As TESS observes more stars that are members of young moving groups, and as data processing techniques with that instrument become more sophisticated, additional planets will be discovered to continue to test this hypothesis. This result aligns with the conclusions of Zanazzi & Lai (2018), who argue that the formation of a warm, giant planet can can reduce or even entirely suppress the excitation of a spin–orbit misalignment, depending on the timescale for accretion onto the planet relative to the disk-binary precession period. Similar characterization of additional systems like this one may thus be useful in understanding the timescale for giant planet formation in protoplanetary disks.
Zhou et al. (2019) use PFS data of this system for a Doppler tomographic analysis, also finding a low projected obliquity. Oshagh et al. (2018) note that changes in the distribution of starspots on highly active stars can affect the measured obliquity by as much as 40°, making additional, complementary observations of this system an important test of the obliquity. In this case, observations of multiple transits spread over months enable a confident interpretation of the measurements reported in both Zhou et al. (2019) and in this work.
DS Tuc Ab is one of a small number of planets to be confirmed by a detection of its R–M signal rather than its spectroscopic orbit. This approach may be the optimal strategy for future confirmation of young planets orbiting rapidly rotating stars. While the RV of the star varies on rotational period timescales at the 300 m s−1 level, it does so relatively smoothly over transit timescales, enabling us to cleanly disentangle the stellar and planetary signals. While this planet would require a dedicated series of many spectra and a detailed data-driven analysis to measure a spectroscopic orbit, the R–M signal is visible by eye in observations from a single night. For certain systems, in addition to a more amenable noise profile, the amplitude of the R–M signal can be larger than the Doppler amplitude. Observations similar to these should be achievable for more young planets as they are discovered, which will elucidate the end states of planet formation in protoplanetary disks.
We thank George Zhou (Center for Astrophysics ∣ Harvard and Smithsonian), Leslie Rogers (University of Chicago), and Chris Spalding (Yale) for conversations that improved the quality of this manuscript.
This paper includes data gathered with the 6.5 m Magellan Telescopes located at Las Campanas Observatory, Chile.
This research was enabled by the Exostar19 program at the Kavli Institute for Theoretical Physics at UC Santa Barbara, which was supported in part by the National Science Foundation under grant No. NSF PHY-1748958.
Work by B.T.M. was performed in part under contract with the Jet Propulsion Laboratory (JPL) funded by NASA through the Sagan Fellowship Program executed by the NASA Exoplanet Science Institute.
J.K.T. acknowledges support for this work provided by NASA through Hubble Fellowship grant HST-HF2-51399.001 awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., for NASA, under contract NAS5-26555.
This material is based upon work supported by the National Science Foundation Graduate Research Fellowship Program under grant No. DGE-1746045. Any opinions, findings, conclusions, or recommendations expressed in this material are those of the author(s), and do not necessarily reflect the views of the National Science Foundation.
This paper includes data collected by the TESS mission. Funding for the TESS mission is provided by the NASA Explorer Program.
TESS data were obtained from the Mikulski Archive for Space Telescopes (MAST). STScI is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555. Support for MAST is provided by the NASA Office of Space Science via grant NNX13AC07G and by other grants and contracts.
Facilities: Magellan: Clay (Planet Finder Spectrograph) - , TESS - , ASAS-SN. -
Software: numpy (Van Der Walt et al. 2011), matplotlib (Hunter 2007), scipy (Jones et al. 2001) astropy (Astropy Collaboration et al. 2018), eleanor (Feinstein et al. 2019), starry (Luger et al. 2019), emcee (Foreman-Mackey et al. 2013).
Footnotes
- *
This paper includes data gathered with the 6.5 m Magellan Telescopes located at Las Campanas Observatory, Chile.
- 10
Here and throughout, we refer to obliquity exclusively to describe the relative angle between the spin of the star and the orbit of the planet, not the relation between the spin of the planet and its orbit, which may be detectable for some systems in the near future (Millholland & Laughlin 2019).
- 11
- 12
For a derivation, see https://rodluger.github.io/starry/v1.0.0/notebooks/RossiterMcLaughlin.html, which is also included as a notebook in the arXiv source material of this manuscript.
- 13
Here, we specifically mean Barycentric Dynamical Time (TDB), which is the time standard used by the Kepler and TESS missions, and unlike Julian Date, is unaffected by leap seconds.







