- 1Department of Computer Science, Heinz Nixdorf Institute, University of Paderborn, Paderborn, Germany
- 2iMinds, Ghent University, Ghent, Belgium
- 3Computer Science and Communications Research Unit, Faculty of Science, Technology and Communication, University of Luxembourg, Luxembourg City, Luxembourg
- 4Laboratory of Socioecology and Social Evolution, Department of Biology, KU Leuven, Leuven, Belgium
- 5Institute for Software & Systems Engineering, University of Augsburg, Augsburg, Germany
- 6Department of Computer Applications in Science & Engineering, Barcelona Supercomputing Center (BSC), Barcelona, Spain
- 7Faculty of Computer Science, Otto von Guericke University Magdeburg, Magdeburg, Germany
- 8Department of Electronics, University of York, York, UK
- 9Robotics, Evolution and Art Laboratory, IT-University of Copenhagen, Copenhagen, Denmark
- 10Computer Architecture and Languages Laboratory, Faculty of Electrical Engineering and Computer Science, Institute of Computer Science, University of Maribor, Maribor, Slovenia
Hybrid societies are self-organizing, collective systems, which are composed of different components, for example, natural and artificial parts (bio-hybrid) or human beings interacting with and through technical systems (socio-technical). Many different disciplines investigate methods and systems closely related to the design of hybrid societies. A stronger collaboration between these disciplines could allow for re-use of methods and create significant synergies. We identify three main areas of challenges in the design of self-organizing hybrid societies. First, we identify the formalization challenge. There is an urgent need for a generic model that allows a description and comparison of collective hybrid societies. Second, we identify the system design challenge. Starting from the formal specification of the system, we need to develop an integrated design process. Third, we identify the challenge of interdisciplinarity. Current research on self-organizing hybrid societies stretches over many different fields and hence requires the re-use and synthesis of methods at intersections between disciplines. We then conclude by presenting our perspective for future approaches with high potential in this area.
1. Introduction
This paper originates from a small international workshop on “Methods for Self-Organizing Distributed Systems” that was held in Laubusch, Germany, during October 2015. We name several challenges and give our perspectives for the field of hybrid societies [cf. Eiben (2014) and Prokopenko (2014)]. In general, hybrid societies are made of different components instead of having a homogeneous identity. We call them “societies” because the components possess individual agency and interact persistently. Such societies can be comprised both natural and artificial agents (Baxter and Sommerville, 2010; Halloy et al., 2013; Schmickl et al., 2013; Hamann et al., 2015) or different types of artificial agents only (Dorigo et al., 2013). We focus on self-organizing collective hybrid societies that are characterized by multiple interactions of agents, positive and negative feedback processes, and fluctuations (Ashby, 1947; Bonabeau et al., 1999; Camazine et al., 2001; Omicini and Viroli, 2011; Heylighen, 2016). Often, these systems show collective behavior indicated by the emergence of global spatial and/or temporal patterns (Serugendo et al., 2006; Attanasi et al., 2014; Popkin, 2016). Furthermore, hybrid societies are describable on a microscopic level, the level of an individual agent, and a macroscopic level, the level of the whole society (Schelling, 1978; Alexander et al., 1987; Schillo et al., 2000; Hamann et al., 2014). We want to design and determine the artificial part of these systems, although the artificial subpopulation is in contact with a natural subpopulation in hybrid societies.
Typical examples of hybrid societies are investigated in the project ASSISI|bf (Schmickl et al., 2013) where robots closely interact either with groups of bees or fish. Such systems require different approaches than those developed for multi-agent systems because they are heterogeneous and while the robots are variably programmable the biological agents (bees and fish) have a determined behavior. The ASSISI|bf system heavily relies on social aspects because the robots need to learn the “social language” (Schmickl et al., 2013) of bees/fish to trigger desired behaviors. It is a hybrid system because the robot–animal interaction is not only in one way but also the animals determine the system’s further development. Similarly, we have hybrid societies in socio-technical systems where human beings closely interact with technological artifacts (Baxter and Sommerville, 2010; Smirnov et al., 2014; D’Orsogna and Perc, 2015; Helbing et al., 2015).
We identify three common, primary challenges in the design of hybrid societies (see Figure 1). Each is discussed in detail, supplemented by additional secondary challenges, and we give our perspective on future approaches with high potential.

Figure 1. Overview of design challenges in hybrid societies: primary challenge A – formalization, primary challenge B – system design, and primary challenge C – interdisciplinarity.
2. Primary Challenge A: Formalization of Hybrid Societies
The analysis of hybrid societies using tools of mathematics and computer science is essential to gain deep insights into the dynamics and prominent principles of hybrid systems. Besides allowing for predictions, the formal approach also guides one’s thoughts when designing hybrid societies. The formalization of hybrid societies is the precondition to move from formal specifications to an integrated design process.
2.1. Purpose of Formalization
From our experience in work with collective hybrid societies, we have the strong belief that our field of research requires a tremendous effort to develop a generic model. Hence, a grand challenge of the design of collective behavior in hybrid societies is to develop an appropriate generic formalization. A truly generic formal model would overcome the diversity of methods and models in the field. If not completely generic, we would at least require a methodology that allows to model a large range of different collective hybrid societies. The purpose of a generic model is to understand the desired system and to gain deep insights. Formalization is necessary to achieve a good understanding of a system’s inner dynamics and, if possible, to predict its outcome. With the optimal model, we could predict future behaviors and effects of hybrid societies. Such a model would permit to analyze a wide variety of collective systems, enable rigorous mathematical comparisons, and help to understand potential problems in system design before realization in simulation, and hardware was achieved.
2.2. Requirements and Actions for a Formalization
The formalization approach should be generic and applicable in many domains sharing essential system features. The development of such modeling techniques requires, however, to unify methods, concepts, and definitions from many different fields. It requires a high degree of integration, knowledge about each of these domains, and a high convertibility of the model. First steps toward a unified methodology have been made, for example, in the fields of socio-technical systems (Baxter and Sommerville, 2010; Jones et al., 2013; Schöttl and Lindemann, 2015) and swarm robotics (Lerman et al., 2005; Brambilla et al., 2013). Models originating from natural sciences are limited in representing typical abilities of agents and also modeling the emergence of self-organizing artifacts is challenging (see Sec. 2.6). A generic framework reflecting domain-specific characteristics while accurately capturing the evolution and dynamics of collective behavior, both on the micro- and macroscopic level, needs to be established.
2.3. Secondary Challenge: Diversity of Methods
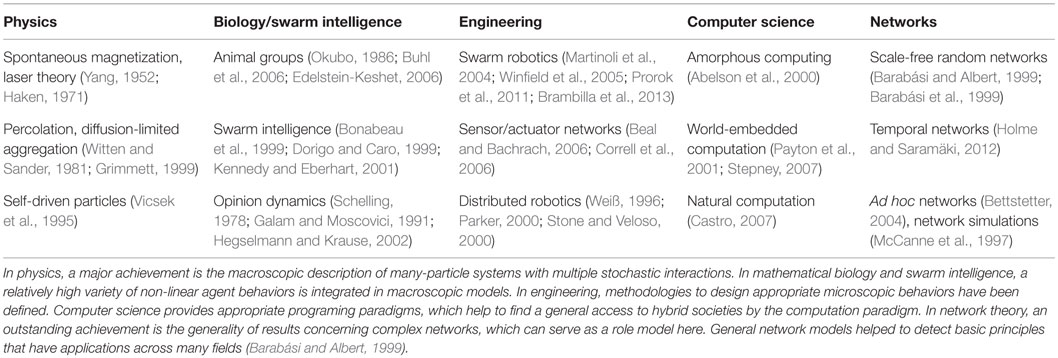
Depending on the system modeled, as well as the type of questions asked, multiple approaches have been developed ranging from purely mathematical equations to spatial multi-agent systems. The total amount of modeling and investigation techniques for homogeneous and heterogeneous collective systems is huge and spans fields such as collective animal behavior, statistical physics, network theory, control theory, opinion dynamics, and diverse subfields of computer science. In order to give a little, incomplete overview, we cite only a few of these, see Table 1. Despite the strict column-wise presentation of methods, there exist already approaches that combine several methods from different fields, such as the combination of game theory with networks (Perc and Szolnoki, 2010), percolation and networks (Piraveenan et al., 2013a), and hybrid systems with temporal networks (Boerkoel and Durfee, 2013). Furthermore, the field of evolutionary game theory investigates hybrid societies, especially the interaction of agents also with reference to collective behavior and self-organization (Perc and Szolnoki, 2010; Perc and Grigolini, 2013). However, the developed models often abstract away proximate mechanisms, that is, the behavioral rules that generate the spatio-temporal dynamics of collective systems (André, 2014). Partially due to the extreme diversity of methods, it is difficult to compare hybrid societies or their models. A generic, formal modeling approach of collective hybrid societies would help to overcome that problem.
2.4. Secondary Challenge: System Complexity
Another challenge is the complexity of hybrid societies due to self-organization that contains by definition a multitude of locally interacting agents. Local interactions between agents create dynamic environments, which are complex to model. The agents operate locally but can trigger emergent global patterns; we have different types of agents, and they often live in dynamic environments, which are challenging to model.
For example, a difficulty specific to self-organization is to link the model that describes the global behavior of the system to the model that describes the behavior of the individuals. Defining the so-called micro–macro link is a fundamental issue in both directions (Schelling, 1978; Hamann and Wörn, 2008). Macro-to-micro means that a certain global behavior is required; however, the respective individual behaviors are unknown. Micro-to-macro is the challenge of predicting the macro-behavior for a given micro-behavior. Particular internal states of these agents may be essential, e.g., the internal energy levels are crucial especially in flying agents (e.g., quadrocopters) or forest ecosystems (Zamuda and Brest, 2013). The formal approach has to address these internal states and model their dynamics. Local and global correlations between these internal states add another challenge.
In summary, we have the dynamics of the internal states and local interactions of individual agents on the one side and the overall dynamics of the global system on the other side. The challenge is to find the link between these two sides, which is key to understand and formalize hybrid societies.
2.5. Shortcomings in the State of the Art
The vast number of methods of hybrid societies comes with individual shortcomings. We discuss only a few that may serve as representative examples. The methods of formal specification from the field of software engineering [e.g., see Hoare (1978) and Jackson (2006)] are challenged by the number of interacting entities and their local interactions because the size of state space grows with the size of a collective (Brambilla et al., 2014). When this is coupled with the complexity of the dynamic environments that we typically expect these agents to exist in, we rapidly find ourselves in need of novel techniques to model and explain the dynamics of our systems. Concise mathematical descriptions of systems, such as methods from chemistry (van Kampen, 1992), are typically incapable to model complex agent-to-agent interactions, especially in the case where spatiality plays a central role (Ohkubo et al., 2008). Computational models often require rather strong abstractions for the sake of run-time efficiency. Agent-based models typically require an increased number of parameters with increasing system complexity which challenges their significance (Mayer et al., 2010).
2.6. Our Perspective and Approaches
Engineered hybrid societies are complex, and therefore it is difficult to develop de novo novel mathematical formalisms. A common option is to use frameworks that were developed for natural systems to formalize artificial systems when they share key features. In general, two aspects are formalized: (1) the behavioral mechanisms themselves (at microscopic or macroscopic level) and (2) the process that leads to these mechanisms (e.g., evolution in natural systems, machine learning in artificial systems).
Chemistry and statistical physics provide formal, mechanistic descriptions of hybrid systems. They are the disciplines that inspired, for example within swarm robotics, the most commonly used modeling frameworks (Brambilla et al., 2013), such as the master equation approach from chemistry (Martinoli et al., 1999) and use of Fokker–Planck and Langevin equations from statistical physics (Hamann and Wörn, 2008). However, the main challenge consists in going beyond the typical assumptions of these approaches that are intrinsic for large numbers of components [“Avogadro-large,” cf. Beni (2005)] and lack capabilities to model cognition and communication. Hence, collaborations with physicists and theoretical chemists could help to extend these models, to account for smaller system sizes, and to model cognition, and to explicit communication.
Less attention has been paid to the formalization of processes leading to self-organization as done in theoretical evolutionary biology and machine learning. In the first case, evolutionary game theory (Nowak, 2006) with infinite (e.g., differential equations) and finite (e.g., birth–death processes) populations provides promising approaches but is limited to the evolution of finite discrete strategies, rather than continuous behavioral traits. Reinforcement learning is a framework suited for single-agent systems (Kaelbling et al., 1996) and in some cases collective systems (Wolpert and Tumer, 1999). In multi-agent settings, machine learning struggles with the combinatorial explosion of possibilities, which is usually approached with sophisticated methods that reduce the search space (Matarić, 1997). To the best of our knowledge, machine learning techniques have never been extended to hybrid societies.
3. Primary Challenge B: System Design of Hybrid Societies
Even if we assume that we have a formal specification of our hybrid society already, then the actual system design is still a big challenge. We would like to define an integrated process that implements the step from a specification of a self-organizing collective system to the actual real-world system and its deployment in the field. In addition, we have to consider typical requirements for engineered systems, such as safety, reliability, and stability. Also note that we consciously take an engineering perspective on hybrid societies, hence assuming that such self-organizing collective systems can actually be designed. This hypothesis is in line with assumptions made in standard approaches, such as swarm robotics (Martinoli, 1999; Brambilla et al., 2013). However, one can also take the perspective that self-organizing systems can at most be guided but not fully determined (Prokopenko, 2009).
3.1. Requirements and Actions for System Design
Moving from a specification of a hybrid society to a verified implementation on actual hardware remains difficult. Dealing with issues such as time, non-determinism, and scale presents significant challenges to formal methods. Hybrid societies can be designed with a smaller effort for pre-specified environments but for real-world implementations quality characteristics have to be determined (Mahendra Rajah et al., 2005; Levi and Kernbach, 2010; Brambilla et al., 2013). Formal methods help to develop tools that ensure system properties, a level of safety, and guaranteed safe software from specification to implementation.
The design for reliability and stability needs to be addressed before we are able to deploy many hybrid societies in the real world. The stochasticity and the autonomy present in such systems make assuring reliability a difficult task. Therefore, developing such systems needs to provide evaluation tools that allows for measuring those aspects in a representative way.
3.2. Secondary Challenge: Stochasticity, Uncertainty, Unpredictability
Most real-world environments show a high degree of stochasticity, which makes it challenging to deploy hybrid societies in real-world applications. We need methodologies to deal with known uncertainties but also to deal with unforeseen uncertainties. For collective behaviors, we are missing a general model that could be used to verify the system against the expected behaviors. In addition, there might be even unpredictable behaviors [cf., emergent behavior Matarić (1993) and Bedau (2002)] that prevent us from assuring that the system never leaves the set of safe states.
3.3. Secondary Challenge: Dynamic Environments, Run-Time Decisions, and Open Systems
Related to the above complex problems, we also face the challenge of dynamic environments that require non-trivial run-time decisions of our system. Run-time decisions and coupling the collective hybrid society with other systems at run-time require new methodologies. Especially systems with high requirements for robustness operating in dynamic environments have to be able to appropriately self-adapt their behaviors and organization structure (e.g., topology). The required time for non-productive reorganization and adaptation processes should be minimal.
If we allow dynamic changes of the system size, that is, we have an open system, then we need to tackle the challenge of scalability at runtime as well. This adds additional uncertainties introduced by added or removed system components. These changes need to be balanced by the system at run-time to establish a stable and robust system behavior. We often face difficulties when attempting to make guarantees about the behaviors of our systems and in the scenarios when existing techniques can be used they often model a fixed number of agents, making our proofs meaningless as the size of our collective changes dynamically.
3.4. Secondary Challenge: Design of Feedbacks for Self-Organization and User Feedback
Natural collective systems exhibit different features that are remarkable, such as flexibility, adaptability, and robustness. To achieve these through self-organization, they resort to positive and negative feedback mechanisms, the ability to amplify and weaken local individual decisions. The careful design of appropriate feedback processes requires special attention and sophisticated design methods. Besides behavioral feedbacks, collective systems also rely on certain network topologies and network properties, such as power-law degree distributions (scale-free networks), that increase the system’s robustness to the loss of connections (Albert et al., 2000; Crucitti et al., 2003; Piraveenan et al., 2013b).
Another feature is that of scale-free correlations (Cavagna et al., 2010), which is the ability of collective systems to influence far-away neighbors independently of the system size, by still resorting to local interactions only. Besides research on modulating positive feedback (Valentini et al., 2014), the negative feedback and scale-free correlations have received little attention yet and are challenging.
A notable quality of deployed systems is user behavior feeding back steadily into the system. This inevitably entails risks such as collusion, free-riding, or other exploitative and destabilizing actions. The additional challenges, for example in terms of robustness and reliability, therefore need to be considered and firmly rooted in the system design.
3.5. Our Perspective and Approaches
Once deployed in the field, bugs are likely to appear in ways unforeseen by the formalization process. This limitation of the formalization task is termed reality gap in robotics and has been studied in recent years. Solutions range from the restriction of the search space (Koos et al., 2013; Cully et al., 2015) to the design of behaviors during the deployment of the system (Watson et al., 2002; Bredeche and Montanier, 2010). The design of a hybrid-society system could benefit from these approaches.
In order to allow our system to adapt to changes in its dynamic environment, it requires a sufficient degree of freedom enabling it to self-optimize and to show reliable behavior. We need to allow for methods of self-repair (Ismail and Timmis, 2010) and self-sustainability (Bredeche and Montanier, 2010), which adds even more complexity to the system and increases the challenge of system design. Incorporating the capability for autonomous reasoning (Anshakov and Gergely, 2010) certainly improves the system but at first it increases its complexity.
4. Primary Challenge C: Interdisciplinarity in Hybrid Society Research
As the reliance on knowledge gained from other scientific disciplines grows, so too does the need for researchers from all fields to be prepared to learn from the insights and techniques of others. The investigated problems are becoming too complex to stay within the scope of a single discipline, and hence, interdisciplinary research is becoming more popular (Helbing et al., 2015). Hybrid societies are an inherently interdisciplinary problem domain, thus the inclusion of findings from various disciplines is essential for their structural and algorithmic design [e.g., combination of results from plant science, robotics, and architecture (Hamann et al., 2015)]. Interdisciplinarity is crucial to produce a valid model of a system observed in another discipline, or to take inspiration from another discipline in the design of systems. From an engineering perspective, being inspired by biology, chemistry, and sociology is becoming common place. However, engaging in a meaningful way with another discipline can be challenging and often, not fruitful in part because an approach remains rather superficial where an extra effort with additional overhead would have been required.
4.1. Requirements and Actions for Interdisciplinarity
Engineering has much to offer to the life sciences, but benefits of engagement must be bi-lateral, so that all disciplines benefit from the collaboration. In particular, the contribution of computer science should go beyond that of a mere service to life sciences but instead establish a bidirectional interaction that also scientifically enriches computer science. For example in the context of bio-hybrid societies, modeling and simulation can be an effective vehicle for collaborations between computer scientists (e.g., multi-agent simulations) and biologists (e.g., behavioral models), with computational models being useful to help understand challenges in behavioral biology, yet providing a formal background and inspiration to the creation of an artificial system, for example based on behavioral models of animals (Schmickl and Hamann, 2011) or growth models of plants (Zamuda and Brest, 2013; Hamann et al., 2015). We should try to get inspiration from biology and sociology while lending our skill sets to the understanding of other fields. However, interdisciplinary research in hybrid societies has proven to be challenging.
4.2. Secondary Challenge: Common Language
Despite our best will to ensure interdisciplinarity, it remains difficult to achieve in practice. These difficulties stem from the disparity in vocabulary, the different methodologies used, and a general lack of understanding of the way of thinking and the tools available on each side. Time is needed to develop an interdisciplinary collaboration. A common language needs to be developed so that deep and meaningful collaborations are possible.
4.3. Secondary Challenge: Integration of Methods
Once a simple mutual understanding of the available methods and present problems is obtained, it is tempting to merely transfer a method from one field to the other and to directly apply it to a particular problem. However, mastering the complex problems at hand and lastingly improving these systems goes beyond applying existing results but requires true interdisciplinary collaboration. Providing a broad set of insightful tools, only highly integrated research on novel systems leads to a meaningful design method for hybrid societies. Prime examples of successful integration of methods are the integration of robots and fish (Marras and Porfiri, 2012) and the automatic analysis of social networks in honeybees (Wario et al., 2015). Again, establishing such a deep understanding of the other field requires time.
4.4. Secondary Challenge: Interdisciplinarity in a Mono-Disciplinary World
Despite the success of interdisciplinary research and a lot of hype and lip service in favor of interdisciplinarity, realities still look different. Many institutions and traditions in research are still forming tiny mono-disciplinary worlds. Hence, there is a challenge for individual researchers to fulfill their own discipline’s requirements in terms of measures of success.
4.5. Our Perspective and Approaches
A probably obvious solution is to enable the human factor and to form small, strongly linked teams that work interdisciplinarily. In addition, interdisciplinary researchers should receive an elaborate training for the field they are collaborating with. Then the methods that are used to design solutions for different problems should transgress disciplinary bounds, in order to allow re-use of methods across fields of research.
Similarly to the situation when travelers have to adapt to local customs, all involved parties need to compromise. The common vocabulary needs to be found and the various perspectives and the different knowledge need to be understood. Only then one can start to discover where and how both sides can benefit from each other or how they can join forces to design novel methods for hybrid societies.
5. Conclusion
We have identified three primary challenges of designing hybrid societies: formalization, system design, and interdisciplinarity. All of them require a lot of attention and a major effort to be overcome. However, a generic formalization approach and efficient interdisciplinary collaborations shall create synergies and enable us to re-use methods at intersections between disciplines. An appropriate system design approach would enable us to quickly deploy safe, reliable, and stable systems in hardware.
Author Contributions
HH and YK wrote the paper and organized the overall writing process. All other authors contributed about equally to the writing process.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer MP declared a shared affiliation, though no other collaboration, with one of the authors (AZ) to the handling Editor, who ensured that the process nevertheless met the standards of a fair and objective review.
Acknowledgments
This work was partially supported by the European Union’s Horizon 2020 research and innovation program under the FET grant agreement “flora robotica,” no. 640959 and the ERC Advanced Grant EPNet (340828). EF acknowledges support from the Fund for Scientific Research (FWO), Flanders, Belgium. RR acknowledges support from EPSRC and the Department of Electronics, University of York, UK. AZ acknowledges support from the Slovenian Research Agency (ARRS, programme P2-0041: Computer Systems, Methodologies, and Intelligent Services).
References
Abelson, H., Allen, D., Coore, D., Hanson, C., Homsy, G., Knight, T., et al. (2000). Amorphous computing. Commun. ACM 43, 74–82. doi: 10.1145/332833.332842
Albert, R., Jeong, H., and Barabási, A.-L. (2000). Error and attack tolerance of complex networks. Nature 406, 378–382. doi:10.1038/35019019
Alexander, J. C., Giesen, B., Münch, R., and Smelser, N. J. (eds) (1987). The Micro-Macro Link. Berkeley, CA: University of California Press.
André, J.-B. (2014). Mechanistic constraints and the unlikely evolution of reciprocal cooperation. J. Evol. Biol. 27, 784–795. doi:10.1111/jeb.12351
Anshakov, O. M., and Gergely, T. (2010). Cognitive Reasoning: A Formal Approach. Berlin, Heidelberg: Springer Science & Business Media.
Ashby, W. (1947). Principles of the self-organizing dynamic system. J. Gen. Psychol. 37, 125–128. doi:10.1080/00221309.1947.9918144
Attanasi, A., Cavagna, A., Del Castello, L., Giardina, I., Grigera, T. S., Jelić, A., et al. (2014). Information transfer and behavioural inertia in starling flocks. Nat. Phys. 10, 691–696. doi:10.1038/nphys3035
Barabási, A.-L., and Albert, R. (1999). Emergence of scaling in random networks. Science 286, 509. doi:10.1126/science.286.5439.509
Barabási, A.-L., Albert, R., and Jeong, H. (1999). Mean-field theory for scale-free random networks. Physica A 272, 173–187. doi:10.1016/S0378-4371(99)00291-5
Baxter, G., and Sommerville, I. (2010). Socio-technical systems: from design methods to systems engineering. Interact. Comput. 23, 4–17. doi:10.1016/j.intcom.2010.07.003
Beal, J., and Bachrach, J. (2006). Infrastructure for engineered emergence on sensor/actuator networks. IEEE Intell. Syst. 21, 10–19. doi:10.1109/MIS.2006.29
Beni, G. (2005). “From swarm intelligence to swarm robotics,” in Swarm Robotics – SAB 2004 International Workshop, Volume 3342 of LNCS, eds E. Şahin and W. M. Spears (Santa Monica, CA: Springer-Verlag), 1–9.
Bettstetter, C. (2004). On the connectivity of Ad Hoc networks. Comput. J. 47, 432–447. doi:10.1093/comjnl/47.4.432
Boerkoel, J. C. Jr., and Durfee, E. H. (2013). Distributed reasoning for multiagent simple temporal problems. J. Artif. Intell. Res. 47, 95–156. doi:10.1613/jair.3840
Bonabeau, E., Dorigo, M., and Theraulaz, G. (1999). Swarm Intelligence: From Natural to Artificial Systems. New York, NY: Oxford Univ. Press.
Brambilla, M., Dorigo, M., and Birattari, M. (2014). Formal Methods for the Design and Analysis of Robot Swarms. Ph.D. thesis, Universite Libre de Bruxelles, Berlin, Heidelberg.
Brambilla, M., Ferrante, E., Birattari, M., and Dorigo, M. (2013). Swarm robotics: a review from the swarm engineering perspective. Swarm Intell. 7, 1–41. doi:10.1007/s11721-012-0075-2
Bredeche, N., and Montanier, J.-M. (2010). “Environment-driven embodied evolution in a population of autonomous agents,” in Parallel Problem Solving from Nature, PPSN XI, eds R. Schaefer, C. Cotta, J. Kołodziej, and G. Rudolph (Berlin, Heidelberg: Springer), 290–299.
Buhl, J., Sumpter, D. J. T., Couzin, I. D., Hale, J. J., Despland, E., Miller, E. R., et al. (2006). From disorder to order in marching locusts. Science 312, 1402–1406. doi:10.1126/science.1125142
Camazine, S., Deneubourg, J.-L., Franks, N. R., Sneyd, J., Theraulaz, G., and Bonabeau, E. (2001). Self-Organizing Biological Systems. Princeton, NJ: Princeton University Press.
Castro, L. (2007). Fundamentals of natural computing: an overview. Phys. Life Rev. 4, 1–36. doi:10.1016/j.plrev.2006.10.002
Cavagna, A., Cimarelli, A., Giardina, I., Parisi, G., Santagati, R., Stefanini, F., et al. (2010). Scale-free correlations in starling flocks. Proc. Natl. Acad. Sci. 107, 11865–11870. doi:10.1073/pnas.1005766107
Correll, N., Cianci, C., Raemy, X., and Martinoli, A. (2006). “Self-organized embedded sensor/actuator networks for “smart” turbines,” in IEEE/RSJ International Conference on Intelligent Robots and Systems Workshop on Network Robot System: Toward Intelligent Robotic Systems Integrated with Environments (Los Alamitos, CA: IEEE Press).
Crucitti, P., Latora, V., Marchiori, M., and Rapisarda, A. (2003). Efficiency of scale-free networks: error and attack tolerance. Physica A 320, 622–642. doi:10.1016/S0378-4371(02)01545-5
Cully, A., Clune, J., Tarapore, D., and Mouret, J.-B. (2015). Robots that can adapt like animals. Nature 521, 503–507. doi:10.1038/nature14422
Dorigo, M., and Caro, G. D. (1999). “Ant colony optimization: a new meta-heuristic,” in Proceedings of the 1999 Congress on Evolutionary Computation (CEC’99), eds P. J. Angeline, Z. Michalewicz, M. Schoenauer, X. Yao, and A. Zalzala (Piscataway, NJ: IEEE Press), 1470–1477.
Dorigo, M., Floreano, D., Gambardella, L. M., Mondada, F., Nolfi, S., Baaboura, T., et al. (2013). Swarmanoid: a novel concept for the study of heterogeneous robotic swarms. IEEE Robot. Autom. Mag. 20, 60–71. doi:10.1109/MRA.2013.2252996
D’Orsogna, M. R., and Perc, M. (2015). Statistical physics of crime: a review. Phys. Life Rev. 12, 1–21. doi:10.1016/j.plrev.2014.11.001
Edelstein-Keshet, L. (2001). “Mathematical models of swarming and social aggregation,” in Proceedings of the 2001 International Symposium on Nonlinear Theory and Its Applications (Miyagi), 1–7.
Eiben, A. (2014). Grand challenges for evolutionary robotics. Front. Robot. AI 1:4. doi:10.3389/frobt.2014.00004
Galam, S., and Moscovici, S. (1991). Towards a theory of collective phenomena: consensus and attitude changes in groups. Eur. J. Soc. Psychol. 21, 49–74. doi:10.1002/ejsp.2420210105
Grimmett, G. (1999). Percolation, Volume 321 of Grundlehren der mathematischen Wissenschaften. Berlin: Springer.
Halloy, J., Mondada, F., Kernbach, S., and Schmickl, T. (2013). “Towards bio-hybrid systems made of social animals and robots,” in Biomimetic and Biohybrid Systems, Volume 8064 of LNCS, eds N. F. Lepora, A. Mura, H. G. Krapp, P. F. Verschure, and T. J. Prescott (Berlin, Heidelberg: Springer), 384–386.
Hamann, H., Valentini, G., Khaluf, Y., and Dorigo, M. (2014). “Derivation of a micro-macro link for collective decision-making systems: Uncover network features based on drift measurements,” in The International Conference on Parallel Problem Solving from Nature (PPSN 2014), Volume 8672 of LNCS, ed. T. Bartz-Beielstein (Berlin, Heidelberg: Springer), 181–190.
Hamann, H., Wahby, M., Schmickl, T., Zahadat, P., Hofstadler, D., Støy, K., et al. (2015). “Flora robotica – mixed societies of symbiotic robot-plant bio-hybrids,” in Proceedings of IEEE Symposium on Computational Intelligence (IEEE SSCI 2015) (Piscataway, NJ: IEEE), 1102–1109.
Hamann, H., and Wörn, H. (2008). A framework of space-time continuous models for algorithm design in swarm robotics. Swarm Intell. 2, 209–239. doi:10.1007/s11721-008-0015-3
Hegselmann, R., and Krause, U. (2002). Opinion dynamics and bounded confidence models, analysis, and simulation. Journal of Artifical Societies and Social Simulation 5, 1–24.
Helbing, D., Brockmann, D., Chadefaux, T., Donnay, K., Blanke, U., Woolley-Meza, O., et al. (2015). Saving human lives: what complexity science and information systems can contribute. J. Stat. Phys. 158, 735–781. doi:10.1007/s10955-014-1024-9
Heylighen, F. (2016). Stigmergy as a universal coordination mechanism I: definition and components. Cogn. Syst. Res. 38, 4–13. doi:10.1016/j.cogsys.2015.12.002
Hoare, C. A. R. (1978). Communicating sequential processes. Commun. ACM 21, 666–677. doi:10.1145/359576.359585
Holme, P., and Saramäki, J. (2012). Temporal networks. Phys. Rep. 519, 97–125. doi:10.1016/j.physrep.2012.03.001
Ismail, A. R., and Timmis, J. (2010). “Towards self-healing swarm robotic systems inspired by granuloma formation,” in Engineering of Complex Computer Systems (ICECCS), 2010 15th IEEE International Conference (Piscataway, NJ: IEEE), 313–314.
Jones, A. J. I., Artikis, A., and Pitt, J. (2013). The design of intelligent socio-technical systems. Artif. Intell. Rev. 39, 5–20. doi:10.1007/s10462-012-9387-2
Kaelbling, L. P., Littman, M. L., and Moore, A. W. (1996). Reinforcement learning: a survey. J. Artif. Intell. Res. 4, 237–285.
Koos, S., Mouret, J.-B., and Doncieux, S. (2013). The transferability approach: crossing the reality gap in evolutionary robotics. IEEE Trans. Evol. Comput. 17, 122–145. doi:10.1109/TEVC.2012.2185849
Lerman, K., Martinoli, A., and Galstyan, A. (2005). “A review of probabilistic macroscopic models for swarm robotic systems,” in Swarm Robotics, eds E. Sahin and W. M. Spears (Berlin, Heidelberg: Springer), 143–152.
Levi, P., and Kernbach, S. (eds) (2010). Symbiotic Multi-Robot Organisms: Reliability, Adaptability, Evolution. Berlin, Heidelberg: Springer.
Mahendra Rajah, P., Prokopenko, M., Wang, P., and Price, D. (2005). “Towards adaptive clustering in self-monitoring multi-agent networks,” in Knowledge-Based Intelligent Information and Engineering Systems: 9th International Conference, KES 2005, Melbourne, Australia, September 14–16, 2005, Proceedings, Part II, eds R. Khosla, R. J. Howlett, and L. C. Jain (Berlin, Heidelberg: Springer), 796–805.
Marras, S., and Porfiri, M. (2012). Fish and robots swimming together: attraction towards the robot demands biomimetic locomotion. Journal of The Royal Society Interface 9, 1856–1868. doi:10.1098/rsif.2012.0084
Martinoli, A. (1999). Swarm Intelligence in Autonomous Collective Robotics: From Tools to the Analysis and Synthesis of Distributed Control Strategies. Ph.D. thesis, Ecole Polytechnique Fédérale de Lausanne, Lausanne.
Martinoli, A., Easton, K., and Agassounon, W. (2004). Modeling swarm robotic systems: a case study in collaborative distributed manipulation. Int. J. Robot. Res. 23, 415–436. doi:10.1177/0278364904042197
Martinoli, A., Ijspeert, A., and Mondada, F. (1999). Understanding collective aggregation mechanisms: from probabilistic modelling to experiments with real robots. Rob. Auton. Syst. 29, 51–63. doi:10.1016/S0921-8890(99)00038-X
Matarić, M. J. (1993). “Designing emergent behaviors: from local interactions to collective intelligence,” in Proceedings of the Second Int. Conf. on From Animals to Animats 2: simulation of adaptive behavior, eds J.-A. Meyer, H. L. Roitblat, and S. W. Wilson (Cambridge, MA: MIT Press), 432–441.
Matarić, M. J. (1997). “Reinforcement learning in the multi-robot domain,” in Robot Colonies, eds R. C. Arkin and G. Bekey (Berlin, Heidelberg: Springer), 73–83.
Mayer, J., Khairy, K., and Howard, J. (2010). Drawing an elephant with four complex parameters. Am. J. Phys. 78, 648–649. doi:10.1119/1.3254017
McCanne, S., Floyd, S., Fall, K., and Varadhan, K. (1997). Network Simulator – ns-2. Availabe from: http://nsnam.sourceforge.net/wiki/index.php/Main_Page
Ohkubo, J., Shnerb, N., and Kessler, D. A. (2008). Transition phenomena induced by internal noise and quasi-absorbing state. J. Phys. Soc. Jap. 77, 044002. doi:10.1143/JPSJ.77.044002
Okubo, A. (1986). Dynamical aspects of animal grouping: swarms, schools, flocks, and herds. Adv. Biophys. 22, 1–94. doi:10.1016/0065-227X(86)90003-1
Omicini, A., and Viroli, M. (2011). Coordination models and languages: from parallel computing to self-organisation. Knowl. Eng. Rev. 26, 53–59. doi:10.1017/S026988891000041X
Parker, L. E. (2000). “Current state of the art in distributed autonomous mobile robotics,” in Distributed Autonomous Robotic Systems, Vol. 4. eds L. E. Parker, G. Bekey, and J. Barhen (Berlin, Heidelberg: Springer), 3–12.
Payton, D., Daily, M., Estowski, R., Howard, M., and Lee, C. (2001). Pheromone robotics. Auton. Robots 11, 319–324. doi:10.1023/A:1012411712038
Perc, M., and Grigolini, P. (2013). Collective behavior and evolutionary games – an introduction. Chaos Solitons Fractals 56, 1–5. doi:10.1016/j.chaos.2013.06.002
Perc, M., and Szolnoki, A. (2010). Coevolutionary games – a mini review. BioSystems 99, 109–125. doi:10.1016/j.biosystems.2009.10.003
Piraveenan, M., Prokopenko, M., and Hossain, L. (2013a). Percolation centrality: quantifying graph-theoretic impact of nodes during percolation in networks. PLoS ONE 8:e53095. doi:10.1371/journal.pone.0053095
Piraveenan, M., Thedchanamoorthy, G., Uddin, S., and Chung, K. S. K. (2013b). Quantifying topological robustness of networks under sustained targeted attacks. Soc. Netw. Anal. Min. 3, 939–952. doi:10.1007/s13278-013-0118-8
Prokopenko, M. (2014). Grand challenges for computational intelligence. Front. Robot. AI 1:1–3. doi:10.3389/frobt.2014.00002
Prorok, A., Correll, N., and Martinoli, A. (2011). Multi-level spatial models for swarm-robotic systems. Int. J. Robot. Res. 30, 574–589. doi:10.1177/0278364910399521
Schillo, M., Fischer, K., and Klein, C. T. (2000). “The micro-macro link in DAI and sociology,” in Multi-Agent-Based Simulation: Second International Workshop, Boston, MA, USA (MABS 2000), Volume 1979 of LNCS, eds S. Moss and P. Davidsson (Berlin: Springer), 303–317.
Schmickl, T., Bogdan, S., Correia, L., Kernbach, S., Mondada, F., Bodi, M., et al. (2013). “ASSISI: mixing animals with robots in a hybrid society,” in Biomimetic and Biohybrid Systems, Volume 8064 of LNCS, eds N. F. Lepora, A. Mura, H. G. Krapp, P. F. Verschure, and T. J. Prescott (Berlin, Heidelberg: Springer), 441–443.
Schmickl, T., and Hamann, H. (2011). “BEECLUST: A swarm algorithm derived from honeybees,” in Bio-inspired Computing and Communication Networks, ed. Y. Xiao (Boca Raton, FL: CRC Press), 95–137.
Schöttl, F., and Lindemann, U. (2015). Quantifying the complexity of socio-technical systems – a generic, interdisciplinary approach. Proc. Comput. Sci. 44, 1–10. doi:10.1016/j.procs.2015.03.019
Serugendo, G. D. M. S., Irit, M.-P., and Karageorgos, A. (2006). Self-organisation and emergence in mas: an overview. Informatica 30, 45–54.
Smirnov, A., Levashova, T., Shilov, N., and Sandkuhl, K. (2014). “Ontology for cyber-physical-social systems self-organisation,” in Open Innovations Association (FRUCT16), 2014 16th Conference (Piscataway, N J: IEEE), 101–107.
Stepney, S. (2007). “Chapter 12: embodiment,” in In Silico Immunology, eds D. Flower and J. Timmis (Berlin: Springer), 265–288.
Stone, P., and Veloso, M. (2000). Multiagent systems: a survey from a machine learning perspective. Auton. Robots 8, 345–383. doi:10.1023/A:1008942012299
Valentini, G., Hamann, H., and Dorigo, M. (2014). “Self-organized collective decision making: the weighted voter model,” in Proceedings of the 13th Int. Conf. on Autonomous Agents and Multiagent Systems, AAMAS ’14, eds A. Lomuscio, P. Scerri, A. Bazzan, and M. Huhns (Richland, SC: International Foundation for Autonomous Agents and Multiagent Systems), 45–52.
Vicsek, T., Czirók, A., Ben-Jacob, E., Cohen, I., and Shochet, O. (1995). Novel type of phase transition in a system of self-driven particles. Phys. Rev. Lett. 6, 1226–1229. doi:10.1103/PhysRevLett.75.1226
Wario, F., Wild, B., Couvillon, M. J., Rojas, R., and Landgraf, T. (2015). Automatic methods for long-term tracking and the detection and decoding of communication dances in honeybees. Front. Ecol. Evol. 3:103. doi:10.3389/fevo.2015.00103
Watson, R. A., Ficici, S. G., and Pollack, J. B. (2002). Embodied evolution: distributing an evolutionary algorithm in a population of robots. Rob. Auton. Syst. 39, 1–18. doi:10.1016/S0921-8890(02)00170-7
Weiß, G. (1996). “Adaptation and learning in multi-agent systems: some remarks and a bibliography,” in Adaption and Learning in Multi-Agent Systems, Volume 1042 of LNCS, eds G. Weiß and S. Sen (New York City, NY: Springer), 1–21. doi:10.1007/3-540-60923-7_16
Winfield, A. F. T., Sav, J., Fernández-Gago, M.-C., Dixon, C., and Fisher, M. (2005). On formal specification of emergent behaviours in swarm robotic systems. International Journal of Advanced Robotic Systems 2, 363–370. doi:10.5772/5769
Witten, J. T. A., and Sander, L. M. (1981). Diffusion-limited aggregation, a kinetic critical phenomenon. Phys. Rev. Lett. 47, 1400–1403. doi:10.1103/PhysRevLett.47.1400
Wolpert, D. H., and Tumer, K. (1999). An Introduction to Collective Intelligence. Technical Report. Handbook of Agent Technology. Moffett Field, CA: AAAI.
Yang, C. N. (1952). The spontaneous magnetization of a two-dimensional Ising model. Phys. Rev. 85, 808–816. doi:10.1103/PhysRev.85.808
Keywords: hybrid society, bio-hybrid, distributed, collective, self-organization, design, interdisciplinarity
Citation: Hamann H, Khaluf Y, Botev J, Divband Soorati M, Ferrante E, Kosak O, Montanier J-M, Mostaghim S, Redpath R, Timmis J, Veenstra F, Wahby M and Zamuda A (2016) Hybrid Societies: Challenges and Perspectives in the Design of Collective Behavior in Self-organizing Systems. Front. Robot. AI 3:14. doi: 10.3389/frobt.2016.00014
Received: 30 January 2016; Accepted: 14 March 2016;
Published: 11 April 2016
Edited by:
Carlos Gershenson, Universidad Nacional Autónoma de México, MexicoReviewed by:
Mahendra Piraveenan, University of Sydney, AustraliaMatjaž Perc, University of Maribor, Slovenia
Copyright: © 2016 Hamann, Khaluf, Botev, Divband Soorati, Ferrante, Kosak, Montanier, Mostaghim, Redpath, Timmis, Veenstra, Wahby and Zamuda. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Heiko Hamann, aGVpa28uaGFtYW5uQHVuaS1wYWRlcmJvcm4uZGU=
 Heiko Hamann
Heiko Hamann Yara Khaluf
Yara Khaluf Jean Botev
Jean Botev Mohammad Divband Soorati
Mohammad Divband Soorati Eliseo Ferrante
Eliseo Ferrante Oliver Kosak
Oliver Kosak Jean-Marc Montanier
Jean-Marc Montanier Sanaz Mostaghim
Sanaz Mostaghim Richard Redpath
Richard Redpath Jon Timmis
Jon Timmis Frank Veenstra
Frank Veenstra Mostafa Wahby
Mostafa Wahby Aleš Zamuda
Aleš Zamuda