Abstract
We present a new package for joint deconvolution of ALMA 12 m, 7 m, and Total Power (TP) data, dubbed "Total Power Map to Visibilities (Tp2vis)". It converts a TP (single-dish) map into visibilities on the Casa platform, which can be input into deconvolvers (e.g., Clean) along with 12 m and 7 m visibilities. The Tp2vis procedure is based primarily on the one discussed in Koda et al. A manual is presented in the Github repository (https://github.com/tp2vis/distribute). Combining data from the different ALMA arrays is a driver for a number of science topics, namely those that probe size scales of extended and compact structures simultaneously (e.g., protostar outflows and environment, AGB stars and planetary nebulae, molecular clouds and cores, and molecular clouds in galaxies). We test Tp2vis using model images, one with a single Gaussian and another that mimics the internal structures of giant molecular clouds. The result shows that the better uv coverage with Tp2vis visibilities clearly helps the deconvolution process and reproduces the model image within errors of only 5% over two orders of magnitude in flux. In the Appendix, we describe how the model image is generated.
1. Introduction
The Atacama Large Millimeter/submillimeter Array (ALMA) consists of three sets of telescopes: two interferometers with 12 m and 7 m dishes and Total Power (TP) 12 m single-dish telescopes. The interferometers alone cannot obtain information on an extended emission distribution. Combined, these three sets can recover structures from small to large scales. This emphasizes the importance of single-dish data in the imaging process. Interferometers collect Fourier components of a 2D brightness distribution in the sky, but cannot obtain full coverage of the uv space (i.e., Fourier space). Hence, the empty part of the uv space has to be filled (or "guessed") in the deconvolution process, with the filled part of the uv space used as a guideline. Convergence is not guaranteed, but a better sampled uv space helps this process. The combination of interferometer and single-dish data provides better uv coverage, thus leading to better imaging results.
The idea of combining interferometry and single-dish data was introduced early (Bajaja & van Albada 1979; Ekers & Rots 1979, who called it "short-spacing corrections"), but in practice the procedure is still under debate. The history and techniques for combination are summarized in Stanimirovic (2002). The techniques can be classified into three general categories: whether the data are combined (1) before, (2) during, or (3) after deconvolution (e.g., Clean). For better uv coverage for deconvolution, (1) and (2) have natural advantages (e.g., Cornwell 1988). Each of these categories can be split into two subcategories: whether the operations are performed (a) in the Fourier domain (uv domain) or (b) in the image domain.
1.1. Combination After Deconvolution
A common technique of the after-deconvolution combination (category 3a) applies low- and high-pass filters to single-dish and cleaned interferometer maps (or images), respectively. The maps are then added in the Fourier domain and transformed back to a final map. It is now called the Feather technique. Several implementations exist (e.g., the Imerge task in Aips; Immerge task in Miriad; Herbstmeier et al. 1996; Weiß et al. 2001). The Feather task7
in Casa is one more recent example. It adopts the low-pass filter,  , and a high-pass filter,
, and a high-pass filter,  , where the Fourier transform (FT) of the TP primary beam
, where the Fourier transform (FT) of the TP primary beam  is used.8
Feather's choice of H(u, v) extends to uv ≈ 0 which interferometer data does not cover. To avoid this, Blagrave et al. (2017) used different filters with non-zero values only where the data exist. Since multiplications (or divisions) in the Fourier domain are equivalent to convolutions (deconvolutions) in the image domain, it is possible to implement the same technique both in the Fourier and image domains. Faridani et al. (2018) implemented the Feather technique in the image domain (category 3b).
is used.8
Feather's choice of H(u, v) extends to uv ≈ 0 which interferometer data does not cover. To avoid this, Blagrave et al. (2017) used different filters with non-zero values only where the data exist. Since multiplications (or divisions) in the Fourier domain are equivalent to convolutions (deconvolutions) in the image domain, it is possible to implement the same technique both in the Fourier and image domains. Faridani et al. (2018) implemented the Feather technique in the image domain (category 3b).
1.2. Combination During Deconvolution
The TP map can be used as an initial model for deconvolution of interferometer data (category 2a). Practically, such a scheme deconvolves single-dish and interferometer data jointly (Cornwell 1988). The Clean/Tclean tasks in Casa can take a single-dish map as an input. Dirienzo et al. (2015) employed this technique and produced a combined map. They further applied Feather to ensure that the large-scale components precisely represented the TP data.
1.3. Combination Before Deconvolution
Pseudo visibilities can be generated from a single-dish map. They can be added to interferometer visibilities before deconvolution (category 1a; Vogel et al. 1984). Once TP visibilities are generated from the TP map, they are readily fed into existing deconvolvers (e.g., Clean/Tclean). This technique has also been used, though there are some discussions on how to optimize the distribution and weights of the pseudo visibilities (e.g., Rodríguez-Fernández 2008; Kurono et al. 2009; Pety & Rodríguez-Fernández 2010; Koda et al. 2011). For example, Koda et al. (2011) generated a Gaussian visibility distribution and set the visibility weight so that the single-dish primary beam is represented. One of the advantages of pseudo visibilities techniques is that the visibility weight can be easily controlled within single-dish data, as well as with the interferometer data.
The same technique can be implemented in the image domain (category 1b; Stanimirovic et al. 1999). The single-dish and interferometer dirty beams, as well as their maps, are added with a choice of L(u, v) and H(u, v). The combined dirty map can then be deconvolved with the combined dirty beam. This is equivalent to the pseudo visibility techniques, because a FT of a sum of two functions is equal to the sum of the FT of the two functions. The weights can be changed by adjusting L(u, v) and H(u, v). Such implementation is being developed in Casa (U. Rau et al. 2019, in preparation).
1.4. This Work
Tools are needed for the combination of ALMA data in the platform of the Common Astronomy Software Applications (Casa; McMullin et al. 2007). Here, we introduce a new package in Casa that converts ALMA's TP map into pseudo visibilities (dubbed Tp2vis). It generates visibilities as if they were observed by a virtual interferometer with short spacings down to zero spacial frequency. Together with ALMA 12 m+7 m data, the Tp2vis visibilities can be fed into standard deconvolvers for joint deconvolution. The technique follows the one developed by Koda et al. (2011) on the Miriad platform (Sault et al. 1995), but with improvements.
The Tp2vis package provides four functions in the CASA platform. The key function, Tp2vis, generates a CASA measurement set (MS) –visibilities with weights–from a TP map. The weights are calculated based on the root-mean-square (rms) noise from the TP map. This MS is ready for joint deconvolution, though in some cases one may wish to manipulate the weights using the supplementary function, Tp2viswt. An accessory function, tp2vispl, plots the weights of ALMA 12 m, 7 m, and TP visibilities for comparison. Another function, tp2vistweak, attempts to fix the problem of beam-size mismatch in the image space after deconvolution (Section 3.2).
2. The TP2VIS Procedure
The Tp2vis function takes a sky brightness distribution (TP map) and simulates observations with a virtual interferometer (defined below). Figure 1 shows the flowchart of steps in the tp2vis function. The details of the steps are in the following subsections. From a top view, the procedure can be separated into three parts. First, it converts the TP map into the sky brightness distribution, which will be observed by the virtual interferometer (steps A and B in the figure). Second, it converts the brightness distribution into visibilities (steps C and D). And third, the weights of the TP visibilities are set so that they represent the rms noise of the original TP map (step E).
Figure 1. Flowchart of the Tp2vis procedure. Tp2vis processes the operations shaded in blue: taking a calibrated TP data cube from CASA, converting it into a set of visibilities (i.e., a measurement set), and passing it to a deconvolution task in CASA. The TP visibilities from Tp2vis can be jointly deconvolved with the ALMA 12 m and 7 m interferometer visibilities.
Download figure:
Standard image High-resolution imageDifferent types of beams are involved in our discussions. For clarity we list the beams in Table 1.
Table 1. Beam Terminology
| Number | Beam Name | Symbol |
|---|---|---|
| 1 | Primary beam of Total Power (TP) telescopes | ΩTP |
| 2 | Primary beam of Virtual Interferometer (VI) telescopes | Ωvir |
| 3 | Dirty beam (output from clean/tclean with niter=0) | Ωdirty |
| Synthesized beam | Ωsyn | |
| Deconvolution beam | Ωdec | |
| Point-spread function | Ωpsf | |
| 4 | CLEAN beam (typically derived from Gaussian fit to Ωdirty) | Ωclean |
| Convolution beam | Ωconv | |
| Restoring beam | Ωres | |
Note. Horizontal lines separate different beams. The third and forth beams have a few names:  , and
, and  .
.
Download table as: ASCIITypeset image
2.1. Step A: Deconvolution with TP Beam ΩTP
This step is a preparation for the virtual interferometer observations. When the TP telescopes observe the sky, the TP telescope beam, ΩTP, is convolved with the brightness distribution in the sky. Therefore, the first step is to deconvolve the TP map with ΩTP and to obtain the true sky brightness distribution in Jy/beam.
We approximate ΩTP with a Gaussian with a FWHM of 56.6'' at 115.2 GHz. We assume that it scales linearly with 1/frequency.
2.2. Step B: Apply Virtual Primary Beam Ωvir
When an interferometer observes the sky, the brightness distribution is attenuated by its primary beam (PB). Hence, the sky brightness distribution from Step A is multiplied by the PB pattern of the virtual interferometer (Ωvir). In case of mosaic observations, this must be done at each pointing position.
In our virtual observations, the coordinates of pointing centers can be set arbitrarily within the TP map. We typically take them from the ALMA 12 m data, so that the 12 m and TP visibilities have the same sky coverage. The pointing coordinates are listed in an ASCII file and passed to the Tp2vis function with the "ptg =" argument.
2.3. Step C: Generate Gaussian Visibility Distribution
In parallel with steps A and B, a visibility distribution for the virtual observations (hence a MS) is prepared. We generate a two-dimensional Gaussian distribution of visibilities in the uv space, so that its Fourier transformation, i.e., the synthesized beam Ωsyn, reproduces the Gaussian beam of the TP telescopes (ΩTP). Adopting a constant weight for all TP visibilities (Section 4), this distribution would represent the sensitivity distribution within the TP beam. The width of the Gaussian visibility distribution is determined from those of the Gaussian beam. The standard deviations of the Gaussian beam in the sky σ and the Gaussian distribution in the uv space σF are related as σF = 1/(2πσ).
The full width at half maximum (FWHM) is calculated as  (≈2.355σ). For a FWHM of 56.6'', σ = 2.74 × 10−4 radian and σF = 580λ, where λ is the wavelength.
(≈2.355σ). For a FWHM of 56.6'', σ = 2.74 × 10−4 radian and σF = 580λ, where λ is the wavelength.
2.4. Step D: Fill Visibility Amplitudes and Phases
We already have the sky brightness distribution with the PB of the virtual interferometer applied (from step B), and the Gaussian visibility distribution in the uv space (step C). Now, the sky brightness distribution is Fourier-transformed into the uv space. The amplitude and phase of the transformation are then sampled at the visibility positions, which fill the AMPLITUDE and PHASE columns of the visibilities in the MS.
These visibilities are already internally consistent. The Clean/Tclean tasks with natural weighting produce a synthesized beam Ωsyn roughly equal to the TP telescope beam ΩTP. The brightness distribution also reproduces the observed TP brightness distribution.
2.5. Step E: Set Weights of TP Visibilities
The Tp2vis function sets visibility weights according to the rms noise in the TP map. The rms value is set manually by the "rms =" argument [in units of Jy/beam of the TP map]. [Note that in the current implementation, the rms is set by hand, because it is not always trivial to find emission-free channels using an algorithm.] The rms is converted to the weight of individual visibilities. The equation for this conversion is in Section 4. The sensitivity-based weight is a proper representation of the quality of the TP data and is the default of Tp2vis.
In the history of radio interferometry, the weights are often manipulated. The most common examples are the uniform, robust/briggs, or taper weighting schemes. There is no reason not to manipulate them in some other ways—for example, to match the weights of TP visibilities with those of ALMA 12 m and 7 m data (their sensitivities may not match when one works on archival data). The supplementary tp2viswt function provides several options to manipulate the weights. An accessory tp2vispl function plots the weight distributions of ALMA 12 m, 7 m, and TP visibilities for comparison, so that users can decide how the TP visibilities need to be weighted with respect to 12 m and 7 m data.
3. Beam Disparity and Flux Problem
Imaging of interferometer data involves several different beams. Some of them are often referred with different names by different researchers or in different circumstances. This is very confusing. Furthermore, their differences cause a more practical issue in flux conservation in the process of imaging. In order to discuss the issue, we first explain the beams. For Tp2vis we use four different beams (Table 1).
The first two beams were used in Section 2: the primary beam of the TP telescopes (ΩTP) and that of the virtual interferometer (Ωvir). The third and fourth beams are from visibilities, i.e., a synthesized beam (Ωsyn) and convolution beam (Ωconv). The Ωsyn is also called the dirty beam (Ωdirty), deconvolution beam (Ωdec), or point-spread function (Ωpsf). The Ωconv is also called the clean beam (Ωclean) or restoring beam (Ωres). For discussions in later sections, we give more precise definitions of Ωsyn and Ωconv in Section 3.1.
Jörsater & van Moorsel (1995) extensively discussed the problem of flux conservation when there is a disparity between the areas of Ωsyn and Ωconv. The problem becomes more apparent when the TP visibilities are included (Section 3.2). We discuss two techniques to resolve/mitigate this problem: by adjusting the weights of the TP visibilities (Section 4.2) and/or by scaling the residual map (Section 5).
Note that we use the symbols, Ωsyn and Ωconv, to represent the synthesized and convolution beams, respectively, but also to denote their areas.
3.1. The Synthesized and Convolution Beams
The synthesized beam Ωsyn is determined by the distributions of visibility weights in uv space [Note:  ]. Its 2D pattern, B(l, m), is a Fourier transformation of the weight distribution W(u, v). With the normalization of
]. Its 2D pattern, B(l, m), is a Fourier transformation of the weight distribution W(u, v). With the normalization of  ,
,
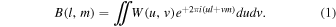
The area of Ωsyn is the beam solid angle and is given as an integration over space,
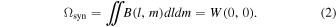
It depends only on W(0, 0), the weight at (u, v) = (0, 0). Therefore, only the weight of the TP visibility matters, because the interferometer data have zero weight at (u, v) = (0, 0). Therefore,  when ALMA 12 m, 7 m, and TP are combined.
when ALMA 12 m, 7 m, and TP are combined.
The convolution beam Ωconv is typically defined by a Gaussian fit to the central peak in the B(l, m) pattern [Note:  ]. Hence, it depends on the full weight distribution, W(u, v); but in practice, the outer, long-baseline part of the visibility weight distribution is often the determining factor.
]. Hence, it depends on the full weight distribution, W(u, v); but in practice, the outer, long-baseline part of the visibility weight distribution is often the determining factor.
In summary, Ωsyn is set at the center of the uv space, while Ωconv is determined mainly by the outer part.
3.2. Beam Disparity and Flux Problem
For simplicity, we use Clean as an example here, but it applies to other deconvolvers as well. The Clean task iteratively finds peaks in a dirty map, whose brightness units are Jy/Ωsyn. In each iteration Clean identifies a peak in a dirty map, fits the 2D pattern of Ωsyn to the peak and obtains its position and amplitude, subtracts it from the dirty map, and puts a δ-function at that position in a clean-component map. The Clean task then convolves the clean-component map with Ωconv to produce a model map. The model map has brightness units of Jy/Ωconv. Typically, Clean is not perfect and leaves emission in a residual map. The unit of the residual map remains Jy/Ωsyn. Clean naively adds the model and residual maps to produce a final map, whose unit is often denoted as Jy/beam. For the "beam" in the denominator, Ωconv is typically adopted. Therefore,
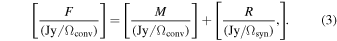
where F, M, and R stand for the final, model, and residual maps, respectively.
The areas and patterns of Ωsyn and Ωconv could be very different, as they depend on different parts of the weight distribution in the uv space (Section 3.1). In particular, if their areas are not equal, Ωsyn  Ωconv, the brightness of R in Equation (3) is calculated incorrectly. For example, if Ωsyn ≫ Ωconv, the brightness in R is overestimated by Ωsyn/Ωconv (≫1), leading to an overestimation of flux in F. This happens when the ALMA 12 m, 7 m, and TP visibilities are combined. In theory, the R could be zero if we could clean down to zero flux, but in practice, it is nearly impossible to get there, as the map to be cleaned has noise.
Ωconv, the brightness of R in Equation (3) is calculated incorrectly. For example, if Ωsyn ≫ Ωconv, the brightness in R is overestimated by Ωsyn/Ωconv (≫1), leading to an overestimation of flux in F. This happens when the ALMA 12 m, 7 m, and TP visibilities are combined. In theory, the R could be zero if we could clean down to zero flux, but in practice, it is nearly impossible to get there, as the map to be cleaned has noise.
In case of Ωsyn ≪ Ωconv, the brightness in R is underestimated. The impact of this on F may not be as noticeable as in the opposite case, as R typically has much less flux than M. This happens when the 12 m and 7 m visibilities are imaged without TP, because  (hence, ≪Ωconv). This flux problem did not attract much attention in the past, as single-dish data were typically not included.
(hence, ≪Ωconv). This flux problem did not attract much attention in the past, as single-dish data were typically not included.
4. Weights
The optimal weighting scheme for TP visibilities is a topic of debate. Tp2vis provides some implementations of weighting schemes, as well as providing a framework for testing other schemes in the future. It has been very common to manipulate visibility weights in the history of radio interferometry. For example, the natural weighting scheme takes the sensitivities of individual visibilities measured during observations, and uses them as a weight distribution in the uv space. The uniform weighting scheme takes a binary approach, setting the weights to 1 at the positions in the uv space where visibilities exist and 0 for the rest, independent of sensitivities. The robust/briggs weighting connects the natural and uniform weightings and transforms one from the other seamlessly by adjusting the single "robust" parameter. Of course, one could come up with other arbitrary weighting schemes to accomplish particular scientific goals. No matter what weights are used, the final map should be usable for scientific applications, as long as the same weights are used consistently for both map and beam by deconvolvers.
Our main function, Tp2vis, sets the weights so that their sum represents the rms noise of the original TP map. This is the default in Tp2vis. In case that users wish to manipulate the weights in other ways, the supplementary function, Tp2viswt, provides options to manipulate the weights. Currently, it has five modes:
- 1.mode="statistics": output statistics of the current weights in MS(s).
- 2.mode="constant", value=: set the weights of all visibilities to a constant specified by "value=".
- 3.mode="multiply", value=: multiply the current weights by a constant specified by "value=".
- 4.mode="rms", value=: use the sensitivity-based weight for all visibilities (Section 4.1). An rms value from TP map should be set with "value=". This is the default weights in Tp2vis.
- 5.mode="beam": use the beam size-based weight for all the TP visibilities (Section 4.2).
In what follows, we discuss two provisional approaches to optimizing the weight, one based on the rms noise (Section 4.1) and another that matches the areas of synthesized and convolution beams (Section 4.2). This beam matching is important to ensure flux conservation in deconvolution, and we will revisit this in Section 5. Tp2vis adjusts the weight in the uv space, but the same can be done in the image domain (Section 4.3).
4.1. The Sensitivity-based Weight
One of the most intuitive weighting schemes is the one that represents the quality of TP data, namely the root-mean-square (rms) noise of the TP map. This is the default weighting scheme used by the Tp2vis function, and the Tp2viswt function with the mode = "rms" can set the weights to the sensitivity-based one. This section explains the calculation of the sensitivity-based weights in Tp2vis. Section 4.1.1 discusses the conversion of the rms noise of a TP map into the weights of individual visibilities. For a joint deconvolution, the weights of 12 m, 7 m, and TP data should be set consistently. Hence, Section 4.1.2 shows the corresponding weights of 12 m and 7 m data. [Note that CASA version 5 uses this definition of 12 m and 7 m weights by default, improving upon prior CASA versions.]
This sensitivity-based weighting is equivalent to the conventional "natural" weighting. For interferometer data, additional manipulations, such as "robust/briggs" or "uniform" weighting schemes, are often applied on top of the sensitivity-based weights. Such manipulations can also be applied to the sensitivity-based weights from Tp2vis. For simplicity, however, the discussions in this section will focus on the sensitivity-based (natural) weights.
4.1.1. Weights for TP Visibilities
With the natural weighting, the sensitivity of a map, or the rms noise of the image ( ), is a simple summation over all visibility sensitivities (
), is a simple summation over all visibility sensitivities ( ),
),
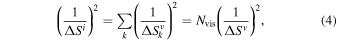
where Nvis is the number of visibilities. All visibilities are assumed to have the same sensitivity ( ), and a single rms value is assumed for the map. Hence, the weight of each TP visibility is
), and a single rms value is assumed for the map. Hence, the weight of each TP visibility is
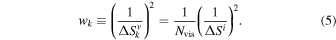
4.1.2. Corresponding Weights for 12 m and 7 m Visibilities
For consistency, the 12 m and 7 m data should also use the sensitivity-based weights. The sensitivity for a single visibility k between antennas i and j is given by
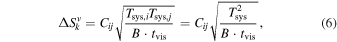
where  ,
,  , and B,
, and B,  are the system temperatures of i and j, bandwidth, and integration time of the visibility, respectively (Taylor et al. 1999; Thompson et al. 2007). For simplicity, we assume
are the system temperatures of i and j, bandwidth, and integration time of the visibility, respectively (Taylor et al. 1999; Thompson et al. 2007). For simplicity, we assume  . The coefficient Cij is
. The coefficient Cij is
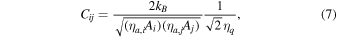
where  ,
,  , Ai, Aj, and
, Ai, Aj, and  are the aperture efficiencies and areas of antennas i and j, and the quantum efficiency of correlator, respectively. With the natural weighting, the rms sensitivity of final map is
are the aperture efficiencies and areas of antennas i and j, and the quantum efficiency of correlator, respectively. With the natural weighting, the rms sensitivity of final map is
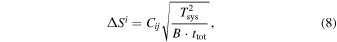
where ttot is the total integration time  . The weights of 12 m and 7 m visibilities should be set to
. The weights of 12 m and 7 m visibilities should be set to  with Equation (6).
with Equation (6).
4.1.3. For Internal Consistency
This subsection is not necessary in practice, but is included for consistency among all data columns in the MS. It might become important in future versions of CASA. Tp2vis fills the WEIGHT and SIGMA columns. Only the WEIGHT column is used by Clean/Tclean in Casa—currently, other columns do not matter. However, one could also make the EXPOSURE column (i.e., integration time of each visibility) consistent.
The sensitivity equations for TP, corresponding to Equations (6), (8), and (7), are
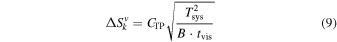
and
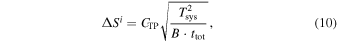
where
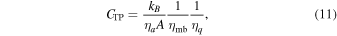
and ηmb is the main beam efficiency of the TP antennas. Tsys,  , and B are determined by observation. With Equation (10) we can derive
, and B are determined by observation. With Equation (10) we can derive  , using Tsys and
, using Tsys and  from MS and TP maps, respectively. Equations (5), (9), and (10) give
from MS and TP maps, respectively. Equations (5), (9), and (10) give  .
.
4.2. The Beam Size-based Weight
Section 3.2 discussed the problem in flux due to the disparity between the areas of Ωsyn and Ωconv. The beam size-based weighting scheme discussed here is an attempt to adjust the weights of TP visibilities to equalize their areas. Note again that we use the symbols, Ωsyn and Ωconv, to represent the areas of the beams as well as to refer the beams themselves.
4.2.1. The Synthesized and Convolution Beams from Combined INT+TP Visibilities
The pattern of the synthesized beam  , denoted by B(l, m), is given by Equation (1). The weight is normalized as
, denoted by B(l, m), is given by Equation (1). The weight is normalized as  . For interferometers (hereafter INT; e.g., ALMA 12 m and 7m) and TP, the synthesized beam patterns,
. For interferometers (hereafter INT; e.g., ALMA 12 m and 7m) and TP, the synthesized beam patterns,  and
and  , are derived with their normalized weights,
, are derived with their normalized weights,  and
and  , respectively.
, respectively.
By defining a relative weight parameter β, a combined weight distribution of INT and TP can be expressed as
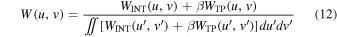
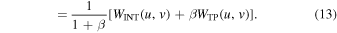
The corresponding synthesized beam pattern is
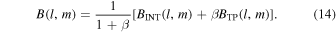
The area of the synthesized beam is derived from Equations (2) (13),
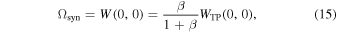
where we used  since INT has no contribution at zero spacing. Note that
since INT has no contribution at zero spacing. Note that  is equal to the area of the synthesized beam of TP visibilities.
is equal to the area of the synthesized beam of TP visibilities.
The convolution beam  is typically derived by a 2D Gaussian fit to the central peak in
is typically derived by a 2D Gaussian fit to the central peak in  . Using the major and minor axis diameters, bmaj and bmin, from the fit, the area of Ωconv is
. Using the major and minor axis diameters, bmaj and bmin, from the fit, the area of Ωconv is
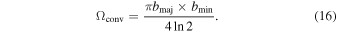
4.2.2. Setting Up Weights for TP Visibilities
This weighting scheme attempts to achieve  . Equation (15) gives β as
. Equation (15) gives β as
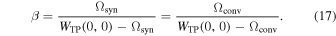
WTP(0, 0) is equal to the area of the synthesized beam of TP visibilities alone, which, by construction, is the same as that of the Gaussian primary beam of the TP antennas. Hence,
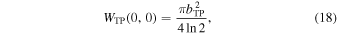
using the FWHM beam size of the TP antennas,  . The Ωconv should be calculated from INT+TP visibilities, but in practice it depends primarily –and almost solely–on the longest baselines. Hence, for simplicity, we derive Ωconv from INT visibilities alone. We can calculate β from Equations (17), (18), and (16) for INT.
. The Ωconv should be calculated from INT+TP visibilities, but in practice it depends primarily –and almost solely–on the longest baselines. Hence, for simplicity, we derive Ωconv from INT visibilities alone. We can calculate β from Equations (17), (18), and (16) for INT.
Using β, we adjust the TP visibility weight distribution from WTP to βWTP, by scaling the weights of individual visibilities ( and
and  for INT and TP visibilities in MSs, respectively).
for INT and TP visibilities in MSs, respectively).
For the following, we use the notation  for an unnormalized weight distribution. The ratio of the two terms in the numerator of Equation (13) is
for an unnormalized weight distribution. The ratio of the two terms in the numerator of Equation (13) is
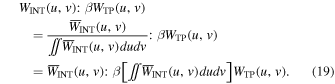
This transformation converts the normalized  into the unnormalized
into the unnormalized  , which is what is delivered from the ALMA observatory. The term to the right of the ratio mark gives the corresponding normalization for the weights of TP visibilities. When the natural weighting is used, the unnormalized
, which is what is delivered from the ALMA observatory. The term to the right of the ratio mark gives the corresponding normalization for the weights of TP visibilities. When the natural weighting is used, the unnormalized  and
and  are related as
are related as  . Thus, for the normalized
. Thus, for the normalized  , we set
, we set  . Also, the term in the bracket is simply,
. Also, the term in the bracket is simply,  . Therefore,
. Therefore,
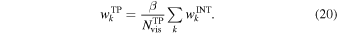
This weight would satisfy  when the INT and TP visibilities are combined.
when the INT and TP visibilities are combined.
4.3. Notes on Visibility and Weight Distributions
The weight distribution of TP visibilities can be controlled, either by changing the distribution of TP visibilities in uv space, and/or by adjusting the weights of individual visibilities. Tp2vis takes the former approach: generating a Gaussian visibility distribution with a constant weight for all the visibilities.
The latter approach could be useful in future. For example, one could generates a grid distribution, instead of the Gaussian distribution, and change the visibility weights as a function of uv distance so that the weight distribution follows a Gaussian. This way, one could avoid shot noise due to the randomly-distributed discrete visibilities. In the end, the Clean task would put the visibilities onto a grid. If the grid spacing is controlled consistently between Tp2vis and Clean, we can test grid-based approaches in future. Of course, the weight distribution can be realized on a grid without visibilities. An implementation of this would require an update of the Clean/Tclean task in Casa (U. Rau 2018, private communication).
5. The Residual Scaling
The flux problem in Section 3.2 is due to the disparity between the areas of Ωsyn and Ωconv in Equation (3). The residual part of the final image from Clean is added incorrectly with inconsistent units of brightness. To circumvent this inconsistency, we could rescale the residual map by a factor of  and add it to the model map to generate a new final map. The tp2vistweak function does this operation.9
and add it to the model map to generate a new final map. The tp2vistweak function does this operation.9
In theory,  can be calculated with the images of Ωsyn from Clean, but it turns out not to be that simple. The estimation of
can be calculated with the images of Ωsyn from Clean, but it turns out not to be that simple. The estimation of  depends on how the visibilities are gridded in the imaging process. The integration of the synthesized beam,
depends on how the visibilities are gridded in the imaging process. The integration of the synthesized beam,  , requires an unrealistically large image size as its tiny responses at the far outskirts add up and their area is cumulatively large.
, requires an unrealistically large image size as its tiny responses at the far outskirts add up and their area is cumulatively large.
Instead, Jörsater & van Moorsel (1995) suggested a more practical approach by taking advantage of detected emissions. In parallel to Equation (3), we can write a similar equation for the dirty map D,
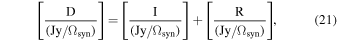
where I is a clean-component map, i.e., a map of the emissions that will be identified by Clean. We should note that the brightness unit is Jy/Ωsyn for all terms, and that M and I in Equations (3) and (21) represent exactly the same emissions in different units. The D, F, and R are given by Clean. We can calculate the scaling factor as
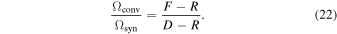
We multiply the R map by this factor and add it to M to construct a new F as in Equation (3), but with a consistent brightness unit (consistent beam areas). This residual scaling method is included in the Aips task Imager and was used recently, e.g., by Walter et al. (2008) and Ianjamasimanana et al. (2017).
In principle, this method can be applied on a pixel-by-pixel basis, as long as the emissions are significantly detected across the map. In practice, this is not always the case. In addition, different spillovers of the beam patterns of Ωsyn and Ωconv degrade the accuracy of the calculation on a pixel-by-pixel basis. Hence, Tp2vis integrates the part of map with significant detections and calculates a single beam ratio with Equation (22). Currently, Tp2vis uses a single ratio even for mosaics, which may be modified in the future as the synthesized beam may vary among mosaic fields.
One may wonder why Jörsater & van Moorsel (1995) could apply this technique to pure interferometer data without single-dish. In that case Ωsyn = W(0, 0) = 0, and the denominator of the left-hand side of Equation (22) is apparently zero. The answer lies in the fact that Equation (22) is the ratio of surface brightnesses in units of Jy/beam (see the right-hand side). Both the numerator (i.e., flux) and denominator (beam) of D − R are zero, but their ratio, and hence the surface brightness, has a finite value. Hence, this method is applicable to pure interferometer data as well.
6. Imaging Tests
We test Tp2vis using model images. With their known emission distributions, the model images allow us to evaluate the accuracy of image deconvolution with Tp2vis. We use Casa version 5.4.0–68 and employ the Clean task for imaging. Examples with actual ALMA data are found in the Github repository of Tp2vis, but not in this paper, as they will evolve with future updates of Casa.
6.1. Setup
6.1.1. Model Images
Two model images are used for tests (Figure 2). One is a single Gaussian emission distribution with a standard deviation of 1500 pixels in width (i.e., FWHM of ∼53'' in the definition described below), and another is a pseudo sky image that mimics small to large structures within giant molecular clouds (GMCs), i.e., dense cores and extended emission (see the Appendix). The current Clean/Tclean tasks tend to cause flux divergence near the edge of a mosaic field of view. As a workaround, the emission around the edge is tapered off outward so that it reaches zero at around the ∼80% level of the maximum primary beam coverage (see Section 6.1.4).
Figure 2. Model images with a dimension of 16,3842, corresponding to 4.096'2 with the adopted cell size of 0.015''. The peak flux is scaled to 1. (a) Gaussian model. A single Gaussian at the center of the field of view with a standard deviation of 1,500 pixels (i.e., FWHM ∼ 53''). (b) Pseudo sky model. It mimics small to large structures in GMCs (see the Appendix). The 38 mosaic pointings are plotted with crosses. The 12 m and 7 m beam sizes, i.e., FWHM = 50.6'' and 86.7'' at 115 GHz, are shown around the lower-left pointing for reference. The green lines show the 40% and 80% levels of the peak of the 12m+7m+TP combined primary beam attenuation. Note that panel (a) is in a linear scale, while panel (b) is in a log scale to show the low-level extended emission.
Download figure:
Standard image High-resolution imageBoth images have the same dimensions of 16,3842 and are configured to the same setup, i.e., an image center coordinate of (RA, DEC)=(12h00m00s, −35d00m00s), a cell size of 0.015'' (hence the image size of 4.096'), and a frequency of 115 GHz with a bandwidth of 2 GHz (a single channel). We run the Simobserve task to convert the images into the CASA format with these parameters. The 0.015'' cell size is chosen to include the main structures in a 38-pointing mosaic (Section 6.1.2) and corresponds to baselines of ∼36 km when observed at 115 GHz. Therefore, the images can be properly sampled by all the ALMA configurations including the one with the longest baseline (∼16 km). The flux scale is arbitrary, and only the relative flux with respect to the peak is important in the tests. The peak flux is set to 1 for Figure 2.
6.1.2. Visibilities for 12 m and 7 m Arrays
We employ a 38-pointing mosaic pattern with a 0.4'spacing. This is a slightly finer spacing than the Nyquist sampling of the primary beam of the 12 m array. The coordinates of the 38 mosaic pointings are determined by Simobserve. The same coordinates are used for the 12 m, 7 m, and TP arrays, and we explicitly set the uv coverage to be exactly the same for all the 38 pointings so that the point-spread function (PSF) shape does not vary across the mosaic field except near the edge (see Section 6.1.4).
Figure 2 shows the 38 pointing centers (crosses), the 40 and 80% levels of the 12m+7m-combined primary beam attenuation (green lines), and the 12 m and 7 m beam sizes (white circles) as references. To control the number of visibilities, we adjust total and individual integration times in Simobserve. The weights of visibilities are set separately, so these times affect nothing but the number of visibilities to be generated: the total integration time of each pointing per array configuration is set to 1,000 sec with a 10 sec integration. This results in 100 visibilities per baseline. We use one configuration for the 7 m array ("aca.i.cfg") and four configurations for the 12 m array ("alma.cycle4.4.cfg", "alma.cycle4.3.cfg", "alma.cycle4.2.cfg", and "alma.cycle4.1.cfg"). The parameters of these array configurations are described in detail in the ALMA Proposer's Guide of Cycles 4, 5, and 6.10 The tables of the antenna positions of these configurations are distributed with CASA.
6.1.3. Visibilities for TP Array
The TP array observes the sky as single-dish telescopes with a FWHM beam size of 56.7'' at 115 GHz. TP data are delivered as a calibrated image, or cube, with a cell size of 5.6''. Hence, we smooth the model images with a Gaussian with a FWHM of 56.7'' and regrid them on a 5.6'' cell size. We adopt the the same pointing coordinates as those of the 12 m and 7 m visibilities. Tp2vis is run on these images and generates 5,175 TP visibilities per pointing.
The model images do not have noise, and the visibility weights must be set arbitrarily. We apply the sensitivity-based weight (Section 4.1) with relative image rms sensitivities of 1 for each of the four 12 m configurations, 4.5 for the 7 m configuration, and 7 for the TP visibilities. These relative sensitivities are chosen based on typical ALMA mosaic data we have at hand (e.g., of nearby galaxies, Galactic molecular clouds), Table A-2 in the ALMA Proposer's Guide,11 and the ALMA sensitivity calculator. The visibility and sensitivity distributions of the TP, 7 m, and 12 m arrays are plotted in Figure 3.
Figure 3. Plot generated with Tp2vispl for the model data. The red, blue, and green correspond to the TP, 7 m, and 12 m visibilities for the mosaic field closest to the map center. (a): uv coverage. (b): amplitude as a function of uv distance. (c): weight density as a function of uv distance. (d): the same as (c), but for a smaller range of uv distance.
Download figure:
Standard image High-resolution image6.1.4. Caveats
Extra efforts are needed to circumvent some of the current problems in Clean/Tclean in Casa. In general interferometer observations, the uv coverages are different among mosaic pointings, and the PSF varies across the mosaic. The current version of Clean/Tclean (as of Casa 5.4) does not take this variation into account and uses a single PSF for all mosaic pointings in its minor clean cycles. This simplistic PSF deviates from the true PSF that reflects the uv coverage at each position. The deviation is larger for a larger mosaic, which often leads to an artificial flux divergence. To mitigate this problem, we explicitly set the uv coverage exactly the same for all the 38 pointings so that the PSF stays the same over the most part of the entire mosaic. This unique setup should not be a particular advantage for Tp2vis, since only the local PSF at the position of each emission affects clean results—the local PSF should be consistent with the local uv coverage at that position, but it does not matter whether the PSF is the same at other parts of the mosaic.
However, we note that even with the unique uv coverage for all pointings, the edge of a mosaic suffers from the PSF variation since it could be covered significantly by one array (e.g., the 7 m, TP arrays), but not by the others (e.g., the 12 m array), due to their different primary beam sizes. The PSF shape should be modified accordingly in such regions, as only a subset of the arrays contributes to the uv coverage.12 There is a tendency for current Clean/Tclean results to show a flux divergence when significant emission exists near the edge. The cause has not been entirely isolated, but the simplistic PSF likely plays a part, since Clean converges when each of the 12 m, 7 m, and TP data are imaged separately. Therefore, for our tests, we taper off the emission near the edge of the model images. For the Gaussian model we subtract a small constant flux from the whole image so that the flux decreases to zero at around the 80% level of the peak of the 12m+7m+TP combined primary beam. The flux outside is set to zero (Figure 2(a)). For the pseudo sky image we first make a combined primary beam pattern image, P, with Clean. We then multiply the original image by "(P2 − 0.5)", so that the flux becomes zero at around the ∼70%–80% level of the peak of the 12m+7m+TP combined primary beam. The flux outside is set to zero (Figure 2(b)).
The Tclean task also suffers from the same problem and appears to have another problem in calculation of the PSF. These issues in Tclean are far beyond the scope of this paper, but their effects and magnitudes should be characterized in the future. Here we adopt Clean as it currently appears somewhat more stable than Tclean for mosaic imaging.
6.2. Deconvolution and Results
We use the Clean task for deconvolution. The termination of Clean iterations is typically controlled by a threshold from the rms noise, or by the number of iterations. The model images do not have noise, and hence we use the number of iterations for termination and set it to 2 × 105. The gain is set to 0.05. The region for clean is restricted to the area above 80% of the peak of the 12m+7m+TP combined primary beam. We use the Briggs weighting with a "robust" parameter of +0.5. It results in a PSF of 1.59'' × 1.46'' with a position angle of 87.8° for both test images.
Figures 4 and 5 compare the model and cleaned images: (a) and (c) the original model maps smoothed with the PSF, (b) and (d) the cleaned maps with 12 m, 7 m, and TP visibilities, (e) the residual maps after the residual rescaling, and (f) the accuracy maps. Only relative fluxes are important for comparisons, so the fluxes of all images are normalized by a single constant so that the peak of panel (a) becomes equal to unity. Figures 4 and 5 are normalized separately. The accuracy maps show deviations from the input models and are calculated as
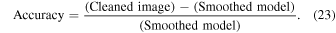
With this definition an accuracy map plus 1 makes a recovered flux ratio map at the 1.59'' × 1.46'' resolution. The clean is applied over nearly three orders of magnitude in flux as the residuals after clean are ≲0.3% of the peak flux (panel e). Over this wide dynamic range, the original flux is reproduced with errors mostly less than ∼5% (panel f), though some very diffuse regions show errors as high as ≳20%.
Figure 4. Results of joint deconvolution of TP, 7 m, and 12 m visibilities for the Gaussian image. The Clean task is used with niter = 200,000 and gain = 0.05. The PSF size is 1.59'' × 1.46'' with a position angle of 87.8°. (a) Model map smoothed with the PSF. (b) Cleaned map with 12 m, 7 m, and TP visibilities. (c), (d) The same as (a), (b), but on a log scale. (e) Residual map from clean. The operation of residual scaling has been applied. (f) Accuracy map. The deviation from the true flux is within ∼5% for the most part, and hence the quality of the cleaned map is very high. This map can be translated to the recovered flux ratio map by adding 1 across the image.
Download figure:
Standard image High-resolution imageFigure 5. Same as Figure 4, but for the pseudo sky image.
Download figure:
Standard image High-resolution imageThe purpose of this paper is to introduce the new Tp2vis package. Hence, these tests are performed with simple noise-free images. Further imaging simulations with more realistic setups would help evaluating systematic errors in actual ALMA observations.
7. Conclusions
We presented the Casa-based package "Total Power Map to Visibilities (Tp2vis)", which converts a TP map into visibilities. The TP visibilities, along with 12 m and 7 m visibilities, can be jointly deconvolved with standard deconvolvers (e.g., Clean). The Tp2vis package includes four functions: Tp2vis, Tp2viswt, Tp2vispl, and Tp2vistweak. The Tp2vis function generates a Gaussian visibility distribution, whose inversion, i.e., the synthesized beam, reproduces the primary beam of TP telescopes with natural weighting. The sensitivity-based weighing scheme is adopted as a default. The Tp2viswt function can manipulate the weights. The Tp2vispl function visualizes the TP weights with respect to those of 12 m and 7 m array data. After the joint deconvolution, the residual map should be re-scaled with the Tp2vistweak function. This rescaling is required due to the typical disparity between the areas of the synthesized beam and convolution beam.
The capability of Tp2vis was demonstrated using model maps. The joint deconvolution of 12 m, 7 m, and TP visibilities appeared very successful and reproduced the true emission distributions typically within 5% errors. The quality of images, of course, depends not only on the presence/absence of TP visibilities, but also on the distribution and contrast of the emission. Tests in wider parameter spaces with different deconvolvers are beyond the scope of this paper. Users are encouraged to do their own tests with model images that are similar to their objects of interest. We should note that our test was done under the idealized condition of no noise, but the 5% accuracy over the dynamic range of >∼2 orders of magnitude is quite encouraging. A manual of usage is presented in the Github repository (https://github.com/tp2vis/distribute).
We thank the anonymous referee for useful comments, the NRAO staff, in particular, Remy Indebetouw, Kumar Golap, Jennifer Donovan Meyer, Crystal Brogan, and John Carpenter for their help. We also thank Kazuki Tokuda, Fumi Egusa, Manuel Fernández, and Mercedes Vazzano for feedback on an early version of Tp2vis and Jim Barrett for comments on drafts. We acknowledge a research grant from the ALMA Cycle 4 Development Study program at NRAO. J.K. acknowledges supports from the National Astronomical Observatory of Japan and the Joint ALMA Observatory during his stay on sabbatical.
Appendix: GMC-like Model Map for Testing Interferometry Imaging
For tests of interferometer imaging procedures, we produce images of density/emission distributions similar to those in giant molecular clouds (GMCs). The method described below is similar to the one used for generating initial conditions for cosmological simulations of large-scale structures or galaxy formation, and to the one presented by Dubinski et al. (1995) for molecular cloud-like density fields. We generate a Gaussian random field that follows a density power spectrum (Section A.1) and manipulate it to enhance the contrast (Section A.2).
A.1. Model Density Field
We start from a representation of a density field with the density power spectrum  . We assume a Gaussian random field (i.e., Fourier modes are uncorrelated) and the probability distribution function of its amplitude is drawn from a Gaussian distribution.
. We assume a Gaussian random field (i.e., Fourier modes are uncorrelated) and the probability distribution function of its amplitude is drawn from a Gaussian distribution.
A.1.1. Definitions
Using the density at position  ,
,  , and average density, ρ0, the density contrast is defined as
, and average density, ρ0, the density contrast is defined as
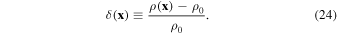
For the discrete Fourier transformation, we set the grid coordinates
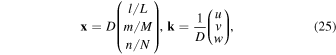
where (l, m, n) and (u, v, w) are integers, and (L, M, N) are the numbers of grid points in x, y, and z directions, and D is the size of the image, respectively. We adopt the definition of the discrete Fourier transformation:
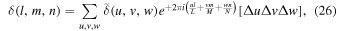
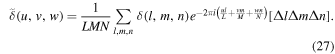
This definition is adopted in most numerical packages (e.g., IDL, Python Numpy package, etc) and is convenient for implementation. The last terms,  and ΔlΔmΔn (both=1), are written explicitly because they need an evaluation later. Since the density field, δ(l, m, n), is a field of real numbers, each complex Fourier component has to satisfy
and ΔlΔmΔn (both=1), are written explicitly because they need an evaluation later. Since the density field, δ(l, m, n), is a field of real numbers, each complex Fourier component has to satisfy
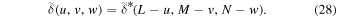
A.1.2. Power Spectrum and Normalization
The density power spectrum is often defined in the form of a power law P(k) = C k−n with a normalization constant of C. To avoid the singularity at k = 0 the power spectrum is redefined here as
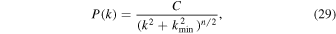
where kmin is the minimum wavenumber ( ).
).
The normalization constant C is calculated from the variance of the density contrast, σ2 (input parameter):
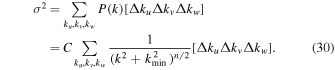
For the purpose of analytical evaluation, we can also obtain
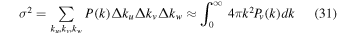
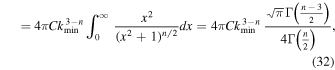
where the last equation is valid when n > 3 (the integral diverges when n ≤ 3). Γ is the gamma function. [Note  , and the size-line width relation of GMCs indicates n ∼ 4.] For a given set of n (>3) and σ, the normalization coefficient of the power spectrum is
, and the size-line width relation of GMCs indicates n ∼ 4.] For a given set of n (>3) and σ, the normalization coefficient of the power spectrum is
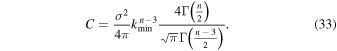
The above prescription generates a 3D data cube and involves a Fourier transformation in 3D. We can generate a 2D image and apply a Fourier transformation in 2D by using
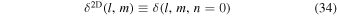
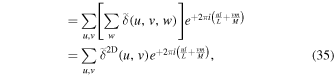
where
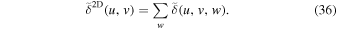
A.1.3. Realizations
The power spectrum P(k) and the fluctuation of density contrast  are related as follows.
are related as follows.
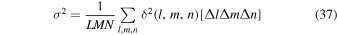
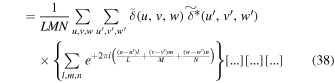
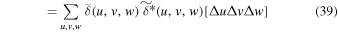
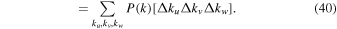
The {...} term is equal to  , where δK is the Kronecker delta. The bracket terms at the end,
, where δK is the Kronecker delta. The bracket terms at the end, ![$\left[{\rm{\Delta }}l{\rm{\Delta }}m{\rm{\Delta }}n\right]$](https://content.cld.iop.org/journals/1538-3873/131/999/054505/revision1/paspab047eieqn66.gif) ,
, ![$\left[{\rm{\Delta }}u{\rm{\Delta }}v{\rm{\Delta }}w\right]$](https://content.cld.iop.org/journals/1538-3873/131/999/054505/revision1/paspab047eieqn67.gif) , etc, are expressed as [...] to save space. From Equations (39) and (40),
, etc, are expressed as [...] to save space. From Equations (39) and (40),
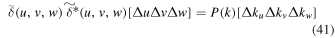
or
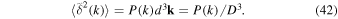
Note that ![$\left[{\rm{\Delta }}u{\rm{\Delta }}v{\rm{\Delta }}w\right]=1$](https://content.cld.iop.org/journals/1538-3873/131/999/054505/revision1/paspab047eieqn68.gif) and
and ![$\left[{\rm{\Delta }}{k}_{u}{\rm{\Delta }}{k}_{v}{\rm{\Delta }}{k}_{w}\right]=1/{D}^{3}$](https://content.cld.iop.org/journals/1538-3873/131/999/054505/revision1/paspab047eieqn69.gif) .
.
The Fourier components  are sampled using
are sampled using  as the variance. A random number is generated for each
as the variance. A random number is generated for each  using a Gaussian distribution with a standard deviation of
using a Gaussian distribution with a standard deviation of  . The phase of the complex number
. The phase of the complex number  is also drawn from a uniform distribution in [0, 2π), and the symmetry condition, Equation (28), is taken into account. Once all the Fourier components are generated, they are Fourier-transformed to the image plane using Equation (26). We could also draw the random numbers without the symmetry condition and take the real or imaginary part after the Fourier transformation. In this case, the amplitude should be multiplied by
is also drawn from a uniform distribution in [0, 2π), and the symmetry condition, Equation (28), is taken into account. Once all the Fourier components are generated, they are Fourier-transformed to the image plane using Equation (26). We could also draw the random numbers without the symmetry condition and take the real or imaginary part after the Fourier transformation. In this case, the amplitude should be multiplied by  .
.
Figures 6(a), (b) show the model images generated with a power spectrum index of n = 4, an average density fluctuation of σ = 0.3, and an image size of 16,3842. Both the real and imaginary images are shown. The images have periodic boundaries, and we spatially shifted them so that significant features come near the image centers.
Figure 6. Example model images with a power spectrum of index n = 4. One execution generates two realizations: (a) the real part and (b) the imaginary part, each of which has 16,3842 pixels. Panels (c) and (d) are generated from (a) and (b) by enhancing the bright parts as described in the text. Note that (a) and (b) are in a linear scale, while (c) and (d) are in a log scale.
Download figure:
Standard image High-resolution imageA.2. Enhance Density Contrasts
Figures 6(a), (b) qualitatively resemble some parts of GMCs. However, by construction, they don't have "dense cores", whose environs are often observed with ALMA. We could develop dense cores by running hydrodynamics simulations with gravity, starting from these images as the initial condition, but this is obviously beyond the scope of this paper. Here, to mimic their high brightness, we simply convert the flux  (or density
(or density  ) into new flux fnew using the following equation:
) into new flux fnew using the following equation:
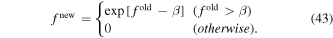
We adopt β = 0.7. This conversion is applied three times to make the images resemble GMCs with some dense cores. The final images are displayed in Figures 6(c), (d) in a log scale. They have larger dynamic ranges than the original ones, and thus are more challenging to reproduce with interferometer imaging.
Footnotes
- 7
- 8
Feather first deconvolves a TP map with BTP, and then multiplies
 in the Fourier domain. Therefore, it recovers the original TP map. In other words, Feather simply adds the original TP map.
in the Fourier domain. Therefore, it recovers the original TP map. In other words, Feather simply adds the original TP map. - 9
One should keep it in mind that the patterns of Ωsyn and Ωconv are still not the same, even though their areas are the same.
- 10
- 11
- 12








