Vacuum instabilities with a wrong-sign Higgs–gluon–gluon amplitude

New particles that obtain a portion of their mass from the Higgs boson also alter the Higgs potential. We will be primarily concerned with their effect on the Higgs quartic, which determines the mass of the Higgs boson once the appropriate vacuum is found. To compute the shift in the quartic, we use the one-loop Coleman–Weinberg potential determined from a mass matrix $\cal {M}$ for new bosons and fermions,

$$\begin{equation} V_{\rm CW} = \frac{1}{32\pi^2} \sum (-1)^F {\cal M}^4 \left(\log\frac{{\cal M}^2}{\mu^2} - \frac{3}{2} \right), \end{equation} \tag{ 1 }$$

expressing the mass of the new particles in terms of the Higgs field H, expanding as a function of H, and reading off the coefficient of |H|⁴ to obtain a correction δλ to the quartic. Note that when expanding around the origin and reading off the |H|⁴ term, we neglect possible |H|⁴ log|H|² terms that would arise from fields that are massless when the Higgs has no vacuum expectation value (VEV). Because we are interested in negative contributions to the hGG coupling, the dominant effect of increasing the Higgs VEV should be to decrease the mass of the fields we integrate out, and this is a reasonable approximation to use. (Note that in equation (1), μ, as is customary, denotes a renormalization scale.)

Corrections to the effective Higgs couplings to photons and gluons are easily understood in terms of the low-energy theorem [31, 32]. Namely, to read off the effective coupling induced by integrating out heavy particles, one treats them as a Higgs-dependent mass threshold in the beta function, obtaining the effective vertex from the running of 1/g², as a function of the Higgs-dependent mass matrix M²(h) for the new states:

$$\begin{equation} \fl -\frac{1}{4\,g^2} G^a_{\mu \nu} G^{a \mu\nu} \supset -\frac{1}{4} \left(-\frac{\Delta b}{16\pi^2} \log \det M^2(h) \right) G^a_{\mu\nu} G^{a\mu\nu} \supset \frac{\Delta b}{64\pi^2} \frac{h}{v} G^a_{\mu\nu}G^{a\mu\nu} \frac{\partial \log \det M^2}{\partial \log v}. \end{equation} \tag{ 2 }$$

with Δb the beta function coefficient of the states that were integrated out². An analogous statement holds for couplings to photons, the only difference being that it is the electromagnetic beta function coefficient that appears. In the case that the mass of the new particles is not much greater than half the Higgs mass, it can be important to take into account mass-dependent corrections to the low-energy theorem. In particular, for fermions these corrections are $1 + \frac {7 m_h^2}{120 m_F^2} + {\cal O}(m_h^4/m_F^4)$ and for scalars $1 + \frac {2 m_h^2}{15 m_S^2} + {\cal O}(m_h^4/m_S^4)$.

If we have a new colored state that carries charge Q and is in an SU(3)_c representation with quadratic Casimir C₂(R), we can evaluate its effect by rescaling the contribution of the top loop amplitude in the SM. Namely, defining

$$\begin{equation} R_g = \frac{\Gamma(h \to gg)}{\Gamma_{\rm SM}(h \to gg)}\quad {\rm and}\quad R_\gamma = \frac{\Gamma(h \to \gamma\gamma)}{\Gamma_{\rm SM}(h \to \gamma\gamma)}, \end{equation} \tag{ 3 }$$

we find that they are related by

$$\begin{equation} R_\gamma = \left[1 + 0.28 \xi \left(1 \mp \sqrt{R_g}\right)\right]^2, \end{equation} \tag{ 4 }$$

where the sign of the square root is determined by the sign of the hGG amplitude, and

$$\begin{equation} \xi = \frac{Q^2}{C_2(R)} \frac{C_2({\bf 3})}{Q_{\rm top}^2} = \frac{3 Q^2}{C_2(R)}. \end{equation} \tag{ 5 }$$

As discussed recently in, for instance, [34], the choices of charge and representation are fairly restricted by needing particles that can decay to the SM. This expectation is based on the lack of detected stable particles of exotic charge in searches of anomalously heavy isotopes of light elements [35, 36]; perhaps ambitious readers may consider exotic cosmologies that avoid such constraints, but we will proceed under the assumption that new exactly stable colored and charged particles do not exist. We plot the possible effects of several examples of plausible charge assignments in figure 2. Each of the curves has two branches meeting at R_g = 0, with the upper branch corresponding to the case with an inverted sign for the hGG amplitude. Notice that charge-2/3 color triplets can improve the fit, but other charges for color triplets are of little help in the inverted sign regime. (The charge 5/3 triplet discussed in [34] may help the fit slightly, but the best fit points have a negative sign of the new contribution to the hGG amplitude which is too small to completely cancel the SM amplitude, and hence the overall Higgs production rate decreased. This predicts that the measured rate for h → WW,ZZ should decrease in the future.) The combination of a neutral and charge 1 color octet with the same mass can give an interesting improvement in the fit. A color sextet of charge 2/3 can also offer some improvement. Other recent work in which new colored particles contribute to Higgs production and decay can be found in [37–40]. (As this paper was nearing completion, Dorsner et al [41] appeared advocating color octet or sextet scalars with opposite-sign hGG amplitude as a hint of unification. Given the vacuum stability and tuning arguments discussed below, we are much less sanguine.)

Zoom In Zoom Out Reset image size

Let us first consider the case of new fermionic states. We assume two vectorlike pairs of fermions, $\psi , \bar {\psi }$ and $\chi , \bar {\chi }$ with charges such that Yukawa couplings $H \bar {\psi } \chi$ and $H^{\dagger } \bar {\chi } \psi$ are allowed (e.g. ψ a doublet, χ a singlet with appropriate hypercharges), so that the mass matrix in the basis $\psi ,\chi ,\bar {\psi },\bar {\chi }$ is

$$\begin{equation} \cal{M}_{F} = \left(\begin{array}{@{}cc@{}} 0 & M_{F}^{\rm T}\\ M_{F} & 0 \end{array}\right), \end{equation} \tag{ 6 }$$

$$\begin{equation} {\rm where} \ \ M_F = \left(\begin{array}{@{}cc@{}} m_\psi & y_1 v \\ y_2 v & m_\chi \end{array}\right). \end{equation} \tag{ 7 }$$

In this case, the correction to the h → gg amplitude, relative to the SM amplitude from a top loop (and neglecting mass effects) is

$$\begin{equation} \frac{\delta A(hGG)}{A_{\rm SM}(hGG)} = 2 \frac{\Delta b_{\bf r}}{\Delta b_{\bf 3}} \left(1 - \frac{m_\chi m_\psi}{m_\chi m_\psi - y_1 y_2 v^2}\right). \end{equation} \tag{ 8 }$$

In particular, because there are vectorlike masses that are split by the mixing terms proportional to the Yukawas, we get a negative contribution to the amplitude. The factor $\frac {\Delta b_{\bf{r}}}{\Delta b_{\bf{3}}}$ is the ratio of the SU(3)_c beta-function coefficient of the representation that ψ and χ transform under, relative to the beta-function coefficient of a triplet.

Loops of fermions contribute a correction to the Higgs quartic, which in the special case m_ψ = m_χ = m is

$$\begin{equation} \delta \lambda_F = -\frac{N_{c;F}}{16\pi^2} \left\{\left(y_1^4 + y_2^4\right) \log \frac{m^2}{\mu^2} + \frac{1}{6}\left(5y_1^2 -2 y_1 y_2 + 5y_2^2\right)\left(y_1+y_2\right)^2 \right\}. \end{equation} \tag{ 9 }$$

As explained below equation (1), this was calculated by inserting the mass matrix of the fermions into the general formula and reading off the coefficient of |H|⁴ (i.e. expanding around the origin of the potential). The result in the more general case m_χ ≠ m_ψ is listed in the appendix. Notice that the logarithmic term here can be interpreted as encoding a beta function coefficient. Because the full renormalized potential must be independent of μ, the tree-level quartic must run in such a way as to cancel the μ-dependence of the Coleman–Weinberg potential. In other words, if we work in renormalized perturbation theory and impose renormalization conditions to relate our Lagrangian parameters to physical observables, all dependence on unphysical scales must cancel. The reader to whom this argument is unfamiliar may find the very clear discussion in chapter IV.3 of the textbook [42] enlightening.

Assume a mass matrix

$$\begin{equation} \cal{M}_S^2 = \left(\begin{array}{cc} m_1^2 + \lambda_1 v^2 & A v \\ A v & m_2^2 + \lambda_2 v^2 \end{array}\right). \end{equation}\noindent \tag{ 10 }$$

This arises, for instance, from a singlet scalar ϕ₁ and a doublet scalar ϕ₂ which each have mass terms, |H|²|ϕ_i|² quartic couplings with the Higgs, and a trilinear ϕ₁ϕ₂H coupling. It is the form that holds for squarks in the MSSM. The correction to the h → gg amplitude relative to the SM amplitude is

$$\begin{equation} \frac{\delta A(hGG)}{A_{\rm SM}(hGG)} = \frac{\Delta b_{\bf r}}{\Delta b_{\bf 3}} \frac{v^2 \left(\lambda_1 m_2^2 + \lambda_2 m_1^2 + 2 \lambda_1 \lambda_2 v^2 - A^2\right)}{4\left(\left(m_1^2 + \lambda_1 v^2\right)\left(m_2^2 + \lambda_2 v^2\right) - A^2 v^2\right)}, \end{equation}\noindent \tag{ 11 }$$

The factor of 1/4 arises from the relative beta function coefficients of a single color-triplet scalar and the top quark, whereas the factor $\frac {\Delta b_{\bf r}}{\Delta b_{\bf 3}}$ again corrects for the case when the field is not in the 3 of SU(3)_c. As in the case of fermions, the effect of mixing (here proportional to A) is to split the mass eigenstates and thus give a negative contribution. On the other hand, the quartic couplings λ_1,2 can give contributions of either sign.

The correction to the Higgs quartic in the case where the mass parameters m₁ and m₂ are equal is

$$\begin{equation} \delta \lambda_S = \frac{N_{c;S}}{32\pi^2} \left((\lambda_1^2 + \lambda_2^2)\log\frac{m^2}{\mu^2} + (\lambda_1 + \lambda_2) \frac{A^2}{m^2} - \frac{1}{6} \frac{A^4}{m^4}\right). \end{equation}\noindent \tag{ 12 }$$

The result in the more general case m₁ ≠ m₂ is given in the appendix. To compare to a more familiar expression: if the scalar states are stops in a supersymmetric theory, we have m²₁ = m²_Q3, m²₂ = m²_u^c3, N_c;S = 3, $\lambda _1 = y_t^2 + (\frac {1}{2}-\frac {2}{3}\sin ^2\theta _W) \cos (2\beta ) \frac {g^2 + g'^2}{2}$, $\lambda _2 = y_t^2 + \frac {2}{3}\sin ^2 \theta _W \cos (2\beta ) \frac {g^2 + g'^2}{2}$, and A = y_t(A_tsinβ − μcosβ). In particular, the part of δλ_S that is polynomial in A, dropping terms of order g², taking $m_{Q_3}^2 = m_{u^c_3}^2 = m_{\tilde t}^2$, and assuming large enough tanβ, is

$$\begin{equation} \delta \lambda_S \approx \frac{3}{16\pi^2} y_t^4 \left(\frac{X_t^2}{m_{\tilde t}^2} - \frac{1}{12} \frac{X_t^4}{m_{\tilde t}^4}\right), \end{equation}\noindent \tag{ 13 }$$

with X_t = A_t − μcot β. This is the familiar result that can be found in, for example, [43]. As for the logarithmic term, tops contribute $-\frac {3}{16\pi ^2}y_t^4 \log \frac {m_{\mathrm { t}}^2}{\mu ^2}$, so the μ-dependence cancels and the leftover logarithmic correction is $\frac {3}{16\pi ^2} y_t^4 \log \frac {m_{\tilde t}^2}{m_{\mathrm { t}}^2}$, which is also of the familiar expected form.

Given that we are looking for large changes to the Higgs potential that require light new colored and charged particles, it is reasonable to first consider whether stops can be responsible, since naturalness of electroweak symmetry breaking (EWSB) in supersymmetric theories favors light stops [29, 30]. In the case of stops, the general results discussed in the previous section imply a correction to the hGG amplitude (specializing the general result equation (11)):

$$\begin{equation} \frac{A(hGG)}{A_{\rm SM}(hGG)} = 1 + \frac{1}{4} \left( \frac{m_{t}^2}{m_{{\tilde{t}}_1}^2} + \frac{m_{t}^2}{m_{{\tilde{t}}_2}^2} - \frac{m_{t}^2 X_t^2}{m_{{\tilde{t}}_1}^2 m_{{\tilde{t}}_2}^2}\right), \end{equation} \tag{ 14 }$$

up to small D-term corrections (taken into account in the plots below). Here $m_{{\tilde {t}}_1}$ and $m_{{\tilde {t}}_2}$ are mass eigenvalues, not Lagrangian parameters. The effect of stops on Higgs branching ratios has been discussed in several papers in the recent literature [6, 17, 18, 24, 46], which reach a variety of conclusions. As emphasized by Blum et al [46], light unmixed stops tend to increase the hGG coupling and decrease the hγγ coupling, whereas highly mixed stops contribute large corrections to m²_Hu (thus requiring more tuning for EWSB) and lead to large corrections to b → sγ that must also be tuned away. The same considerations led [24] to focus on the 'funnel' region in which the stop corrections to hGG are small. On the other hand, the authors of [18, 22] argued for light and highly mixed stops in the region with the inverted sign of hGG, which could improve the fit to data.

We illustrate the parameter space that can achieve A(hGG) = −A_SM(hGG) in figure 3. As is clear from equation (14), this occurs at very large values of the mixing parameter X_t. This leads to a large splitting between the two stop mass eigenstates. In this region of parameter space, the lightest stop eigenvalue tends to be fairly light. For example, pushing the light eigenstate up to 450 GeV implies 20 TeV A-terms, which is an enormously finely-tuned scenario, both from the point of view of EWSB and of b → sγ. In fact, from the Coleman–Weinberg discussion in section 2.3, one can readily see that such large A-terms lead to very large negative threshold corrections to the Higgs mass. This implies the need for very large beyond-MSSM couplings of the Higgs boson that are capable of lifting its mass up to 125 GeV. When such couplings become large enough, it is difficult to imagine that other Higgs properties remain unmodified, so that considering only stop-loop modifications to the partial widths is dubious. On the other hand, one may wonder if the lower-left corner of the plot, with a light stop eigenstate, can fit the data, with large but no longer unreasonably large A-terms. It is still rather tuned. Recent experimental searches for direct production of light stops [47–52] constrain much of the stop parameter space with $m_{\tilde {t}_1} \stackrel {<}{{}_\sim } 500\,{\rm GeV}$, but only for sufficiently light neutralinos. The more squeezed regime will be probed by a combination of traditional missing-E_T signatures [53–62] and spin correlations [63], and even the case of R-parity violation may be constrained soon [64]. Nonetheless, for the moment, these considerations still allow as a logical possibility that light, highly mixed stops significantly alter the Higgs properties.

Zoom In Zoom Out Reset image size

However, vacuum instability poses an even more serious problem for this scenario than fine-tuning. The large A-term mixing is a trilinear scalar coupling $\tilde {t}_L \tilde {t}_R^{*} h$, so the potential can acquire large negative values when all three of these fields have VEVs. Because the Higgs and one stop eigenstate are relatively light, the barrier separating our EWSB vacuum from a color- and charge-breaking minimum can be relatively low. At large enough field values, quartic couplings arising from the Yukawa coupling will prevent the potential from being unbounded from below, even in the D-flat direction where the stop and Higgs VEVs are equal. Nonetheless, a deep charge- and color-breaking vacuum will exist when the A-term is large. This is illustrated with contour plots of the potential in figure 4. It remains to check whether the vacuum decay to this deep minimum happens fast enough to rule out this scenario.

Zoom In Zoom Out Reset image size

For this calculation we use the tree-level potential for the up-type Higgs H and the third generation squark superfields:

$$\begin{eqnarray} &&\fl V(H, {\tilde Q}_3, {\tilde u}^c_3) = m_H^2 \left|H\right|^2 + m_Q^2 \left|{\tilde Q}_3\right|^2 + m_U^2 \left|{\tilde u}^{c}_3\right|^2 + y_t^2 \left(\left|{\tilde Q}_3 {\tilde u}^c_3\right|^2 + \left|H {\tilde Q}_3\right|^2 + \left|H {\tilde u}^c_3\right|^2\right) \nonumber \\ &&+ \textstyle{\frac{1}{8}} g'^2 \left(\left|H\right|^2 + \textstyle{\frac{1}{3}} \left|{\tilde Q}_3\right|^2 - \textstyle{\frac{4}{3}} \left|{\tilde u}^c_3\right|^2\right)^2 + \textstyle{\frac{1}{8}} g^2 \left(\left|H\right|^2 - \left|{\tilde Q}_3\right|^2\right)^2+ \frac{4}{3} \left(\left|{\tilde Q}_3\right|^2 - \left|{\tilde u}^c_3\right|^2 \right)^2 \nonumber \\ &&+ \delta \lambda \left|H\right|^4 - y_t X_t H {\tilde Q}_3 {\tilde u}^c_3 - \left(y_t X_t H {\tilde Q}_3 {\tilde u}^c_3\right)^*. \end{eqnarray} \tag{ 15 }$$

We take $m_H^2 = -\frac {1}{2} m_h^2$ with m_h = 125 GeV the measured Higgs mass. Here δλ represents the corrections required to achieve the appropriate measured Higgs VEV; we remain agnostic about what model generates these corrections (in particular, we do not tie them to the stop masses and the MSSM radiative corrections). In the plot in figure 4, we have taken the fields to be real valued, with $H = \frac {1}{\sqrt {2}} h, \tilde {Q}_3 = \frac {1}{\sqrt {2}} \tilde {t}_L$, and $\tilde {u}^c_3 = \frac {1}{\sqrt {2}} \tilde {t}_R$. We ignore the down-type Higgs; at large tanβ, it should not be important, and more generally we do not expect that it will qualitatively alter the results.

Because the results of [45] are expressed as a scatter plot of points that are viable or not, it is not possible to do a systematic check from their results of whether the parameter space for which the hGG amplitude is inverted (as displayed in figure 3) is ruled out. Thus, we perform a new numerical calculation of the zero-temperature tunneling rate, using a slightly modified version of the CosmoTransitions software [65].³ The result is depicted in figure 5. In the right-hand panel, one can see that a bounce action S₀ ≳ 400, necessary for a sufficiently long-lived metastable vacuum to describe our universe, occurs only for a light stop mass eigenstate below 70 GeV. Such a light stop is excluded by LEP, even in the case of small $\tilde {t}_1-{\tilde \chi }^0_1$ mass splitting [66, 67].

Zoom In Zoom Out Reset image size

Here we will consider a different possibility that does not involve large mixing effects. If we drop the assumption of supersymmetry, we can consider charged scalar octets that have a mass that decreases with increasing Higgs mass,

$$\begin{equation} V = -\mu^2 H^\dagger H + \lambda_H \left(H^\dagger H\right)^2 + \left(m_O^2 - \lambda_{HO} H^\dagger H\right) O^\dagger O + \lambda_O \left(O^\dagger O\right)^2, \end{equation} \tag{ 16 }$$

with λ_HO > 0. This is a simplified subset of the interactions that arise, for example, for the Manohar–Wise scalar in the (8, 2)_1/2 representation of the SM gauge group [68]. Other interactions contract the SU(2) indices of H with those of O. There is no principled reason to ignore them, but we restrict to a low-dimensional parameter space for ease of plotting the results and because we expect it will capture the qualitative story of the interplay between vacuum stability and Higgs corrections. Quantitatively, it could be worthwhile to explore the full set of operators, but this is beyond the scope of this paper.

The Manohar–Wise representation contains both a neutral scalar O⁰ and a charged scalar O⁺; assuming they have the same mass, as they do with this simplified set of interactions with the Higgs, one finds that they affect the Higgs decay widths as shown by the dashed purple curve in figure 2, which comes rather close to the best-fit point of our simplified χ² fit. Effects of such an octet scalar on the hGG amplitude were considered recently in [69–71] in the regime with relatively small corrections that would lead to a reduced gg → H cross section. The possibility that λ_HO < 0 could lead to a reasonable fit of the data with enhanced diphoton rate was observed in [72]. Furthermore, as emphasized in [73], this regime of parameter space makes a striking prediction of a di-Higgs production rate hundreds or thousands of times larger than the rate in the SM.

In this case, the condition A_NP(hGG) = −2A_SM(hGG), at one loop and ignoring m²_O/m²_H effects, singles out a particular choice of λ_HO given the mass m²_O:

$$\begin{equation} \lambda_{HO} = \frac{16 m_O^2}{25 v^2}. \end{equation} \tag{ 17 }$$

Taking into account the (small) m²_H/m²_O corrections, we plot the required choice of λ_HO as a function of m²_O in figure 6 along with the physical mass of the octet. Notice that, unless the new octet state is very light, the coupling quickly becomes extremely large. In particular, once the physical octet mass reaches about 400 GeV, the coupling is nonperturbatively large. Hence, this scenario is only viable with relatively light states. In fact, the quartic part of the potential becomes unbounded below unless the condition

$$\begin{equation} \lambda_O \geqslant \lambda_{O;\min} \equiv \frac{\lambda_{HO}^2}{4 \lambda_H} \end{equation} \tag{ 18 }$$

is satisfied. We have also plotted $\lambda _{O;\min }$ in figure 6. It becomes nonperturbatively large already when m_O ≈ 300 GeV, a point at which the physical mass is only about 180 GeV. Of course, a potential that is unbounded below does not, strictly speaking, exclude the theory; this requires a check of the tunneling rate from our metastable vacuum to the runaway part of the potential, as in the previous section. We show this tunneling rate in figure 7, which indicates that a value of λ_O a factor of 1.5–2 below $\lambda _{O;\min }$ can yield an unbounded-from-below potential that is metastable enough to be compatible with the age of our universe.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

The full Lagrangian of [68], including further operators such as H^†aH^bO^†A_aO^A_b (with a,b SU(2)_L indices and A an SU(3)_c index) and Yukawa couplings of O to SM fermions, is beyond the scope of this paper. Nonetheless, we will make brief remarks on collider bounds. Minimal flavor violation Yukawa couplings of O to the quark fields lead to dominant decays $O^+ \to t{\bar b}$ and $O^0 \to t{\bar t}$ (when this mode is kinematically accessible). However, in most of the mass range that is viable for flipping the hGG amplitude, the decay to tops will be shut off. In that case, the searches for paired dijet resonances performed by ATLAS [74] and CMS [75] are likely the most sensitive probes of the scalar octets. (However, depending on the splitting within the SU(2)_L multiplet, searches relying on leptons may also set bounds [69].) The CMS dijet resonance study only constrains states above 320 GeV, due to the relatively hard cuts required by high-luminosity running. The ATLAS study relied on early data with lower trigger thresholds, and bounds sgluons to be heavier than 185 GeV. Because we have multiple octet states, it is possible that the bound is stronger, but this conclusion depends on details of the branching ratios of our octets. Rather than undertake a full study of the collider bounds, we show the 185 GeV bound in figures 6 and 7 as a rough guideline. This shows that the viable parameter space is in a narrow range of masses above the bound and at strong coupling λ_O ≳ 4, unless the octet decays in a way that evades the ATLAS search. A more detailed discussion of constraints on Manohar–Wise octet scalars may be found in [76]. Another recent update on collider bounds is in [77].

Having explored the effects of scalars that change the sign of hGG with large mixing effects or with negative quartics, and shown that there are vacuum stability problems in both cases, we should make some remarks on the case of fermions. Because qualitatively similar observations were made recently in [44], we will be brief. The essential point is that new color triplet fermions with Yukawa couplings to the Higgs contribute terms $\frac {\mathrm {d}\lambda }{\mathrm {d}t} = -\frac {3}{8\pi ^2} y^4$ in the renormalization group equation (RGE) for the Higgs quartic. These corrections drive λ negative at relatively low energies, leading to yet another vacuum instability. Of course, there is a way out: if the new colored fields come in complete supermultiplets, the scalars contribute an opposite contribution to the running of λ and the quartic can be saved from turning negative. Thus, one perspective on this correction is that it gives a bound on the size of the allowed splitting between fermions and scalars in the new multiplet; this is essentially the naturalness point of view discussed in [44].

The first observation relates to fermionic top partners. In particular, suppose we have new fields $T, \overline {T}$ in the (3,1)_±2/3 representations of the SM gauge group. We can add both a vectorlike mass for these fields and a mixing term with the SM left-handed quarks,

$$\begin{equation} M T {\overline T} + y_T H Q {\overline T} + y_{\overline T} H^\dagger {\overline Q} T. \end{equation}\noindent \tag{ 19 }$$

Such top partners contribute a correction to the hGG amplitude:

$$\begin{equation} \frac{A(hGG)}{A_{\rm SM}(hGG)} = 1 - \frac{v y_T y_{\overline T}}{M y_t - v y_T y_{\overline T}}. \end{equation}\noindent \tag{ 20 }$$

If we wish this to equal −1, we must take $y_T y_{\overline {T}} = \frac {2}{3}y_t \frac {M}{v}$. If the new colored states are to be heavier than the top quark, this requires large Yukawas. Furthermore, these states are highly mixed with the top, and require that we significantly alter y_t from its SM value. This is an awkward solution that will be difficult to reconcile with experimental bounds.

A safer approach is to add a pair of vectorlike fermions, as in section 2.2, which are not mixed with the SM top. To be concrete, we will take these states to have the same quantum numbers as the SM Q and u^c fields, but with a parity that prevents mixing terms with the SM. Furthermore, we will simplify the story by taking m_χ = m_ψ = M and y₁ = y₂ = y. Obtaining the amplitude A(hGG) = −A_SM(hGG) then requires that $y^2 v^2 = \frac {1}{2} M^2$, with mass eigenvalues about M_light ≈ 0.29M and M_heavy ≈ 1.7 M. The finite correction to λ (which must have a value of about 0.13 for the correct Higgs VEV) from the Coleman–Weinberg formula can then be expressed as $-\frac {M^4}{4\pi ^2 v^4} \approx -3.4 \frac {M_{\rm light}^4}{v^4}$, so that as we raise the mass scale of the new colored fermions relative to the top mass, the tuning in the Higgs sector increases quartically.

Finally, we give an approximate solution of the RGEs to see at what scale Λ the Higgs quartic drives the potential unstable, when $\lambda (\Lambda ) = \frac {2\pi ^2}{3\log (H_0/\Lambda )}$ (with H₀ the Hubble constant), as in [44]. The Hubble scale appears in this estimate because we are asking if the bounce is rapid relative to the age of the universe, and the other numerical factors arise from a simple approximation that the bounce action is ≈8π²/(3|λ|), as explained in [78]. For simplicity we have dropped terms in the RGEs proportional to g₁, which do not significantly change the results. We begin at the $\overline {MS}$ top mass in the SM, run up to the scale M using SM beta functions, and then run to higher energies with the new physics beta functions, turning on y₁ = y₂ at M. In this case, denoting the common value of y₁ and y₂ simply as y, the beta functions are altered as:

$$\begin{eqnarray} 16\pi^2 \beta(y_t) & = & 16\pi^2 \beta(y_t)_{\rm SM} + 6 y_t y^2, \nonumber \\ 16\pi^2 \beta(\lambda) & = & 16\pi^2 \beta(\lambda)_{\rm SM} + 24 \lambda y^2 - 12 y^4, \nonumber \\ 16\pi^2 \beta(y) &=& y\left(\frac{15}{2} y^2 + 3 y_t^2 - 8 g_3^2\right), \nonumber\\ 16\pi^2 \beta(g_3) &=& 16\pi^2 \beta(g_3)_{\rm SM} + \frac{4}{3} g_3^3. \end{eqnarray}\noindent \tag{ 21 }$$

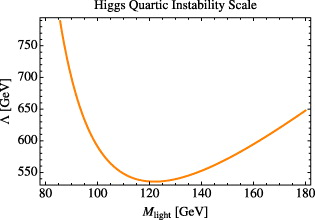
The result of integrating the RGEs is shown in figure 8. The rising curve at M_light ≳ 120 GeV approximately tracks the value of M ≈ 3M_light, indicating that λ runs negative essentially immediately when we turn on the RG effects of the new states. A better calculation would correctly take into account the running between the thresholds M_light and M_heavy, but this plot makes our qualitative point: if new fermionic states are to change the sign of the hGG amplitude, not only do they imply an uncomfortably large amount of fine-tuning and strong coupling, but their superpartners must be nearby. Otherwise, they are ruled out by a catastrophic vacuum instability, much like the scalar cases we have studied.

Zoom In Zoom Out Reset image size