Resolved Stellar Population of Distant Galaxies in the ELT Era

One of the key issues in modern astronomy concerns star formation history (SFH) in the universe. Direct observations of galaxies up to high redshift can be used to map the SFH, but since the integrated galaxy light is dominated by the contribution of the most recent generations of stars, the information that can be derived on the underlying older stellar population is severely limited. However, the SFH in galaxies can be uncovered by interpreting the color-magnitude diagrams (CMDs) of their stars, which contain the fossil record of their SFH (e.g., Greggio et al. 1993; Holtzman et al. 1999; Brown et al. 2006; Cole et al. 2007; McQuinn et al. 2009; Weisz et al. 2011; see also Cignoni & Tosi [2010] for a review). This kind of study requires accurate photometry down to faint magnitudes in crowded fields, which with current instrumentation is feasible only for the nearest galaxies. This implies a very limited sampling of the SFH in the universe, with plenty of dwarfs, a few spirals, and no giant elliptical galaxies.

By the end of this decade this situation is expected to change significantly, as a number of extremely large telescopes, such as the Giant Magellan Telescope (GMT; Johns 2008), the Thirty Meter Telescope (TMT; Szeto et al. 2008), and the European Extremely Large Telescope (E-ELT; Gilmozzi & Spyromilio 2007), come into operation. The large collecting area of ELTs coupled with adaptive optics cameras able to deliver quasi-diffraction-limited images will allow us to probe a wide volume, where we can access a significative sample of galaxies. More importantly, it will be possible to study dense stellar fields. Indeed, because of crowding, stellar photometry in external galaxies is currently feasible only in regions of relatively low surface brightness. For giant galaxies, this prevents us from deriving a detailed SFH where most of the galaxy mass is located. One of the key advantages of taking images with extremely large aperture telescopes is the exceptionally good image quality when the telescope can work close to its diffraction limit. This significant improvement has two fundamental effects: (1) it produces a dramatic reduction of the background light over the point-spread function (PSF) area considered for the photometry; (2) it allows a significant improvement in the spatial resolution (proportional to the telescope aperture). These combined advantages offer the unique opportunity to carry out observations of faint targets in crowded and/or structured objects (galaxies) at large distances, which cannot be exploited by any other telescope of smaller aperture, either ground-or space-based. In summary, the excellent resolution capabilities of next-generation large-aperture telescopes will enable us to study high surface brightness regions, i.e., the inner parts of galaxies, where star formation is more conspicuous, as well as to directly address age and metallicity gradients.

The photometric performance of ELTs operating close to the diffraction limit was investigated by Olsen et al. (2003) and by Deep et al. (2011). Both studies focus on the impact of crowding conditions on the photometric quality, as quantified by the 1σ width of the error distribution as a function of magnitude, for stellar fields with different surface brightnesses. In this approach, errors are considered to be symmetric, with stellar luminosities having the same probability of being overestimated or underestimated. However, crowding induces asymmetrical photometric errors, with an excess of stars measured brighter than they really are (e.g., Tosi et al. 1991; Gallart et al. 1996; Renzini 1998). This results in artificially brightened features on the CMD, which may induce a systematic error in those parameters (e.g., distances and stellar ages) that are derived from their luminosity. In addition, crowding may also affect systematically the distribution of stars across the CMD, jeopardizing its interpretation in terms of star formation history. The impact of this asymmetry is negligible under low-crowding conditions (e.g., when the 1σ width is smaller than about 0.1 mag), but grows rapidly with crowding. In this article, we present the results of end-to-end simulations of two specific science cases aimed at investigating the SFH in galaxies, which fully exploit the unprecedented capabilities foreseen for ELTs.

There are several interesting programs concerning the study of resolved stellar populations in external galaxies, like the analysis of multiple generations in globular clusters (see Piotto 2009 and references therein); the determination of the initial mass function and its variations (e.g., Kroupa 2001); the recovery of the spatially resolved SFH in isolated and in interacting galaxies (e.g., Cioni et al. 2011 for the Magellanic system); and tracing the galaxy assembly process through the counts of resolved stars and detection of streams (e.g., Ferguson 2007). Here we focus on the possibility of deriving global information on the star formation history for a significative sample of galaxies with a modest time investment. This means targeting distant galaxies, so that the field of view samples a fair fraction of their mass, and observing galaxies in groups or clusters, so as to enable the study of a representative galaxy population. On these premises we have concentrated on the following science cases: (1) deriving basic information on the SFH in the central region of a disk galaxy at the distance of the Centaurus Group and (2) studying the metallicity distribution at half of the effective radius of an elliptical galaxy in the Virgo Cluster. For these cases, we have developed simulations of stellar photometry, based on synthetic stellar populations and assuming the expected performances of the adaptive optics assisted near-IR camera (MICADO; Davies & Genzel 2010) for the E-ELT (see details in § 3.1). The resulting CMDs were analyzed to assess the impact of the photometric errors on the specific science goal.

In § 2 we describe our selected science cases. In § 3 we report details of our simulation and the following photometric analysis. Results of this study are given in § 4 with general conclusions summarized in § 5.

The derivation of the SFH in galaxies from the CMD of their resolved stars is routinely performed with the synthetic CMD method (Tosi et al. 1991; Tolstoy &; Saha 1996; Aparicio et al. 1996; Harris & Zaritsky 2001; Dolphin 2002), which aims at minimizing the distance between the observed stellar density distribution across the CMD and corresponding models by varying the strength of the successive star formation episodes. The method basically rests upon age-dating and counting stars in diagnostic regions on the CMD (see, e.g., Greggio 2002; Greggio & Renzini 2011), and the derived SFH depends on the age sensitivity of characteristic features sampled in the observed CMD (Gallart et al. 2005). Stellar age dating is most accurate for stars at the main-sequence (MS) turnoff (TO); at the other extreme, the red giant branch (RGB) collects stars born over (almost) the total range of ages present in the galaxy. Also, the horizontal branch (HB) is populated by stars in a very wide range of ages, but the truly old populations can be distinguished as RR Lyrae stars or blue HB stars.

Figure 1 shows the limiting magnitudes for isolated point sources that are expected for MICADO at E-ELT with 5 hr of total integration, together with the typical magnitudes of RGB tip stars, red HB stars, and MS TO stars with an age of 10 Gyr, at a distance modulus of DM = 28.3. Comparing the observational limits with these characteristic magnitudes, we derive the typical distances up to which these features can be detected and measured with a relatively good S/N (i.e., ∼10, see Table 1). It appears that we could sample old MS TOs only within the Local Group and little beyond, while for galaxies in the Centaurus Group (DM = 28.3) we will measure HB stars with high S/N. In the nearest galaxy cluster (Virgo, DM = 31.3), the portion of CMD accessible with a reasonable exposure time is limited to the (upper) RGB and brighter magnitudes. Actually, the Hubble Space Telescope already provides us CMDs down to these limits but only in sparsely populated regions; for example, in Centaurus A, HB stars were detected (Rejkuba et al. 2005) with ∼9 hr exposures, in a region located at ∼40 Kpc from the center (μ_K ∼ 26). At this distance, the portion of the CMD at magnitudes brighter than M_I ∼ -2 has been measured and analyzed for late-type dwarfs around M83 (Crnojević et al. 2011). Similarly, photometry down to ≃1 mag below the tip of the RGB was obtained by Caldwell (2006) for dwarf galaxies in Virgo. The real gain we expect with MICADO concerns the ability of deriving data of similar quality in high surface brightness regions within galaxies, to the advantage of sampling the bulk of the star formation in medium size and giant galaxies. The simulations described in this article aim at checking this quantitatively for the two specific science cases described below.

Zoom In Zoom Out Reset image size

2.1. The SFH in a Disk Galaxy in the Centaurus Group

Figure 2 shows a synthetic CMD, which can be considered as representative of the stellar population in the disk of a late-type galaxy, with the synthetic stars color-coded according to their age, as labeled. We examine here the possibility of recovering basic information on the SFH for such a stellar population placed at a distance of ≃4.5 Mpc. Four diagnostic boxes (see Table 1) are superimposed on the synthetic CMD, with the aim of targeting specific age ranges, i.e., the red supergiant (RSG) box for the youngest component; the blue supergiants (BSG) and asymptotic giant branch (AGB) boxes for the intermediate-age components; the RGB box for the old component. The age distributions of the stars falling in each of the four boxes is plotted in Figure 3, showing that there is little age overlap in the various boxes. The simulation allows us to estimate the average number of stars per unit stellar mass formed in the age range sampled by each box, hereafter referred to as specific productions (P_box), reported in Table 2. Star counts in these diagnostic boxes performed on an observational CMD allow us to recover quantitative information of the SFH in the observed field over the whole galaxy lifetime: it suffices to divide the star counts by the appropriate specific productions to derive the average mass turned into stars in the corresponding age range. This method is not as sophisticated as the full synthetic CMD method, which fits the detailed stellar distribution using small boxes, but it is much more straightforward and easily applicable to large datasets. At any rate, the reliability of the derived SFH depends on the completeness of the counts within the boxes, sensitive to the photometric error which moves the stars from or into adjacent regions of the CMD. Therefore, we expect a dependence of the result on the crowding conditions, i.e., on the surface brightness of the sampled galaxy region. In the following we test how the star counts in these boxes are affected for a stellar field in the very center of a disk galaxy located in the Centaurus Group, adopting a distance modulus of m - M = 28.3 and no extinction.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

2.2. The Metallicity Distribution for Stars in a Giant Elliptical in Virgo

Figure 4 shows the luminous portion of the CMD of an old stellar population with a wide metallicity distribution, akin to elliptical galaxies. Of the four diagnostic boxes drawn in Figure 2 only the RGB box is populated, and includes 3232 stars, yielding a specific production of for this stellar population. The absence of stars in the RSG, BSG and AGB boxes implies (virtually) no star formation at ages younger than ≃1.5 Gyr, whereas by dividing the star counts in the RGB box by P_RGB one obtains the mass transformed into stars in the field. More interestingly, the color distribution of the bright RGB stars can be used to recover their metallicity distribution, as in, e.g., Harris & Harris (2002). The different metallicity bins separate much better on the central panel of Figure 4, due to the higher temperature sensitivity of the wider color baseline. In this respect, an optical-infrared color provides the best leverage for the determination of the metallicity distribution of the RGB stars. The horizontal bars in the left and central panels of Figure 4 show the size of a 0.1 mag error on the respective color: clearly the photometric accuracy needed to recover the metallicity distribution is less demanding in the optical-infrared CMD than in the infrared CMD. At any rate, photometric errors smear out the true color distribution of the stars, thereby affecting the derivation of the underlying metallicity distribution. Thus, the accuracy of this distribution determined from the analysis of the CMD is sensitive to crowding conditions. In the following we test the effect of the photometric errors for a stellar population located at half the effective radius of an elliptical galaxy in the Virgo Cluster, adopting a distance modulus of m - M = 31.3 and no extinction.

Zoom In Zoom Out Reset image size

Simulated images were constructed with a tool¹ developed during the Phase A study of MICADO (Falomo et al. 2011). The simulator is able to generate synthetic frames with a large variety of telescope and instrument parameters, as well as for input field of stars and/or galaxies. In the MICADO at E-ELT configuration, all the relevant parameters of the telescope and of the instrument are included, as well as the conditions of the observations. For the simulated images presented here, we assumed a 1277 m² collecting area, a total throughput of 0.4 and 0.39, respectively, in the I and K bands, a read noise of 5 e, and a plate scale of 3 mas pixel^-1. We assumed the typical near-IR sky background at Paranal (Chile) and included the contribution of thermal emission in the near-IR-bands; specifically we adopted a background of 20.1, 16.3, and 12.8 mags in the I, J, and K bands, respectively.

3.1. MICADO

MICADO is the Multi-AO Imaging Camera for Deep Observations, designed to work with adaptive optics (AO) on the 42 m E-ELT (Davies et al. 2010). MICADO is optimized for imaging at the diffraction limit and will fully sample the 6–10 mas full width at half-maximum (FWHM) in the J - K bands. With a throughput exceeding 60%, its sensitivity at 1–2 μm will be comparable with that of James Webb Space Telescope (JWST) for isolated point sources, but MICADO's exquisite resolution will allow us to investigate regions with a much higher crowding compared with JWST. The instrument is able to image a relatively wide (53^'' × 53^'') field of view, and a large number of wide- and narrowband filters is foreseen, ranging from the I to the K band.

The simulations assume that the images are obtained using MICADO in conjunction with MAORY, the post-focal adaptive optics modules currently under study for the European Extremely Large Telescope. The MAORY (Diolaiti et al. 2010 Foppiani et al. 2010) module uses six laser guide stars to produce multiconjugate AO (MCAO) correction. We assumed the PSF computed with a seeing of 0.6^'',² with FWHM of 4 mas, 5 mas, and 9 mas in the I, J, and K bands, respectively. Since the field of view of our simulation is small compared with the expected PSF variation on the total field of MICADO, we assumed a fixed PSF over the whole simulated frame. Specifically, we used the MAORY central PSF mapped over 2048 × 2048 pixels. In Figure 5 we show a representative image of the adopted PSF in the J band. The PSF in the I and K bands have a very similar shape but different Strehl (i.e., the ratio of peak diffraction intensities of an aberrated vs. perfect wavefront) and encircled energy values. Figure 6 shows the radial growth of the encircled energy in the photometric bands used for our simulations. These distributions present a very sharp central peak, which becomes progressively more pronounced going from the I to the K band, reflecting the trend of the Strehl ratio. A quantitative characterization of the PSF is included in Figure 6.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

3.2. Input stellar populations

Table 3 lists the properties of the input stellar populations of the two science cases: (1) the central region of a disk galaxy in the Centaurus Group (hereafter young stellar population) and (2) a region located at half of the effective radius of an Elliptical in the Virgo cluster (hereafter old stellar population). Illustration of CMDs for the two stellar populations are shown in Figures 2 and 4, where we also specify the adopted star formation histories.

The input stellar lists are generated from theoretical simulations following a procedure described in detail in the appendix; here we only mention that special care was devoted to ensure (1) adequate sampling of the short lived evolutionary stages, and (2) completeness of the input stellar list in all the photometric bands used in the specific science case. The size of the simulated population follows from the proportionality between the number of stars brighter than a given magnitude limit and the total luminosity of the stellar population sampled by the synthetic frame:

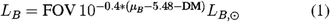
where FOV is the field of view in square arcseconds, μ_B is the (unreddened) surface brightness of the stellar population, DM is the distance modulus, and we have adopted a solar absolute magnitude in the B band of M_B,⊙ = 5.48.

In order to keep the input stellar list within a manageable size, only objects brighter than a threshold magnitude are considered as point sources, while the remaining light of the stellar population is distributed over the frame as a pedestal, with its associated Poisson noise. The threshold magnitude is chosen ∼1.5 mag fainter than the limiting magnitude (S/N = 5) of the telescope + instrument combination for the assumed exposure time. This ensures that the effect of blending of stellar images is well described also at the faint end of the luminosity function.

3.3. Synthetic Frames

The AETC tool with the MICADO configuration was used to generate images in the I, J and K bands for the two science cases in Table 3. Note that the mass-to-light ratio and the colors are univocally determined by the adopted SFH, while the stellar mass (M_SF), sampled by the frame, depends on the chosen surface brightness, distance and field of view. For the young case, the input stellar list consists of 644,483 stars brighter than K = 30.7 ; for the old case, it counts 125,058 stars brighter than K = 31. The input lists specify mass, age, metallicity, magnitudes in the I, J, and K bands, and coordinates on the frame for each star. Synthetic frames are generated from them in the corresponding bands and Figures 7 and 8 show sections of the J -band simulated images. The wide magnitude range of the objects in Figure 7 is readily visible, with a few very bright stars showing the characteristic pattern of the PSF. Note that many objects are detected under the halo of the bright stars due to the narrow core of the PSF. The image in Figure 8 has a very different appearance, with many stars of comparable brightness: this reflects the different properties of the luminosity function of the two populations.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

3.4. Photometric Analysis and Methodology

4.1. Photometric Quality

Having full knowledge of the input star list, we can evaluate the quality of the photometry object by object. In order to pair detections to input sources, it is necessary to define a matching algorithm, a task which is not completely trivial. We use a search radius of 1 pixel to select candidate mates of each detected source; within such area we may find (1) no input source, (2) one input source, (3) more than one input source. Case 1 corresponds to spurious detections, due to, e.g., noise spikes, or interference of the wings of the PSF of neighboring bright stars; case 2 corresponds to a one-to-one match, while in case 3 we have the embarrassment of more than one possible (input star) mate. We adopt the criterion of choosing as counterpart the brightest among the candidates. Different criteria could be envisaged (e.g., imposing a limit on the difference between the input and output magnitudes), all however getting into trouble at faint magnitudes, when approaching the confusion limit. Our choice has the merit of being totally independent of the magnitude difference between the input and output source, which is in fact the subject of the analysis described in the following.

4.1.1. The Young Stellar Population at 4.6 Mpc

The simulated images for this science case include ∼650,000 stars with J, K ≤ 31 ; the photometric measurement yields ∼163,000 sources detected in J and K bands of which ∼159,000 have a matched counterpart in the input list, while ∼4000 (i.e., ∼2% of the detections) are spurious objects. Most of these fake sources are located around input bright stars and are features of the PSF (see Fig. 5) misinterpreted as stars by the reduction package because of a nonperfect subtraction of the PSF. Figure 9 compares the luminosity function of the output catalogue (thick lines) to that of the input data (thin line). The luminosity function appears very well recovered brighter than J ∼ 26.5, K ∼ 25.5, while a strong incompleteness is evident fainter than J, K ∼ 29. In the intermediate magnitude range, the output luminosity function counts an excess of stars compared with the input data because of blending, i.e., a luminosity increase of the detected source due to overlapping PSFs, as argued below. In Figure 9 we also show the luminosity function of the input stars which have been position-matched (shaded histogram): clearly only a fraction of the input stars are recovered in each bin, which is the true completeness, or the probability of detecting a star of given input magnitude. Due to photometric errors, the position-matched stars can be found in different bins, typically brighter than their true value, which is the reason why the output luminosity function exceeds the input one at most magnitudes except for the brightest bins, where photometry is very accurate. At the faintest magnitudes, incompleteness is boosted by the low S/N and stellar background, and the output luminosity function drops to zero.

Zoom In Zoom Out Reset image size

The photometric quality is further illustrated in Figure 10, where we compare the magnitudes of the matched objects. The brightest stars are clearly recovered with a small error, but as the input magnitude increases, the distribution of the discrepancies widens as the stars are measured as either fainter or brighter than they are. Close to the faint end of the input magnitude distribution, the source detection is favored if the local background is low, and/or the star is blended with other sources. Therefore, at the faintest input magnitudes, positive errors (i.e., output magnitude ≳ input magnitude) become undersampled, and belowsome threshold stars are recovered only if measured brighter than they are. The slanted limit in the right panel of Figure 10 corresponds to the detection threshold used in the reduction of the K -band image, i.e., an output magnitude of ≃29. The effect of blending is present over a wide magnitude range, and leads to an asymmetrical distribution of the photometric errors, which extends over a wider range on the negative side compared with the positive side. Note, for example, that the clump stars (at J ≃ 27.3) can be recovered up to 1 mag brighter, or up to 0.5 mag fainter than they are. Although the average error at this magnitude level is very close to zero, and the peak of the luminosity function due to clump stars well recovered by the photometry (see Fig. 9), the spurious excess of stars above the true clump can be misinterpreted when analyzing the CMD, e.g., as due to a younger stellar generation. Figure 10 also shows that negative errors are much more frequent for sources for which multiple candidate counterparts were found in the input stellar list, again demonstrating the constructive interference of stellar crowding, which leads to an artificial brightening of the detected sources.

Zoom In Zoom Out Reset image size

The asymmetry of the photometric errors is traced by the median of their distribution (which becomes progressively more negative as the input magnitude gets fainter), as well as by the 1σ widths of the error distributions, computed independently for the stars measured brighter (lower locus in Figs. 10 and 11) and those measured fainter (upper locus) than they truly are. The asymmetry of the 1σ width appears much more pronounced in the J rather than in the K band because of the higher background in the latter filter. Actually, the total error mainly results from the shot noise of the sky and thermal background plus the error associated with the underlying stellar population. In the K band, the first contribution (which induces a symmetrical error) largely dominates over the second. The opposite holds in the J band, where the effect of the underlying stellar population can be better appreciated as an asymmetrical error distribution due to blending.

Zoom In Zoom Out Reset image size

4.1.2. The Old Stellar Population at 18 Mpc

The simulated images for this science case include ∼125,000 stars with K ≤ 31 and J, I magnitudes down to 31.7 and 32.5, respectively. The photometric measurement yields ∼22,350 sources detected in I, J and K, of which ∼21,700 have a matched counterpart in the input list, while ∼650 (i.e., ∼3% of the detections) are spurious objects. Also in this case, most of the spurious detections come from a nonperfect PSF subtraction, and also in this case the spurious sources are a small fraction of the total number of objects, so that the overall appearance of the CMD and of the LF is not significantly affected.

As for the young stellar population, Figures 11 and 12 illustrate the photometric quality for the old stellar population. This science case differs from the previous one in the distance modulus (3 mag fainter) and in the magnitude range covered by the input star list, because of the absence of the young- and intermediate-age components. The input luminosity function (thin lines in Fig. 12) does include the HB, at 31 ≲ I ≲ 32, 29.5 ≲ K ≲ 30.5, but only very few of its stars are position matched (see shaded histogram), and in most cases they are assigned a too bright magnitude. The migration of stars towards brighter bins along the luminosity function due to blending is evident also in this case, and can be appreciated as the difference between the shaded region and the output luminosity function (thick line histogram). It is interesting to note that the cut off of the I -band output luminosity function is more smooth than that of the K -band one. This is due to the measurement procedure adopted which, once a source is detected on the K image, forces the detection at the shorter wavelengths, so that the adopted detection threshold translates into a sharp cut off only in the K -band luminosity function.

Zoom In Zoom Out Reset image size

The distribution of the photometric errors (Fig. 11) presents similar characteristics to those described for the young stellar population case: due to blending, the median error is negative almost all along the magnitude range covered, and the error distributions are skewed towards the negative side. Compared with the young one, the old population science case is characterized by a much higher crowding, in spite of the similar surface brightness, because of the ∼4 times larger distance. For this reason, the error distributions are wider for the old than for the young case, particularly on the negative side (see Figs. 10 and 11, right panels).

The I band appears to be heavily affected by crowding (see Fig. 11, left panel): in spite of the low sky background in the optical, the 1σ loci show that the total error distributions are very wide, and skewed on the negative side, again showing the effect of stellar blending. We note that the brightest sources are affected by a large error, which exceeds what is expected from the shot noise. We attribute this effect to a nonoptimal sampling of the PSF in the I band, which has a nominal FWHM of less than 2 pixels, rather than to the underlying stellar population. Although DAOPHOT is able to reconstruct such peaked PSF, the measurement of the magnitude is complicated by uncertainties in the position of the centroid. The use of ALLFRAME, i.e., taking advantage of the information on the J -and K -band images, greatly improves the quality of the I -band photometry; nevertheless, an error associated to the undersampling is present all over the magnitude range, and particularly visible at the bright end.

A science case similar to the one discussed here is presented in Deep et al. (2011), albeit with some differences, including the CMD of the synthetic stellar population, and the exposure time, for which Deep et al. (2011) adopt 1 hr. In addition, in Deep et al. (2011), the simulated PSF has a coarser sampling than ours, and the instrument background is neglected. In spite of these differences, for the same surface brightness, our results are broadly compatible with theirs in the I and J bands, with similar 1σ values at the bright end.

To summarize: the comparison of the input and output catalogues shows that, roughly for both science cases, the output luminosity functions become 50 % incomplete at J, K ∼ 29, I ∼ 30.5, while a photometric error of σ ≃ 0.2 mag is reached at J ∼ 29.5, K ≃ 28 and I ∼ 30, similar to the S/N = 5 limits in Figure 1, except for the I band where the error is much larger due to crowding⁴. These are, however, only indicative figures because the error distribution is very asymmetrical due to blending, an error of σ ≃ -0.2 mag being reached at J ∼ 28.5, K ≃ 27 and I ∼ 29. As a result, the output luminosity function is affected by an overall migration of objects from fainter to brighter bins, and in order to assess the feasibility of a science case, it is necessary to perform the whole test, proceeding, in our case, with the analysis of the output CMDs.

4.2. Comparison of CMDs

4.2.1. Disk galaxy at 4.6 Mpc

Figure 13 shows the input (Fig. 13a) and the output (Fig. 13b) CMDs for the young stellar population science case, with the diagnostic boxes superimposed. The characteristic plumes of the input CMD are well recognizable in the bright portion of the output diagram, but become progressively blurred towards fainter magnitudes. Three lines are drawn on the CMDs to distinguish three regimes: brighter than J ≃ 26.5 the main features of the CMD in Figure 13a are well reproduced in Figure 13b, including their narrow color width. Fainter than K ≃ 28 (slanted line) the stars' distribution in Figure 13b is completely dominated by the photometric errors, and presents no resemblance to the corresponding region in Figure 13a. In the range 26.5 ≤ J ≤ 28, the CMD in Figure 13b still retains the main features of the corresponding region in Figure 13a, but the color distribution of the stars is wider, showing that the photometric errors heavily affect the appearance of the CMD. Therefore, in order to derive the SFH from the analysis of this region of the CMD one needs to quantitatively account for the photometric errors. Note that this region includes the clump stars.

Zoom In Zoom Out Reset image size

Table 2 reports the star counts in the four diagnostic boxes in the input and output CMDs, showing that the counts are unaffected by the photometric error. Had we considered a more distant galaxy, or a stellar field with higher surface brightness, the diagnostic boxes would be closer to the confusion limit and the stellar blending would significantly affect the counts (starting from the RGB box, compare eq. [8] in Olsen et al. [2003]). This would result in a systematic error in the derived star formation. For the science case considered here, i.e., the central part of a disk galaxy at a distance of 4.6 Mpc, the diagnostic boxes are bright enough that the mass transformed into stars in the relative age ranges can be robustly derived. Note that the whole field of view of MICADO will be almost 20 times wider than simulated here, providing many stars for a robust statistics.

By applying the full synthetic CMD method to the simulated data in Figure 13, a more detailed SFH can be derived, in particular disentangling the contribution of the various age components in the range ∼1 to 12 Gyr. To this end, the HB/clump region may provide an effective diagnostic. The left panel of Figure 14 shows the input CMD in the clump region with stars color-coded according to their age bin. The different colors appear separated on the input CMD, where regions occupied by stars in different age bins can be distinguished: only objects older than 10 Gyr are found in the blue part of the horizontal-branch; stars with age between 1 and 2 Gyrs populate the faintest envelope of the clump, and the typical magnitude and color of core helium burning stars is a function of the age. Note that the various age components partially overlap, and it is not possible to construct clean diagnostic boxes similar to those used in the brightest part of the CMD. In addition, photometric errors substantially smear out the color distribution of the stars. The right panel of Figure 14 shows the same section of the output CMD with the detected objects color-coded according to their age. To build this diagram, we have assigned to each output source the age of its input star mate according to the position matching criterion. The smearing effect of the photometric error is readily apparent: the different age components of the stellar population are very hard to distinguish, so that the result of the application of the full synthetic CMD method will be very sensitive to the age binning and to the photometric errors.

Zoom In Zoom Out Reset image size

4.2.2. Elliptical galaxy at Virgo

Figure 15 compares the input and output CMDs for the old stellar population science case. The number of stars falling in the RGB box is 3538 in Figure 15a to be compared with the 3616 star counts in the same region of the CMD in Figure 15. Due to blending, some stars just fainter than the lower limit of the box become brighter and shift inside the box, contaminating the counts. However, the effect is quantitatively very small, and the total mass in stars can be recovered using the theoretical specific production within a few percent. Overall, the CMD of the detected sources appears very similar to the input CMD, especially brighter than J ≃ 28. Our aim is to check the impact of the photometric errors on a widely used method to derive the metallicity distribution of an old stellar population, which is based on the analysis of the CMD of bright RGB stars.

Zoom In Zoom Out Reset image size

Figure 15 shows the upper RGB of the input (Fig. 15a) and output (Fig. 15b) stellar lists, with the color encoding the metallicity bin. The [Fe/H] of each detected source is assigned equal to that of its input star mate on the image. The different metallicity bins appear well distinguishable in Figure 15b, especially in the upper 1.5 mag of the RGB. The derivation of the metallicity distribution from the analysis of the CMD is subject to uncertainties related to the age-metallicity degeneracy and to the AGB contribution to the counts in this part of the CMD (see, e.g., Rejkuba et al. 2011). Besides these systematic effects, the photometric errors introduce an additional uncertainty, which we evaluate here. We have selected from the output catalogue all the stars brighter than J = 28, and assigned to each of them a metallicity equal to that of the star in the input catalogue which has the closest position on the CMD. The difference between this value of [Fe/H] and that assigned from the source position on the image can be viewed as the error on the metallicity derived from the analysis of the CMD due to mere photometric errors. Figure 16 shows this difference as a function of the output magnitude in the J band, the two panels plotting the results from two different color combinations. The photometric errors introduce a mild uncertainty on the determination of [Fe/H] when using the (J, I - J) CMD: for most points the difference between the photometrically determined and the true metallicity is smaller than 0.1 dex. The error is larger when using the (J, J - K) CMD, as anticipated in § 2.2. Figure 17 illustrates the the impact of the errors on the photometrically derived metallicity distribution. The two histograms appear very similar: both peak at [Fe/H] ∼-0.2 and have similar widths and shape. We note that the photometrically-derived distribution is slightly overpopulated on the low metallicity side of the peak. Overall, however, the two distributions are very close to each other, and we conclude that this science case is well feasible in inner regions of giant elliptical galaxies at the distance of the Virgo Cluster.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

In this article we have explored the feasibility of two specific scientific applications for the study of the SFH in distant galaxies with the expected performance of a 42 m E-ELT equipped with the MICADO camera working close to the diffraction limit of the telescope. We have focused on giant galaxies located in the Centaurus Group and in the Virgo Cluster. These are regions of the nearby universe where a variety of galaxy types and morphology can be found, so that a significative sampling of the SFH in the universe can be gathered. In spite of the large collecting area of E-ELT, old MS turnoffs cannot be investigated at these distances; however, interesting information on the SFH can be derived from the analysis of the luminous portion of the CMD. The crucial advantage offered by the E-ELT working close to the diffraction limit is related to the exquisite spatial resolution that enables accurate photometry in crowded stellar fields. This will allow us to study the SFH in high surface brightness regions of giant galaxies where most of the stellar mass is located, and to address directly stellar population gradients, from the outskirts down to the inner regions of galaxies.

We have investigated how photometric errors impact on two science cases: (1) the study of the SFH at the center of the disk of a spiral galaxy at a distance of 4.6 Mpc (μ_B ≃ 21); (2) the recovery of the metallicity distribution in the inner regions (at half of the effective radius) in an giant elliptical galaxy at a distance of 18 Mpc (μ_I ≃ 19.6). To this end, we have produced synthetic frames in the I, J, and K bands by distributing theoretical stellar populations constructed with suitable star formation histories, and adopting the PSF currently foreseen for the MICADO camera assisted by the MAORY adaptive optics module. The synthetic frames were measured with a standard package for crowded fields photometry to yield output catalogues of detected stars. The input and output stellar lists have been compared to determine the photometric quality, and the output CMDs have been analyzed to assess to which extent the scientific aims of the two cases can be realized.

For both science cases, and in all photometric bands, blending of stellar sources leads to an asymmetrical error distribution, and a general migration of star counts along the luminosity function towards the brighter bins. Over a wide magnitude range, we detect an excess of stars recovered brighter than what they truly are, and the distributions of the (output—input) magnitude difference is more spread out on the negative (with respect to the positive) side. This effect becomes particularly relevant as one approaches the confusion limit, where stars are measured only if their luminosity is artificially boosted by blending (Greggio & Renzini 2011). At the same time, as the confusion limit is approached, a progressively larger incompleteness affects the luminosity function, partly balancing the excess due to blending. As a consequence, the measured luminosity function does not appear very different from the input one (see Figs. 9 and 12). Nevertheless, the asymmetry of the error distribution persists and can lead to misinterpretations of the CMD, e.g., distances from RGB tip (and HB) stars may be underestimated; too young ages may be inferred from main-sequence turnoff stars. Similarly, the age distribution from the core helium-burning/clump stars could be too skewed at the young end, and bright RGB stars overshooting the tip could be mistaken for relatively young AGB stars. Besides the systematic shift to brighter magnitudes of important diagnostic features, the asymmetry of the error distribution affects, in a systematic way, the star counts in the boxes used to derive the SFH. This effect, which is very important when trying to derive information from stars with a magnitude close to the confusion limit, may also hamper the results in less severe crowding conditions. Here we have checked that for our cases 1 and 2, the photometric accuracy is sufficient for their scientific aims.

Specifically, our results show that in the very central parts of disks of giant spirals located in the Centaurus Group (case 1):

• 1.  
  Accurate photometry (σ ∼ 0.1) can be obtained down to J ∼ 28.0 and K ∼ 27.0. At these magnitudes the luminosity functions are ≳90% complete.
• 2.  
  The characteristic plumes of the input CMD are very well reproduced in the output CMD down to J ∼ 26.5, and the star counts in bright diagnostic boxes which target specific age ranges are perfectly reproduced. This implies that the star formation history in the last ∼1 Gyr can be accurately derived, and that a robust estimate of the mass transformed into stars at ages older than ∼1 Gyr can be obtained from the star counts on the upper RGB.
• 3.  
  The analysis of the clump/HB stars to recover the SFH prior to ∼1 Gyr ago with a better age resolution requires the application of the full synthetic CMD method, which includes a careful modelling of the photometric errors. For the surface brightness considered, the smearing of the distribution of the clump stars is significant, hampering a robust solution. This case will be better performed in less crowded regions of disks.

The simulations of the case 2 stellar population shows that for giant ellipticals in the Virgo cluster:

• 1.  
  Accurate photometry (σ ∼ 0.1) can be obtained down to I ∼ 28.5 and J ∼ 27.5 at half of the effective radius (μ_B = 21.6). At these magnitudes the luminosity functions are ≳90% complete.
• 2.  
  The observed CMD well reproduces the width of the RGB in the upper 2 mag, and the color distribution of bright RGB stars is only mildly altered by the photometric errors, so that its interpretation in terms of metallicity distribution of the stellar population is only slightly affected. We estimate that the photometric errors introduce an uncertainty of ≃0.1 dex on [Fe/H] when using the I - J color combination as a tracer for the effective temperature.

Given the good photometric quality in the bright RGB region for science case 2, we argue that it will be possible to study the SFH in the central parts of disks in spiral galaxies in Virgo from star counts in bright boxes, as those shown in Figure 2. This will allow us to contrast the old (prior to ∼1 Gyr) to the more recent star formation activity over entire galaxies and across the Hubble sequence for all cluster members. The good photometric quality in the upper RGB will also allow us to derive the metallicity distribution almost all over giant galaxies, thereby tracing metallicity and population gradients.

For disks galaxies in the Centaurus Group, the analysis of the red clump/HB feature will provide a more detailed information on old star formation episodes. The central regions of disks appear too crowded for this purpose, but the results presented here have been obtained with a standard package for the photometry, which was not designed to work with such a structured PSF as the one provided by MAORY. Likely, the photometric accuracy will improve when using reduction packages more suitable for complex PSF that is produced by adaptive optics systems.

Further simulations that include a variable PSF shape over the whole field of view and other effects (nonhomogeneous background, field distortions, etc.) are required in order to fully characterize the capabilities of ELT imaging under different conditions. At the same time, simulations constructed with different choices for the stellar populations and crowding conditions are necessary to adequately explore the scientific return. These issues will be the subject of a forthcoming article.

We are indebted to G.P. Bertelli for computing the synthetic stellar populations used in our simulations. Preliminary results of this work are included in the Scientific Analysis Report document of the Phase A study of the MICADO camera. We thank R. Bedin and E. Held for their help in an early stage of this investigation, and A. Renzini for many useful discussions. This work was supported by funding of the phase A study of MICADO, and by Istituto Nazionale di Astrofisica funding 1.05.01.17.06.

The input lists of the synthetic stars were generated by random extractions of individual objects which belong to a library of theoretical simulations previously computed. For each of the two kinds of populations in Table 3, four simulations were constructed (G.P. Bertelli, private communication 2010) each constrained to have 200,000 objects brighter than a given magnitude M_K, max = +5, +1, -2 and -4. The brighter the magnitude limit, the more massive the simulated stellar population, and shorter-lived evolutionary phases become better sampled. Figures 2 and 4 show one of these mother simulations, respectively, for the young and for the old population.

The four mother simulations allow us to construct an input stellar list for young and/or old stellar populations of any prescribed size, since the number of stars in any region of the CMD is proportional to the total light (or total mass) of its parent stellar population. In particular, the number of stars with magnitude in a given range M_K,1 ≤ M_K ≤ M_K,2 is proportional to the total luminosity sampled. Therefore, once the size of the stellar population to be generated is given, e.g., its L_B through equation (1), the number of objects on its CMD with M_K,1 ≤ M_K ≤ M_K,2 is determined by scaling from the mother simulation of adequate depth, and the procedure is repeated to cover the whole magnitude range. The input stellar list is thus constructed by composing partial CMDs, each containing objects randomly extracted from the mother simulations. Note that the partial CMDs are limited in the K band because so are the original mother simulations. In the input stellar list each object is a synthetic star, i.e., characterized by mass, age, metallicity, and magnitude in all photometric bands.

In principle, the input list could contain stars down to M_K = +5, which is the limit of the deepest mother simulation. In practice, there is no need to generate a list down to the faintest magnitudes, which, unless the sampled luminosity is very low, would consist of an unmanageable large number of entries. Indeed, the stars on the synthetic frame will be measurable only down to some limiting magnitude function of the exposure time (for the given observational setup). Therefore, the stellar population on the frame is split into two components, i.e., individual stars brighter than M_K, lim, plus a pedestal of stellar light made of the stars fainter than this limit. The latter component is evenly distributed over the frame, with its Poisson noise.

Special care has been devoted to ensure completeness of the list of synthetic stars in all photometric bands, since this list is the input to generate frames at different wavelengths. The extraction procedure described above necessarily generates a list which is complete in the K band with the risk of undersampling the blue stars. Therefore, the value of M_K, lim is derived imposing completeness in the bluest band of the CMD to be constructed. In addition, the limiting magnitude for the input stellar list is chosen ∼1.5 mag fainter than the S/N = 5 level, to account for the effect on photometry due to stellar blending which leads to an artificial brightening of the sources.