Abstract
In the present study, the compressive strength of binary and ternary blended high-performance concrete mixtures was modeled using different machine learning tools, such as artificial neural network (ANN), gradient tree boosting (GTB), and multivariate adaptive regression splines (MARS). The compressive strength of binary and ternary blended concrete at 28 days of curing period was modeled using seven quantitative input parameters such as cement, blast furnace slag, fly ash, superplasticizer, water, coarse aggregate, and fine aggregate based on three different training and testing (Tr–Te) scenarios. The performance of the models developed was analyzed based on several statistical evaluation metrics, of error and efficiency. During the testing phase, the compressive strength estimates obtained via modeling using ANN, GTB, and MARS had Kling–Gupta efficiency (KGE) values of 0.8389, 0.8602, and 0.8423, respectively, for the first Tr–Te scenario; similarly, the KGE values were 0.8025/0.8830, 0.8541/0.8901, and 0.8434/0.8582, respectively, for the second/third Tr–Te scenarios. The estimation accuracy of the GTB model was relatively superior to that of the ANN and MARS models, taking into consideration both the error and efficiency indices. All three models perform relatively well for the first I/O combination compared to the other two combinations.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
High-performance concrete (HPC) is a 'future' material that has the potential to improve the durability of buildings and other infrastructure components (Neville and Aitcin 1998). Any characteristic of concrete can be linked to high performance in a wide sense. It can refer to excellent workability in the fresh state, such as self-compacting concrete, or low heat of hydration in mass concrete, or hardening of concrete in sprayed concrete for quick road and airfield repair, or concrete with very low imperviousness/leakage rates for storage vessels or material encapsulation containments. HPC is comprised of the same materials as conventional concrete, but it has been enhanced to meet the demands of a construction project. The basic components of high-performance concrete include cement, fine aggregate, water, coarse aggregate, chemical admixtures and mineral admixtures. Due to the material's complexity, simulating the behavior of high-performance concrete is an extremely challenging endeavor (De Larrard and Sedran 2002).
Even though concrete is the most widely used building material, it still has significant drawbacks, such as brittleness and poor tensile strength. HPC is a cutting-edge concrete technology with outstanding features such as high compressive and tensile strength, ductility, and durability. During the course of its intended service life, a concrete mixture with a high-performance rating provides suitable workability, develops high strength, and has remarkable durability characteristics. To achieve the above properties, ordinary concrete must be custom-made by lowering the water–cement ratio from 0.45 to 0.20, supplementing high-quality admixtures, and using water-reducing mineral admixtures as needed. Several industrial by-products are being used in concrete production as a substitute for cement or fine aggregate, or as an additive, to ensure environmentally friendly production for sustainable development (Chithra et al. 2016).
Concrete is the most often used construction material globally, with annual consumption exceeding 100 million cubic meters. Ordinary Portland cement concrete fails to meet a variety of functional standards, including demanding environments, construction time, energy absorption capacity, repair and retrofitting projects, and so on. As a result, there is a pressing need to produce high-performance concrete that is far superior to ordinary concrete. High-performance concrete is a type of concrete that has been engineered to have specified properties for a certain application and environment to deliver excellent performance in the structure in which it will be utilized. The term "high performance" refers to a set of structural properties that are well balanced in terms of strength, toughness, energy absorption capacity, stiffness, durability, multiple cracking resistance, and corrosion resistance, all while taking into account the material's final cost and, most importantly, the finished product.
“Special performance and uniformity requirements cannot always be met consistently by utilizing only conventional materials and nominal mixing and curing practices” according to the American Concrete Institute. Aspects such as installation and compaction without segregation, long-term mechanical properties, and early age strength or service life in difficult conditions all should be improved. Every feature of concrete can be linked to good performance in a broad sense (Priya and Sudalaimani 2019). To achieve these requirements, fly ash (from coal combustion), ground blast furnace slag (from steel production), silica fume (from high-quality quartz reduction in an electric arc furnace), rice husk ash (RHA), and various types of admixtures are widely utilized in high-performance concrete. Various amounts of these components are combined with Portland cement in varying percentages depending on the unique requirements for high-performance concrete (Yeh 1998).
In the past few decades, a great amount of effort has gone into developing high strength concrete, and the importance of this work is well informed. As long as the Portland cement itself is sufficient, the quality of the cement paste created in plain Portland cement concrete is widely regarded to be essentially an inverse function of the water–cement (w/c) ratio. To put it another way, the strength of concrete is determined by the overall void content of the material (Aitcin and Neville 1993). The HPC incorporates extra cementitious materials, such as fly ash, or blast furnace slag in addition to the three primary ingredients of regular concrete, namely Portland cement, fine and coarse aggregates, with water. But it is tough to predict the behavior of HPC because this is such a complex composite material.
Non-destructive evaluation of the compressive strength of high-performance concrete is a time-consuming, cumbersome, and exorbitant process. Usually, the empirical formulae developed employs various regression coefficients to describe the effects of various supplementary materials added to concrete. As a result, this raises doubts about the empirical formula's predictive power, given the very non-linear relationship between compressive strength of HPC and its constituents. Shafieifar et al. (2017) studied the tensile and compressive behavior of ultra high-performance concrete (UHPC) to develop a numerical model for simulating the behavior of the UHPC using the finite element (FE). The numerical analysis offered mechanical properties of UHPC in FE software utilizing the concrete damage plasticity model (CDP). In general, the computational and experimental results were in good agreement. Likewise, Bui et al. (2018) developed an expert system based on the artificial neural network (ANN) model in association with a modified firefly algorithm (MFA). The ANN model was built using experimental data, and MFA was used to increase the accuracy of this artificial intelligence technology by optimizing a set of initial weights and bias of ANN. The proposed expert system's accuracy was verified by comparing the acquired findings to those found in the literature. The results indicate that the MFA–ANN hybrid system can provide a better prediction of the high-performance concrete properties. Golafshani et al. (2020) developed gray wolf optimizer (GWO) combined artificial neural network (ANN) model, and adaptive neuro-fuzzy inference system (ANFIS) to construct prediction models for estimating the compressive strength of conventional concrete and HPC. They developed six ANN and three ANFIS models, using a dataset encompassing 2817 unique data records. The results show that hybridization of the GWO model improves the capacity of ANN and ANFIS models to offer generalized predictions. Earlier to this Erdal et al. (2013) showed the application of wavelet ensemble models for compressive strength predictions in high-performance concrete (HPC). Ensemble models namely the bagged artificial neural networks (BANN) and gradient boosted artificial neural networks (GBANN) were developed for this task. Coupling of discrete wavelet transform (DWT) with ANN ensembles for enhancing the prediction accuracy was also considered. The study suggests that DWT is a useful method for improving ANN ensemble accuracy. Later on, Han et al. (2019) showed that input variables and model parameters have a significant impact on the predictions from machine learning approaches with regard to high-performance concrete compressive strength prediction. Their research presented a two-stage strategy for selecting appropriate variables and simplifying parameter settings for predicting the compressive strength of HPC. The results suggest that the proposed method was effective for input variable optimization and can produce better predictions than those obtained without variable optimization. Similarly, Kaloop et al. (2020) used the multivariate adaptive regression splines (MARS) model (as a feature extraction method) to extract optimized inputs for designing the models of HPC. To predict compressive strength, a gradient tree boosting machine (GBM) was also used. Furthermore, a comparative study using various framework models (kernel ridge regression and Gaussian process regression) has been done to find their robustness. The data used for the estimation of compressive strength of HPC comprised of 1030 data sets of input variables such as cement, blasting slag, water, superplasticizers, fine aggregates, concrete age, etc. The results of the analysis show that each parameter's weights are relatively important during GBM calibration. Concrete age was found to be highly sensitive to predict the compressive strength among the six most influential parameters. Furthermore, the integrated MARS–GBM approach demonstrates a simplified approach for predicting compressive strength of HPC based on various evaluation metrics.
The greater the number of constituents, as well as the number of possible combinations, relative proportioning, and characteristics, the more difficult it is to predict the behavior of concrete. The majority of the researchers focused on material modeling, which involved developing mathematical models to describe the relationship between components and material behavior. They also investigated the use of neural networks to predict compression strength. One of the advantages of neural networks is their capacity to model highly non-linear data. When modeling a non-linear function, the MARS algorithm too has shown to produce results that are comparable to those of neural networks. MARS is capable of dealing with missing data, which is a common occurrence in large databases. Boosted tree models on all datasets can be more exact and interpretable than neural and non-linear networks, and gradient tree boosted models outperform other non-linear and neural systems. A study using multiple models of machine learning (neural, adaptive, and ensemble) to improve prediction precision is necessary for all these reasons. As a result, this research aims to predict the compressive strength of high-performance concrete using different machine learning models, namely the artificial neural network (ANN), gradient tree boosting (GTB), and multivariate adaptive regression splines (MARS) and compare the results.
2 Theoretical overview
Machine learning algorithms are systems that can self-learn complex patterns in data, forecast output, and enhance performance based on previous experiences. Based on the statistical relationship between input and output data and their extent/degree, algorithms work in a variety of ways. Understanding how different algorithms learn patterns, trends, and functions from given input data is critical. Knowing about algorithms allows us to select the best algorithm (or combination of algorithms) given the data at hand. The artificial neural network (ANN), gradient tree boosting (GTB), and multivariate adaptive regression splines (MARS) are the core topics of this research.
2.1 Artificial neural network (ANN)
Paradigms such as artificial neural networks are well suited to machine learning because connection weights and bias can be adjusted to improve a network's performance (Seyed and Javad 2013). A neural network is made up of simple processing units known as neurons. Normally, the neurons are grouped together logically into layers. There will be three or more layers within the network: the input layer, one or more hidden layers, and the output layer. Each neuron in a layer is linked to every other neuron in the layer adjacent to it. Each layer’s neurons communicate with neurons in other layers via weighted connections. The most common method is the trial-and-error approach, which is used to determine the ideal architecture of an ANN. If the number of hidden layers and their neurons are modified, the speed and accuracy of an ANN will also change (Kandiri and Fotouhi 2021). If the number of neurons in the hidden layer is too big or too small, it may result in over- or underfitting (Van Dao et al. 2020). By having the optimal weights and biases, the output of an ANN may be determined for any given pattern. Training the ANN in such a way that the disparities between anticipated and actual values are minimized yields the optimal weights and biases (Golafshani et al. 2020). Because the weights within the artificial neural network are modified after each iteration, this allows for a thorough learning process as well as generalized learning. The architecture of the ANN algorithm has an impact on its accuracy. As a result, the prediction error, as well as the ANN's complexity, should be considered as the two key objectives to be optimized in the challenge (Kandiri and Fotouhi 2021). One may find more information about ANN's algorithm and mathematical background at Keller and Priddy (2005) and Graupe (2013).
2.2 Gradient tree boosting (GTB)
One of the meta-algorithms in regression trees is the GTB approach (Khamehchi and Bemani 2021). A gradient boosting regression tree is a greedy algorithm that updates by minimizing a loss function’s estimated value. It is constructed in stages. The best model can be created by including several trees in the model; however, when the model's fit is too close to the training data, poor generalization ability can occur. During the training stage of the GTB algorithm, a decision tree is used to assign equal weight to each observation. The boosting process aids in the transformation of prediction from "weak" learner to "strong" learner through stage-wise additive training, and it is the underlying framework of this algorithm. GTB's main benefit is that it eliminates overfitting and uses less computational effort, thanks to its objective function. The loss function will be minimized in the training process. There are many loss functions used for regression problems such as “least squares”, “least absolute deviation”, “huber”, and “quantile” functions (Truong et al. 2020). Gradient Tree Boosting models have the best results due to optimized hyperparameter tuning. Some of them include estimators, maximum depth, minimum sample split, learning rate, and loss function. The gradient tree boosting (GTB) Python package was used in the research. One may find more information about GTB's algorithm and mathematical background at Friedman, (2001) and Ke et al., (2017).
2.3 Multivariate adaptive regression splines (MARS)
Friedman conceived the algorithmic logics of MARS method, a non-parametric regression strategy. Its algorithm is based on piecewise linear models aggregated via stepwise forward and backward procedure. To increase the prediction accuracy, the backward method removes extraneous variables from the previously selected set in the forward approach (Gholampour et al. 2020). It adopts a piecewise linear regression scheme to build models of non-linear relationship between predictand and predictor variables using a basis function (Cheng and Cao 2016). How the basis functions are selected is crucial in the MARS algorithm. There are two steps in this process: the forward stage, which is the growing or generation phase, and the backward stage, which is the pruning or refining phase. The pruning stage goes through each function one at a time and eliminates some that do not significantly improve the model's performance. A generalized cross-validation (GCV) score is used to do this. Furthermore, when a goal is the specified predictand variable, the non-linear relationship between predictor and predictand is easier to analyze. MARS is a more advanced version of classification and regression trees (CART), which was created to address the CART's flaws (Friedman 2007). MARS employs a divide-and-conquer technique, segmenting the training data sets into distinct zones, each with its own regression line (Shanmugapriya et al. 2018). One may find more information about MARS's algorithm and mathematical background at Friedman (2007) and Lewis and Stevens (1991).
3 Methodology
3.1 Data analysis
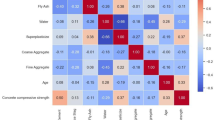
The dataset used for the modeling was collected from previous research paper (Yeh 1998). The dataset includes information of 1030 concrete specimens (Number of instances:1030, Number of Attributes: 9). These data are also available in UCI Machine Learning Repository: Concrete Compressive Strength Data Set (Yeh 2007). The seven parameters were used as inputs, namely the cement (kg/m3), blast furnace slag (kg/m3), fly ash (kg/m3), water (kg/m3), superplasticizer (kg/m3), coarse aggregate (kg/m3), fine aggregate (kg/m3) to model the compressive strength (MPa) of HPC at 28 days of curing. The entire dataset was classified into three categories/groups (A, B, and C). As shown in Table 1, machine learning tools were used for a variety of training and testing scenarios. The maximum, minimum, mean, standard deviation, co-efficient of variation, and kurtosis, the statistical properties of the data are tabulated in Table 2.
3.2 Model development
After analyzing the data, the data were imported to MATLAB for ANN modeling. The model was made to run for a different range of hidden layer neurons using the ANN code (from 3 to 10). The transfer functions were changed for finding the least error in prediction results, i.e., the least mean squared error for a specific number of hidden layer neurons, and the respective results were noted for all the combinations and further compared with each other, as presented in Table 3.
The GTB model parameters obtained during modeling are listed in Table 3. The models were optimized for “n estimators” ranging from 100 to 1000, “max depth” ranging from 2 to 10, “min samples split” tried for 2,4,6,8, and 10, “learning rates” of 0.1, 0.09, and 0.099, and loss functions—‘ls', ‘lad', and ‘huber'; where 'ls' stands for least squares and 'lad' stands for least absolute deviation, and huber loss functions.
The MARS model was optimized for the “max degree” with values ranging from 2 to 10, the “penalty” with values ranging from 0.3 to 0.8, “min_span alpha” and “end_span alpha” with values ranging from 0.04 to 0.06, and “end_span” with values ranging from 5 to 10. To discover the optimum combination of these hyperparameters that minimizes prediction error, we executed a grid search.
3.3 Performance evaluation
Statistical indices were used to assess the degree of agreement between predicted and actual data from ANN, GTB, and MARS models for all three combinations.
Mean absolute error (MAE)
Root mean squared error (RMSE)
Relative root mean squared error (RRMSE)
Normalized Nash–Sutcliffe efficiency (NNSE)
Willmott Index (WI)
Kling–Gupta efficiency (KGE)
where
where ‘Q’ denotes the observed value, ‘P’ indicates the predicted value, ‘\(\overline{P }\)’ mean of predicted data, ‘\(\overline{Q }\)’ mean of observed data, and ‘N’ represents the number of data points, ‘R’ signifies Pearson’s linear correlation co-efficient, ‘\({\sigma }_{P}\)’ refers to standard deviation of predicted values, ‘\({\sigma }_{Q}\)’ refers to the standard deviation of observed values.
4 Results and discussion
The compressive strength of HPC after 28 days of curing was modeled using machine learning tools such as ANN, GTB, and MARS with seven input parameters considering three training and testing combinations in the current study. Different statistical indices such as MAE, RMSE, RRMSE, NNSE, KGE, and WI were used to evaluate the performance of the models.
4.1 First I/O combination:
The goal was to accurately estimate the compressive strength of HPC using multiple machine learning algorithms, such as ANN, GTB, and MARS. The experimental data samples were separated into two groups: training and testing. The data groups B and C were used as the training dataset, whereas group A was used as the testing dataset. About 35 percent of the data was used as a testing set (140 samples), while the remaining 65 percent was used as a training set (285 samples). Table 4 shows the simulated outcomes from three predictive models for both the training and testing phase. It is obvious that all models in the training stage showed impressive accuracy, with the GTB model producing the highest WI (0.9996) and the lowest values of MAE (0.1579 MPa), RMSE (0.567 MPa), and RRMSE (0.0386). The testing phase, on the other hand, is critical in determining the generalization performance of prediction models. The superiority of GTB over other models was seen during the testing process, as shown in Table 4. Furthermore, with the least magnitudes of MAE (3.5789 MPa), RMSE (5.3785 MPa), RRMSE (0.3634), and the higher value of WI (0.9613), the GTB model predicted compressive strength values with the highest accuracy.
Several graphical visualizations, like scatter plots, violin plots, and Taylor diagrams, were constructed to more rigorously analyze the performance of each developed model throughout the testing phase. A scatterplot (also known as a correlation diagram or a scattergram) depicts the relationship between two sets of data (i.e., observed v/s predicted). Figure 1 shows the scatter plots of individual models for the first I/O combination with a positive correlation. From the figure, it is evident that the ANN, GTB, and MARS have predicted data with a co-efficient of determination of 0.7886, 0.8670, and 0.8094 respectively, as against the observed values.
The violin plot pools the elite statistical features and augments the fundamental summary statistics inherent in box plots with the information provided by local density estimates. This combined summary statistics and density shape in a single plot serves as a useful tool for data analysis and exploration. Figure 2 shows the violin plot for the first combination. This gives a way for the comparison of all three model performances. On each side of the Greyline is a kernel density estimation to show the distribution shape of the data. Looking into the plots, the distribution of GTB has a more similar widening as witnessed with respect to observed compressive strength data.
For better visual comparison, the Taylor diagram was constructed since it can summarize several statistical indices (correlation co-efficient, RMSD, and standard deviation) in one visual and consequently aid in the process of picking the optimal model. Taylor diagrams are a visual representation of how well a data pattern (or a set) matches the observations. The similarity between two data patterns is computed in terms of their centered root-mean-square difference, correlation, and standard deviations. Figure 3 shows Taylor’s diagram which summarizes how relative the prediction values lie in connection with observed values. From visual analysis, the GTB model performance is superior compared to the ANN and MARS models.
4.2 Second I/O combination
The training dataset comprised of groups C and A, while the testing dataset considered was group B in this I/O combination. According to the statistical results in Table 5, the GTB model performed well during the training phase, achieving greater WI (0.9998) and the lowest RRMSE (0.0307) value. In the testing phase too, better results were obtained from the GTB model than the other two models, with greater WI (0.936) and lower MAE (4.4051 MPa) value. Figure 1 shows the scatter plots of all models for the second I/O combination with a positive correlation. From the figure, it is evident that ANN, GTB, and MARS have predicted with a co-efficient of determination of 0.7899, 0.7771, and 0.7919, respectively, as against the observed values. However, in this combination, MARS model provided similar prediction efficiency as that of GTB model. Looking into the violin plot, the distribution of GTB was more like that of the observed data (Fig. 4). For detailed comparisons, Taylor’s diagram as shown in Fig. 5, summarizes how relative is the prediction values lie with respect to observation values. From visual analysis, it is proven that both GTB and MARS have provided relatively similar predictions.
4.3 Third I/O combination
In this case, data groups A and B were used as the training dataset, whereas group C was used as the testing dataset in this I/O combination. Each model performance for this I/O combination is tabulated in Table 6. The ANN and MARS models had the similar accuracy in prediction in terms of MAE (4.8404 MPa and 4.9814 MPa), RMSE (6.6067 MPa and 7.6886 MPa), and RRMSE (0.4493, and 0.5229), respectively. The GTB model, on the other hand, had the best prediction accuracy, with very low MAE (3.5402 MPa), RMSE (5.3066 MPa), and RRMSE (0.3609), as well as greater NNSE (0.8841), KGE (0.8901), and WI (0.9633) values. Although statistical indicators show a high degree of confidence in the prediction of compressive strength data from the three models, graphical evaluation is essential. Figure 1 shows the scatter plots of each individual model predictions for the third combination with a positive correlation. From the figure, it is seen that ANN, GTB, and MARS have predicted with a co-efficient of determination of 0.7967, 0.8689, and 0.7247, respectively, as against the observed values. Hence in this I/O combination, again GTB has better prediction efficiency than the other two models. Figure 6 shows the violin plots for the third I/O combination. Looking into the plot, the distribution of GTB has a more or less similar widening as that of the observed data. The violin plot of MARS predicted data showed varied skew, symmetry, and shape characteristics. Figure 7 shows Taylor’s diagram which summarizes how relative the prediction values lie with respect to observation values. Here again, the GTB model predictions were superior in terms of all three statistical indices of Taylor Diagram.
5 Conclusions
In the present study, simple, advanced and ensemble machine learning approaches namely the ANN, MARS and GTB were applied to model the compressive strength of high-performance concrete using seven input parameters considering three different training and testing combinations. Based on the results obtained, all three models performed better for the first I/O combination compared to the other two combinations. The GTB model provides superior predictions in comparison with ANN and MARS in all three I/O combinations. Parameter optimization played a major role in the model development process and has significant impact on the model outputs.
Availability of data and materials
The data are made available in the supplementary file.
References
Aitcin PC, Neville AM (1993) High-performance concrete demystified. Concr Int 15:21–26
Bui DK, Nguyen T, Chou JS, Nguyen-Xuan H, Ngo TD (2018) A modified firefly algorithm-artificial neural network expert system for predicting compressive and tensile strength of high-performance concrete. Constr Build Mater 180:320–333. https://doi.org/10.1016/j.conbuildmat.2018.05.201
Cheng MY, Cao MT (2016) Estimating strength of rubberized concrete using evolutionary multivariate adaptive regression splines. J Civ Eng Manag 22(5):711–720. https://doi.org/10.3846/13923730.2014.897989
Chithra S, Kumar SRRS, Chinnaraju K, Alfin Ashmita F (2016) A comparative study on the compressive strength prediction models for high performance concrete containing nano-silica and copper slag using regression analysis and artificial neural networks. Constr Build Mater 114:528–535. https://doi.org/10.1016/j.conbuildmat.2016.03.214
De Larrard F, Sedran T (2002) Mixture-proportioning of high-performance concrete. Cem Concr Res 32(11):1699–1704
Erdal HI, Karakurt O, Namli E (2013) High performance concrete compressive strength forecasting using ensemble models based on discrete wavelet transform. Eng Appl Artif Intell 26(4):1246–1254. https://doi.org/10.1016/j.engappai.2012.10.014
Friedman JH (2001) Greedy function approximation: a gradient boosting machine. Ann Stat 29(5):1189–1232. https://doi.org/10.1214/aos/1013203451
Friedman JH (2007) Multivariate adaptive regression splines. Ann Stat. https://doi.org/10.1214/aos/1176347963
Gholampour A, Mansouri I, Kisi O, Ozbakkaloglu T (2020) Evaluation of mechanical properties of concretes containing coarse recycled concrete aggregates using multivariate adaptive regression splines (MARS), M5 model tree (M5Tree), and least squares support vector regression (LSSVR) models. Neural Comput Appl 32(1):295–308. https://doi.org/10.1007/s00521-018-3630-y
Golafshani EM, Behnood A, Arashpour M (2020) Predicting the compressive strength of normal and high-performance concretes using ANN and ANFIS hybridized with Grey Wolf optimizer. Constr Build Mater 232:117266. https://doi.org/10.1016/j.conbuildmat.2019.117266
Graupe D (2013) Principles of artificial neural networks, 3rd edn. World Scientific Publishing Company, Singapore
Han Q, Gui C, Xu J, Lacidogna G (2019) A generalized method to predict the compressive strength of high-performance concrete by improved random forest algorithm. Constr Build Mater 226:734–742. https://doi.org/10.1016/j.conbuildmat.2019.07.315
Kaloop MR, Kumar D, Samui P, Hu JW, Kim D (2020) Compressive strength prediction of high-performance concrete using gradient tree boosting machine. Constr Build Mater 264:120198. https://doi.org/10.1016/j.conbuildmat.2020.120198
Kandiri A, Fotouhi F (2021) Prediction of the module of elasticity of green concretes containing ground granulated blast furnace slag using hybridized multi-objective ANN and Salp swarm algorithm. J Constr Mater 2(2):1–19. https://doi.org/10.36756/jcm.v2.2.2
Ke G, Meng Q, Finley T, Wang T, Chen W, Ma W, Ye Q, Liu T -Y. (2017). LightGBM: a highly efficient gradient boosting decision tree. 31st Conference on neural information processing systems (NIPS 2017), Long Beach, CA, USA. 3147–3155. https://proceedings.neurips.cc/paper_files/paper/2017/file/6449f44a102fde848669bdd9eb6b76fa-Paper.pdf
Keller PE, Priddy KL (2005) Artificial neural networks: an introduction. SPIE Press, United States
Khamehchi E, Bemani A (2021) Prediction of pressure in different two-phase flow conditions Machine learning applications. Meas J Int Meas Confed 173:108665. https://doi.org/10.1016/j.measurement.2020.108665
Lewis PAW, Stevens JG (1991) Nonlinear modeling of time series using multivariate adaptive regression splines (MARS). J Am Stat Assoc 86(416):864–877. https://doi.org/10.1080/01621459.1991.10475126
Neville A, Aitcin PC (1998) High performance concrete—an overview. Mater Struct 31:111–117
Priya C, Sudalaimani S (2019) Properties of fiber reinforced high performance concrete-a case study. Int J Eng Res Technol 8(02):123–131. https://doi.org/10.17577/IJERTV8IS020074
Seyed HMJ, Javad A (2013) Simulation of circular jet outfalls using artificial neural network. Int J Phys Sci 8(20):1099–1110. https://doi.org/10.5897/ijps12.254
Shafieifar M, Farzad M, Azizinamini A (2017) Experimental and numerical study on mechanical properties of ultra high performance concrete (UHPC). Constr Build Mater 156:402–411. https://doi.org/10.1016/j.conbuildmat.2017.08.170
Shanmugapriya T, Uma RN, Murali K (2018) Multivariate adaptive regression splines model to predict strength characteristics of high performance concrete. J Struct Eng (india) 45(3):231–239
Truong VH, Vu QV, Thai HT, Ha MH (2020) A robust method for safety evaluation of steel trusses using gradient tree boosting algorithm. Adv Eng Softw 147(March):102825. https://doi.org/10.1016/j.advengsoft.2020.102825
Van Dao D, Adeli H, Ly HB, Le LM, Le VM, Le TT, Pham BT (2020) A sensitivity and robustness analysis of GPR and ANN for high-performance concrete compressive strength prediction using a monte carlo simulation. Sustainability 12(3):830. https://doi.org/10.3390/su12030830
Yeh I-C (1998) Modeling of strength of high-performance concrete using artificial neural networks. Cem Concr Res 28(12):1797–1808. https://doi.org/10.1016/S0008-8846(98)00165-3
Yeh I-C (2007) Concrete compressive strength. UCI Mach Learn Repository. https://doi.org/10.24432/C5PK67
Acknowledgements
The authors would like to thank the Department of Civil Engineering, Siddaganga Institute of Technology, Tumakuru for the necessary infrastructural support.
Funding
Open access funding provided by Manipal Academy of Higher Education, Manipal.
Author information
Authors and Affiliations
Contributions
SBM, SRN: Conceptualization, Methodology, Supervision; MNM, KAS: Modeling, Validation, Verification, Writing—Original Draft. SRN: Writing Review and Editing. All authors have read and approved the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors confirm that there are no conflicts of interest associated with this publication.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Murthy, M.N., Amruth, S.K., Marulasiddappa, S.B. et al. Modeling the compressive strength of binary and ternary blended high-performance concrete mixtures using ensemble machine learning models. Soft Comput 28, 6683–6693 (2024). https://doi.org/10.1007/s00500-023-09521-x
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-023-09521-x