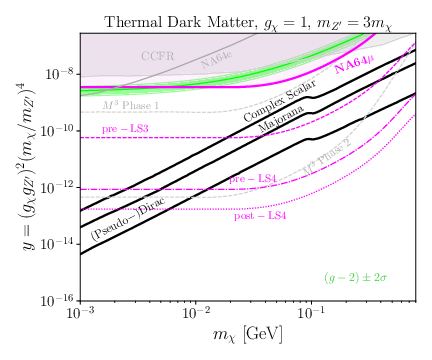
| The NA64$\mu$ 90\% C.L. exclusion limits in the parameter space compatible with a light boson as an explanation for the muon $(g-2)_\mu$. Left: The $Z'$ vector boson parameter space $(m_{Z'},\ g_{Z'})$ together with existing constraints from neutrino experiments such as BOREXINO \cite{Kamada:2015era,Kaneta:2016uyt,Gninenko:2020xys} and CCFR \cite{Altmannshofer:2014pba,CCFR:1991lpl}, visible searches in electron-positron annihilation with BaBar \cite{Capdevilla:2021kcf}, Belle II constraints \cite{Belle-II:2019qfb} and the NA64 electron program limits \cite{Andreev:2024lps}. Projections for the pre-LS3, pre-LS4, and post-LS4 phases of the muon program are shown together with the $M^{3}$ missing momentum searches \cite{Kahn:2018cqs}. Right: The $S$ scalar boson parameter space $(m_{S},\ g_{S})$ together with existing constraints from BaBar and projections for the pre-LS3, pre-LS4, and post-LS4 phases of the muon program, as well as ATLAS HL-LHC \cite{Galon:2019owl} and $M^{3}$. |