磁気の波とトポロジー – 「波」を抽象的数学でひも解く
実体波と境界波
身近な「波」といえば、水の波紋があります。それを例に話を始めます。水が静かに満ちている洗面器の壁面近くの水面を指先で揺らすと波が立ちますね。その波は指先から同心円状に水面全体に広がっていくでしょう。このように、波源から媒質(この場合水面)の全方向に伝わる波を「実体波」と呼びます。ではもしも、波が洗面器の中心に向けては広がらず壁面との境界に沿ってだけ伝わったとしたら、これは不思議です。
日常生活でこのような例を見ることはほとんどないですが、たとえば地震波(地面を媒質として振動が伝わる波)では震源から地球の中心に向かわず大気との境界に沿ってだけ伝わる場合があることが知られており、これを「境界波」と呼びます。どんな波も必ず実体波を持ちますが、境界波はいつでもあるとは限りません。

なぜ境界に沿ってだけ振動が伝わることが可能なのでしょうか? 境界そのものに何か仕掛けがあると考えるのが自然ではないかと思います。ところが近年、波が境界波を持つか否かは境界の性質には無関係で、むしろ実体波の性質でほぼ完全に決まってしまう例が多数見つかりました。
波が境界に沿って伝わることができるかどうかを知るには境界から離れた部分を伝わる波だけを調べれば良い、と言うのです。しかもその根拠はとても抽象度の高い数学「トポロジー」にあって、結果としてこの手の境界波は実体波より減衰しにくいことが保証されます。
おもしろいと思いませんか? 今回紹介する研究では、このトポロジーに基づく実体波と境界波の関係が、磁気の波に対しても成り立っていることを明らかにしました。
磁気の波とは?
この記事では、「波」という言葉を周期振動が伝播する現象という意味で使うことにします。洗面器の水の例では波源で水面の高さが周期的に時間変化し、それが徐々に空間的に広がります。このとき、水面の各点は波源と同じ周期で振動しています。また振動が伝わるには時間がかかるため波源から離れるほど振動に遅れが出て、結果として水面の高さに山谷のパターンができます。隣り合う山の間の距離を波長と呼びます。
波の周期と波長には一定の関係があり、この関係は媒質によって異なります。さまざまな波(たとえば水の波と地震波)の性質の違いは、この周期と波長の関係の違いとして表すことができます。
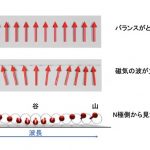
冷蔵庫に貼ってある普通の磁石にも、目には見えない磁気の波を立てることができます。磁石は無数のミクロな棒磁石が一方向にそろって並んでできています。

それぞれの棒磁石がつくる磁場が、隣り合う棒磁石を押し合うことでバランスを保っていますが、どれかひとつを揺らすとバランスのとれた状態に戻ろうとする復元力で振動を始めます。この振動の広がりが「磁気の波」です。もちろんそれは水の波とも地震波とも異なる周期と波長の関係を持っています。

磁気の波は昔から知られていましたが、近年、磁石に微細な加工を加えることで波の性質を変えたり、微弱な光や電流によって波を立てて制御できることがわかってきました。ナノテクノロジーの発展で、磁気の波を情報機器の省エネルギー化に応用する可能性が拓けてきたことが本研究の動機のひとつとなっています。
磁気の境界波はなぜ減衰しにくいのか?
実は、磁気の波にも境界波があることは古くから知られていました。しかもこの境界波は、磁気の波の実体波と比べて非常に減衰しにくいことが実験によりわかっています。この特別な性質のために、磁気の波に関する研究の多くは境界波を対象としています。しかし、盛んに研究されているにも関わらず、「なぜ磁気の境界波が実体波より減衰しにくいか」について、明確な説明を与えた人はいませんでした。
ここで波が減衰する原因は何かについて少し考えてみましょう。それは大雑把に言って、波が他の波にエネルギーを奪われていくからです。水の波が障害物に当たれば別の波長を持つ波に一部変換されて、それが繰り返されることでさまざまな波長を持った小さな波の重ね合わせとなり、元の波の方は消えていきます。
障害物がなくても、水の波は水分子のミクロな運動などにエネルギーを渡して減衰します。量子力学によれば、この分子運動もある種の波であって周期と波長を持っています。このとき、元の波とエネルギーを奪う波の周期や波長が大きく異なっていると、エネルギーを受け渡す効率が悪くなり減衰しにくくなります。このことから、波の減衰を抑えるためには、その波の周期と波長に近い波を環境から可能な限り排除してしまえば良いということになります。
実体波のギャップとトポロジー
波の性質は周期と波長の関係で決まると述べました。波長を連続的に変化させると周期もある範囲を動くわけですが、どのように波長の値を選んでもある範囲の周期を持った波を立てることができないことがあります。この波が伝播できない範囲を「ギャップ」と呼びます。
もしもこのギャップに含まれている周期の値を持った波を立てることができれば、近い周期を持った他の波がいないわけですから減衰が抑えられた状況を作ることができます。ただ、波を立てられない周期を持った波を立てる、と言うと矛盾していますね。でも、実体波のギャップに境界波を立てるというのではどうでしょうか?
主に今世紀に入って以降、画期的な発見が連続し、「実体波のトポロジー」に着目するとまさにそのギャップに境界波が現れる状況が起こり得ることが明らかにされてきました。
トポロジーとは何でしょうか? 実用上の一側面だけ切り取れば、それは数学的対象に整数を割り振るルールです。数学的対象の例として曲面をとってみましょう。身の回りにあるあらゆるものの表面が数学的には曲面であると考えることができます。その形や大きさ、材質などはさまざまですが、それらとは無関係に曲面に幾つ穴が空いているかを数えることで、各曲面に整数を割り振ることができます。これがトポロジーの最も有名な応用例ですが、本来は非常に抽象的で一般的な概念であるため、およそどのような数学的対象にも適用できます。

実体波の周期と波長の関係は、まさに数学的対象だと見なすことができます。そして、実体波の周期にギャップがある場合には与えられた周期と波長の関係から整数を計算することができます。これが、実体波のトポロジーです。もしこの整数がゼロでなければ、その媒質の端には必ず境界波が存在し、しかもその周期は実体波のギャップ中にあることが(適当な条件の下では)数学的に言い切れます。この驚くべき結果を数学を使わずに説明することは、残念ながら私にはできません。
私たちは磁気の実体波が持つ周期と波長の関係から整数を計算することができ、その値が実際にゼロでないということを明らかにしました。このとき問題となったのは、磁気の実体波には通常ギャップがないと考えられている点で、ギャップの意味を磁気の波に合わせた形で再定義する必要がありました。これらにより、古くから知られた磁気の境界波が実は実体波のトポロジーの産物であって、それが減衰しにくさの根本原因であることをはじめて突き止めることができました。
終わりに
実体波のトポロジーから境界波が存在するか言い切れる、と書きましたが、実は数学的に厳密な証明があるのはごく限られた場合だけです。しかし物理学の方からは、この実体波と境界波の対応が、数学的な証明の範囲を超えて幅広く成立していることを示唆する証拠が積み上がりつつあります。
一方物理的にもまだ謎が多くあります。たとえば、地震波の境界波はトポロジーと関連があるのでしょうか? 私の知る限りではこの問題に対する回答はまだありません。「波」というありふれた現象と抽象的数学が結びついて、今も新しい知を生み出し続ける様子の一端が、少しでも読者の方々に伝われば幸甚です。
参考文献
Kei Yamamoto, Guo Chuan Thiang, Philipp Pirro, Kyoung-Whan Kim, Karin Everschor-Sitte, and Eiji Saitoh “Topological Characterization of Classical Waves: The Topological Origin of Magnetostatic Surface Spin Waves” Phys. Rev. Lett. 122, 217201 (2019)
DOI:https://doi.org/10.1103/PhysRevLett.122.217201
この記事を書いた人

-
日本原子力研究開発機構 先端基礎研究センター 任期付研究員。
京都大学理学部卒業後、ケンブリッジ大学でPhD(応用数学)取得。神戸大学、マインツ大学、アラバマ大学で研究員を務めたのち、2018年1月から文部科学省卓越研究員制度を利用して現職。主に磁性と物質中の角運動量の流れに関連する多様な物理現象の背後にある数理構造を明らかにすることを興味の中心として研究に従事。
この投稿者の最近の記事
 研究成果2019.09.24磁気の波とトポロジー – 「波」を抽象的数学でひも解く
研究成果2019.09.24磁気の波とトポロジー – 「波」を抽象的数学でひも解く