Pythonによる機械学習の最前線
•
127 likes•81,586 views
2016/2/4 「ソフトウェアジャパン ビッグデータ活用実務フォーラム」でのプレゼン資料です。 主にPythonで書いたコードの高速化の話です。タイトルと中身がマッチしない感じがするのは自覚しています。
![ベンチマーク例
def prime(n):
p = [True] * (n + 1)
m = 2
while m < n + 1:
if p[m]:
i = m * 2
while i < n + 1:
p[i] = False
i += m
m += 1
i = n
while not p[i]:
i -= 1
return i
n以下の最大の素数を返す関数
（エラトステネスのふるい）
通常のPython版：4.75秒 Cython化版：3.04秒
prime(10000000)を計算
（コードには手を入れず）](https://image.slidesharecdn.com/2016-160204123707/85/Python-21-320.jpg)
![def prime(int n):
cdef int i, m
p = [True] * (n + 1)
m = 2
while m < n + 1:
if p[m]:
i = m * 2
while i < n + 1:
p[i] = False
i += m
m += 1
i = n
while not p[i]:
i -= 1
return i
def prime(n):
p = [True] * (n + 1)
m = 2
while m < n + 1:
if p[m]:
i = m * 2
while i < n + 1:
p[i] = False
i += m
m += 1
i = n
while not p[i]:
i -= 1
return i
型宣言をいれる
3.04秒 0.41秒](https://image.slidesharecdn.com/2016-160204123707/85/Python-22-320.jpg)
![def prime(int n):
cdef int m, i
cdef int * p = <int * >malloc((n + 1) * sizeof(int))
for i in range(n + 1):
p[i] = 1
m = 2
while m < n + 1:
if p[m]:
i = m * 2
while i < n + 1:
p[i] = 0
i += m
m += 1
i = n
while not p[i]:
i -= 1
free(p)
return i
0.41秒 0.17秒
リスト（配列）についてもC言語風の型宣言と動的割当て](https://image.slidesharecdn.com/2016-160204123707/85/Python-23-320.jpg)
Pythonによる機械学習の最前線
- 2. 自己紹介 加藤公一（かとうきみかず） シルバーエッグ・テクノロジー（株） 博士（情報理工学） （修士は数理科学） Twitter: @hamukazu 機械学習歴・Python歴ともに3年 今の仕事： 機械学習に関する研究開発 特にレコメンデーション（自動推薦）システム、自然言語処理、画 像処理など 過去の仕事： データ分析ツールの開発、3次元CADの開発、幾何計 算のアルゴリズム設計、偏微分方程式のソルバなど
- 3. Pythonで使える 機械学習・データ分析のツール • 汎用数値計算、科学技術計算：Numpy, Scipy • 機械学習：scikit-learn • 自然言語処理：nltk • データ分析：pandas • データ可視化：matplotlib • 統合分析環境：jupyter-notebook
- 4. Pythonで使える ディープラーニングのライブラリ • Pylearn2 • Caffe • TensorFlow • Chainer
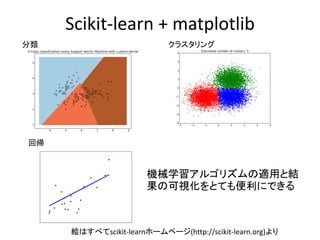
- 5. Scikit-learn + matplotlib 分類 クラスタリング 回帰 機械学習アルゴリズムの適用と結 果の可視化をとても便利にできる 絵はすべてscikit-learnホームページ(http://scikit-learn.org)より
- 7. 可視化応用編 • さらにインタラクティブな可視化をしたいとき – 例えば… • クリックした部分だけ拡大したい • マウスオーバーすると詳細情報を表示したい • そういうときはPython+JavaScriptが便利 • Pythonでアプリケーションサーバを立ち上げるの は簡単 – Bottle、Flaskなどの軽量フレームワーク – サーバと連携してのJavaScriptでの可視化 • ウェブアプリの仕組みはデータ分析にも有用
- 10. スクリプト言語とは 「アプリケーションソフトウェアを作成するための簡 易的なプログラミング言語の一種を指す」 -- Wikipedia Perl, Ruby, Pythonなど 特徴： • 短い行数で（少ないタイプ数で）書ける – つまり生産性が高い – 初心者が学習しやすい • インタプリタ型である • 実行速度が遅い
- 11. 注意：Pythonは汎用言語です！ 数学的用途以外にも使えます。 • ウェブアプリ作ったり • ゲーム作ったり • ツイッターのボット作ったり • ラズベリーパイからLED光らせたり もできます。 でも今日はその話はしません。
- 12. 数値計算・数学的アルゴリズムで Pythonを使うべき理由 • ライブラリが充実 • 結果の可視化が便利 • （うまくコードを書くと）速い⇨以降この話 数値計算、アルゴリズム系の人、 「Pythonは遅いからイヤ」と思ってる人が多いの では？
- 13. Pythonでやってはいけないこと s = 0 for i in range(1, 100000001): s += i print(s) 1から1億までの和を計算する これはPython的な書き方ではない
- 14. 改善例 s = sum(range(1, 100000001)) print(s) 1から1億を返すイテレータを用意し、その和を計算する
- 15. Numpyを使う import numpy as np a = np.arange(1, 100000001, dtype=np.int64) print(a.sum()) 1から1億が入った配列を用意し、その和を計算する
- 16. ベンチマーク s = 0 for i in range(1, 100000001): s += i print(s) s = sum(range(1, 100000001)) print(s) 30.21秒 12.33秒 0.38秒 import numpy as np a = np.arange(1, 100000001, dtype=np.int64) print(a.sum())
- 17. 問題点（？） • Numpy版は1～100000000が入った配列をあ らかじめ用意している • つまりメモリが無駄 • メモリにデータを入れるコストも無駄 ⇨Pythonistaはそんなこと気にしない！
- 18. ここまでのまとめ • Pythonの数値計算系ライブラリはC言語等で書 かれているので速い • できるだけ計算はライブラリに任せたほうがいい • ライブラリとのやり取りを大量にするより、一度ラ イブラリに仕事を投げたらしばらく返ってこないく らいの処理がよい – Numpyには高速化のための仕組みがたくさんある （indexing, slicing, broadcasting, etc…） • そのためにメモリ量やメモリコピーコストがか かっても気にしない
- 19. でもそれができないときがある • ライブラリ内ではなく、Python側で条件分岐が 大量に必要になる場合 • どうしてもfor文（while文）で細かい処理をたく さん回さなければいけないとき • 例えば探索系アルゴリズム、組み合わせ最 適化など
- 20. そんなときに… Cython • PythonをベースにしたC言語のジェネレータ • Pythonで書いたものをそのまま速くすること ができる • ちょっと手を入れることでさらに速く
- 21. ベンチマーク例 def prime(n): p = [True] * (n + 1) m = 2 while m < n + 1: if p[m]: i = m * 2 while i < n + 1: p[i] = False i += m m += 1 i = n while not p[i]: i -= 1 return i n以下の最大の素数を返す関数 （エラトステネスのふるい） 通常のPython版：4.75秒 Cython化版：3.04秒 prime(10000000)を計算 （コードには手を入れず）
- 22. def prime(int n): cdef int i, m p = [True] * (n + 1) m = 2 while m < n + 1: if p[m]: i = m * 2 while i < n + 1: p[i] = False i += m m += 1 i = n while not p[i]: i -= 1 return i def prime(n): p = [True] * (n + 1) m = 2 while m < n + 1: if p[m]: i = m * 2 while i < n + 1: p[i] = False i += m m += 1 i = n while not p[i]: i -= 1 return i 型宣言をいれる 3.04秒 0.41秒
- 23. def prime(int n): cdef int m, i cdef int * p = <int * >malloc((n + 1) * sizeof(int)) for i in range(n + 1): p[i] = 1 m = 2 while m < n + 1: if p[m]: i = m * 2 while i < n + 1: p[i] = 0 i += m m += 1 i = n while not p[i]: i -= 1 free(p) return i 0.41秒 0.17秒 リスト（配列）についてもC言語風の型宣言と動的割当て
- 26. まとめ • Pythonには数値計算、機械学習、データ分析 に便利なライブラリがそろっている • Pythonはうまくつかうとかなり速い – できるだけ仕事はまとめてライブラリに任せる – それができないときはCythonを使う – Cythonならではの工夫（型宣言）などが必要