地味にここ5年間ぐらい、マルコフ連鎖モンテカルロ法(MCMC)が流行っているようです。汎用的な分布でベイズ推定を行う時に有用な数値解析アルゴリズムの総称で、Metropolis-Hastings algorithm(M-Hアルゴリズム)などが主要なメソッドとして使われています。ただし、ベイズ推定以外でも利用する事はできます。
RでもMCMCpackと言うパッケージがあるのですが、取扱説明書を見る限り、ベイズ推定が前提となっておりM-Hアルゴリズムだけを試すことは難しそうです(追記:MCMCmetrop1R()関数で利用できます)。もっとも同アルゴリズムは比較的シンプルなモノなので、ポアソン分布から乱数を作成し、それを推定する練習をしてみました。
1. ポアソン分布からλ=1の乱数を作成
ポアソン分布からλ=1の乱数を作成します。練習のためにポアソン分布を利用したのは、推定するパラメーターがλ一つとシンプルな為です。正規分布でも平均μと分散θの2パラメーターになるので、ポアソン分布より簡単な分布は無いでしょう。
# 再現性を持たすため、乱数のシードを設定
set.seed(1631697)
# λ=1とする
lambda <- 1
# ポアソン分布の乱数を作成
x <- rpois(100, lambda)
乱数を作成するだけではなく、出現頻度も確認しておきましょう。
# 分布を見てみる
xtabs(~x)
サンプルの分布は以下のようになります。ポアソン分布ですね。
| 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 43 | 37 | 14 | 5 | 1 |
2. 最尤法(ニュートン=ラフソン法)で推定してみる
サンプルからnlm()関数を用いて最尤法でλを推定してみます。λは0.84000(mean(x)と等しいので正しい値)、分散は0.00840となっています。また、7回の繰り返しで収束しています。
# ポアソン分布の対数尤度関数mlpoiを定義
# nlm()関数の都合で符号は逆
mlpoi<-function(p){
-(sum(x*log(p))-length(x)*p-sum(log(factorial(x))))
}
# 最尤法(ニュートン=ラフソン法)
r_ml <- nlm(mlpoi, 0.5, hessian=TRUE)
# 推定結果を表示
print(sprintf("lambda:%1.5f variance:%1.5f iterations:%d", r_ml$estimate, 1/r_ml$hessian, r_ml$iterations))
3. MCMC(M-Hアルゴリズム)で推定してみる
さて、2節で定義した対数尤度関数を使って、M-Hアルゴリズムで推定を行ってみましょう。1万回のサンプリングを行い、Burn-in回数を500回として計算をしてみたところ、λは0.85265、分散は0.00805と推定されました。ニュートン=ラフソン法と少し値が異なりますが、概ね一致する数字のようです。
# 再現性を持たすため、乱数のシードを設定
set.seed(2658817)
# 初期値は0.1とする
s0 <- 0.1
# 初期値の尤度を求めておく。なお対数尤度関数をexp()かけている。
LL0 <- exp(-1*mlpoi(s0))
# サンプル集合sに初期値を入れる
s <- c(s0)
for(n in 1:10000){
# 正規分布でマルコフ過程を作成
s1 <- s0 + rnorm(1)
# 対数尤度関数を使うのでs1が0のときは飛ばす
if(0<s1){
# 一様分布[0,1]から乱数を出す
u <- runif(1)
# 候補値の尤度を求めておく
LL1 <- exp(-1*mlpoi(s1))
# 採用確率aを求める
a <- min(1, LL1/LL0)
# a>uならばs1、それ以外はs0を採用
if(a>u){
# s1をs0に上書き
s0 <- s1
# LL0に候補値の尤度を代入
LL0 <- LL1
}
# s0をサンプル集合sに追加
s <- c(s, s0)
}
}
# サンプルからBurn-in(最初から500)を除く
s <- tail(s, length(s)-500)
# 推定結果を表示
print(sprintf("lambda:%1.5f variance:%1.5f", mean(s), var(s)))
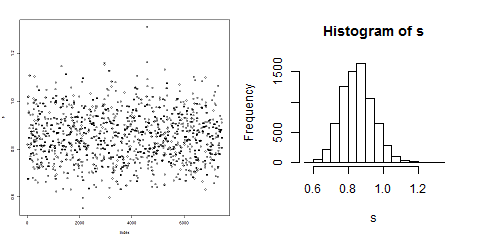
分布をプロットしてみると、MCMCを扱うパッケージのようなグラフが確認できます。
# マルコフ過程を確認
plot(s)
# 分布を確認
hist(s)
左がプロット結果、右がヒストグラムになります。分布が分かるので、95%信用区画なども求まる事が分かります。
4. おわりに
ニュートン=ラフソン法と比較するとループ回数が1428倍と圧倒的に多く、また現実的には収束点を導出する事はできないのでMCMC(M-Hアルゴリズム)はエレガントな感じはしません。それでも実用上は大きな利点が幾つもあります。
一つは、最大化する尤度関数などが与えられれば、その一階微分や二階微分無しで計算ができるのはメリットです。分布が複雑な場合でも計算ができますし、ランダムに動くので部分最適点によって計算が阻害される可能性も少ないです。また、ベイズ推定でネックになる分母の積分値の計算が不要になる事は、良く知られた利点です。
実用上は多変数でマルコフ連鎖をどう作るか、収束判定をどうするかなどの問題があるため、もっと複雑なコードが必要となりますが、以上のサンプルでM-Hアルゴリズムが基本的にシンプルな構造をしている事は理解できると思います。なお実用的に使うときは、MCMCpackなどを利用する事をお勧めします。
A. 補足
MCMC(M-Hアルゴリズム)が目的の分布に収束する理由については、「マルコフ連鎖モンテカルロ法の最近の展開」が参考になります。
B. MCMCpackの利用
上述のサンプルでMCMCpackを利用した例をあげておきます。詳細はMCMCpackの取扱説明書と「MCMCの勉強(1):Taglibro de H」を参照してください。
library(MCMCpack)
# nlm()関数とは符号を逆にし、0以下の場合は-Infを戻す
mlpoi<-function(p, x){
if(p[1] < 0.0){
return(-Inf)
}
return(sum(x*log(p[1]))-length(x)*p[1]-sum(log(factorial(x))))
}
# 引数は取扱説明書参照。なおxは1節で生成したベクトル。
post.samp <- MCMCmetrop1R(mlpoi, theta.init=c(0.1), x=x)
# トレースと分布をプロット
plot(post.samp)
# 推定結果を表示
summary(post.samp)