The identification and prediction of atrial fibrillation in coronary artery disease patients: a multicentre retrospective study based on Bayesian network.
Free full text in Europe PMC
Abstract
Background
Atrial fibrillation (AF) coexisting with coronary artery disease (CAD) remains a prevailing issue that often results in poor short- and long-term patient outcomes. Screening has been proposed as a method to increase AF detection rates and reduce the incidence of poor prognosis through early intervention. Nevertheless, due to the cost implications and uncertainty over the benefits of a systematic screening programme, the International Task Force currently recommends against screening. This study is to employ Bayesian networks (BN) for assessing the pre-test probability (PTP) of AF in patients with CAD.Methods
A total of 12,552 patients with CAD were divided into the CAD patients with AF group (CHD-AF group) and the CAD patients without AF group (non-AF group). Univariate analysis and LASSO regression method were used to screen for potential risk factors. The maximum-minimum climb (MMHC) algorithm was used to construct the directed acyclic graph (DAG) of BN. Predictive power was tested using internal validation, external validation and 10-fold internal cross-validation. Finally, the generated BN model was compared with four machine learning algorithms.Results
Fourteen indicators were included in the BN, including age, gender, systolic blood pressure (SBP), low-density lipoprotein cholesterol (LDL-C), serum uric acid (UA), gamma-glutamyltransferase (GGT), direct bilirubin (DBIL), lipoproteins [LP(a)], NYHA cardiac function grading, diabetes mellitus and hypertension, palpitation, dyspnoea and the left atrial diameter. The BN model performs well on both the test set (AUC = 0.90) and internal 10-fold cross-validation (AUC = 0.89 ± 0.01).Conclusion
The prediction model of AF with CAD constructed based on BN has high prediction performance and may provide a new tool for large-scale AF screening.Free full text
The identification and prediction of atrial fibrillation in coronary artery disease patients: a multicentre retrospective study based on Bayesian network
Abstract
Background
Atrial fibrillation (AF) coexisting with coronary artery disease (CAD) remains a prevailing issue that often results in poor short- and long-term patient outcomes. Screening has been proposed as a method to increase AF detection rates and reduce the incidence of poor prognosis through early intervention. Nevertheless, due to the cost implications and uncertainty over the benefits of a systematic screening programme, the International Task Force currently recommends against screening. This study is to employ Bayesian networks (BN) for assessing the pre-test probability (PTP) of AF in patients with CAD.
Methods
A total of 12,552 patients with CAD were divided into the CAD patients with AF group (CHD-AF group) and the CAD patients without AF group (non-AF group). Univariate analysis and LASSO regression method were used to screen for potential risk factors. The maximum-minimum climb (MMHC) algorithm was used to construct the directed acyclic graph (DAG) of BN. Predictive power was tested using internal validation, external validation and 10-fold internal cross-validation. Finally, the generated BN model was compared with four machine learning algorithms.
Results
Fourteen indicators were included in the BN, including age, gender, systolic blood pressure (SBP), low-density lipoprotein cholesterol (LDL-C), serum uric acid (UA), gamma-glutamyltransferase (GGT), direct bilirubin (DBIL), lipoproteins [LP(a)], NYHA cardiac function grading, diabetes mellitus and hypertension, palpitation, dyspnoea and the left atrial diameter. The BN model performs well on both the test set (AUC = 0.90) and internal 10-fold cross-validation (AUC = 0.89
±0.01).
Conclusion
The prediction model of AF with CAD constructed based on BN has high prediction performance and may provide a new tool for large-scale AF screening.
1. Introduction
Coronary artery disease (CAD) is the most common cardiovascular disease in clinical practice [1] and has become one of the most serious public health problems worldwide due to its high morbidity and mortality [2]. Atrial fibrillation (AF) is the most common sustained arrythmia that requires treatment, often coexisting with other cardiovascular diseases and is strongly associated with the risk of death, stroke and peripheral embolism [3]. Its prevalence is expected to more than double in the next 30years [4] and increase with age [5], especially in older adults, where the risk increases by 10% for every 5years of age [6]. However, many patients with AF are currently undetected and therefore untreated, either because they are asymptomatic or their symptoms are ignored, or because they suffer from paroxysmal AF.
CAD and AF share many of the same risk factors and frequently coexist. About one-third of patients with AF also have CAD [7], and individuals with both CAD and AF are at risk for life expectancy [8]. Meanwhile, the treatment of CAD and AF is distinct, as anticoagulants are used in AF to reduce thromboembolic events such as stroke, and antiplatelet drugs are used in CAD to reduce myocardial ischemic events [9], combining anticoagulants and antiplatelet drugs may lead to excessive bleeding and result in serious complications [10]. Therefore, the optimal treatment plan for patients diagnosed with both AF and CAD has garnered significant attention in clinical research [11]. Consequently, further examination of patients with CAD to definitively rule out or diagnose AF can assist clinicians and patients work together to develop safe prevention and treatment strategies in the early stages. Screening, such as electrocardiogram (ECG) and repeated Holter monitoring [12], has been suggested as one approach to increase AF detection rates and reduce the incidence of ischaemic stroke by earlier initiation of anticoagulation therapy [13]. However, international taskforces currently recommend against screening, citing the cost implications and uncertainty over the benefits of a systematic screening programme compared to usual care [14].
The Bayesian network (BN) underlying causal assumptions and interpretability make it a preferred choice for disease modelling [15]. Its ability to capture complex relationships between variables and estimate probabilities to improve the understanding of the disease [16, 17], particularly in elucidating the intricate web of interactions among risk factors and their contributions to disease development [18]. Therefore, this study aims to utilize Bayesian networks to establish and validate a new predictive model for predicting AF in CAD patients, in order to assess the probability of AF occurrence in CAD patients.
2. Methods
2.1. Selection and description of patients
Data were obtained from the Medical Big Data Platform of the Medical Data Research Institute of Chongqing Medical University (https://demo.yiducloud.com.cn), and patients with AF and CAD were screened from the database. Inclusion criteria: (1) data from 2013 to 2023; (2) age≥ 18years; (3) a clear history of CAD in the admission diagnosis or past history; Exclusion criteria: (1) patients with > 30% missing data; (2) previously diagnosed AF; (3) patients diagnosed with cancer, severe mental illness or suffering from other serious complications; (4) patients with severe organ failure. A total of 12,552 patients with CAD were included in four tertiary hospitals in Chongqing, namely the Second Affiliated Hospital of Chongqing Medical University, the Third Affiliated Hospital of Chongqing Medical University, the Yongchuan Hospital of Chongqing Medical University, and the University City Hospital of Chongqing Medical University. The model was also further validated by using 165 patients from the MIMIC IV (https://mimic.mit.edu/docs/iv/) database as an external validation set.
2.2. Variable selection
The diagnosis of AF followed the 2020 ESC Guidelines for the diagnosis and management of AF [19]. After excluding indicators with missing values > 30%, we collected a total of 38 indicators related to patients with AF and CAD, each patient’s demographic characteristics, as well as laboratory test results, were collected upon admission and before treatment began. All continuous data were discretized by gender, age and clinical normal reference range. The baseline characteristics and discretization process for all patients are shown in Table 1.
Table 1.
Characteristics of patients, variables and their assignments.
| Characteristic | Class | Training set | Test set | Variable description and its assignment |
|---|---|---|---|---|
| Demographic information | ||||
 AF | ||||
| Absent | 8018 (91.22%) | 3436(91.31%) | 0: Non-AF | |
| Present | 771 (8.77%) | 327 (8.69%) | 1: CHD-AF | |
| Sex | Gender | |||
| Female | 3419 (38.90%) | 1492 (39.67%) | 0: Female | |
| Male | 5370 (61.10%) | 2271 (60.33%) | 1: Male | |
| Age(year) | Age at diagnosis | |||
| Between 18–44 | 275 (3.13%) | 92 (2.45%) | 1: 18–44 | |
| Between 45–59 | 1992 (22.66%) | 875 (23.26%) | 2: 45–59 | |
| Between 60–74 | 4479 (50.96%) | 1911 (50.81%) | 3: 60–74 | |
| Between 75–89 | 2015 (22.93%) | 872 (23.17%) | 4: 75–89 | |
| Upper 90 | 28 (0.32%) | 12 (0.32%) | 5: ≥90 | |
| Smoker | Is a smoker | |||
| No | 4473 (50.89%) | 1981 (52.64%) | 0: No | |
| Yes | 4316 (49.11%) | 1782 (47.36%) | 1: Yes | |
| Drinker | History of drinking | |||
| No | 3816 (43.41%) | 1591 (42.29%) | 0: No | |
| Yes | 4973 (56.59%) | 2172 (57.71%) | 1: Yes | |
| Surgery | History of cardiac surgery | |||
| No | 2612 (29.72%) | 1128 (29.98%) | 0: Absent | |
| Yes | 6177 (70.28%) | 2635 (70.02%) | 1: Present | |
| SBP(mmHg) | Systolic blood pressure | |||
| Normal | 4949 (56.31%) | 2140 (56.87%) | Normal: ≤120 | |
| Abnormal | 3840 (43.69%) | 1623 (43.13%) | Abnormal:>120 | |
| DBP(mmHg) | Diastolic blood pressure | |||
| Normal | 6645 (75.60%) | 2861 (76.03%) | Normal: ≤80 | |
| Abnormal | 2144 (24.40%) | 902 (23.97%) | Abnormal:>80 | |
| Indications | ||||
| NYHA Classification | NYHA Classification of Heart Failure | |||
| None/Unknown | 3610 (41.07%) | 1512 (40.19%) | 0:None/Unknown | |
| I | 1959 (22.29%) | 892 (23.71%) | 1:I | |
| II | 2203 (25.07%) | 929 (24.67%) | 2:II | |
| III | 838 (9.53%) | 355 (9.44%) | 3:III | |
| IV | 179 (2.04%) | 75 (1.99%) | 4:IV | |
| Hyperlipidaemia | History of hyperlipidaemia | |||
| Absent | 6933 (78.88%) | 2939 (78.11%) | 0: Absent | |
| Present | 1856 (21.12%) | 824 (21.89%) | 1: Present | |
| Hypertension | History of hypertension | |||
| Absent | 3152 (35.86%) | 1363 (36.21%) | 0: Absent | |
| Grade 1 | 848 (9.65%) | 349 (9.28%) | 1: Grade 1 | |
| Grade 2 | 1452 (16.52%) | 617 (16.40%) | 2: Grade 2 | |
| Grade 3 | 3337 (37.97%) | 1434(38.11%) | 3: Grade 3 | |
| T2DM | Has diabetes mellitus | |||
| Absent | 5460 (62.12%) | 2361 (62.73%) | 0: Absent | |
| Present | 3329 (37.88%) | 1402 (37.27%) | 1: Present | |
| COPD | History of COPD | |||
| Absent | 8190 (93.18%) | 3512 (93.34%) | 0: Absent | |
| Present | 599 (6.82%) | 251 (6.66%) | 1: Present | |
| Chest pain | Has typical chest pain | |||
| Absent | 5412 (61.58%) | 2366 (62.88%) | 0: Absent | |
| Present | 3377 (38.42%) | 1397 (37.12%) | 1: Present | |
| Dyspnoea | Has dyspnea | |||
| Absent | 5786 (65.83%) | 2458 (65.31%) | 0: Absent | |
| Present | 3003 (34.17%) | 1305 (34.69%) | 1: Present | |
| palpitation | History of palpitation | |||
| Absent | 5615 (63.89%) | 2377 (63.16%) | 0: Absent | |
| Present | 3174 (36.11%) | 1386 (36.84%) | 1: Present | |
| CRP(mg/L) | C-reactive protein | |||
| Normal | 5887 (66.98%) | 2526 (67.13%) | Normal: <8 | |
| High | 2902 (33.02%) | 1237 (32.87%) | High: ≥8 | |
| GGT(U/L) | γ-glutamyltransferase | |||
| Normal | 6310 (71.79%) | 2682 (71.27%) | Normal: <60 | |
| High | 2479 (28.21%) | 1081 (28.73%) | High: ≥60 | |
| ALT(U/L) | Alanine aminotransferase | |||
| Normal | 7263 (82.63%) | 3113 (82.73%) | Normal: 0–40 | |
| High | 1526 (17.37%) | 650 (17.27%) | High: >40 | |
| AST(U/L) | Aspartate aminotransferase | |||
| Normal | 7246 (82.44%) | 3075 (81.73%) | Normal: 15–40 | |
| High | 1543 (17.56%) | 688 (18.27%) | High: >40 | |
| ALP(U/L) | Alkaline phosphatase | |||
| Normal | 8451 (96.14%) | 3619(96.18%) | Normal: M<125 F <135 | |
| Abnormal | 338 (3.86%) | 144 (3.82%) | Abnormal: M≥125 F ≥135 | |
| LDL-C(mmol/L) | Low-density lipoprotein cholesterol | |||
| Normal | 7210 (82.03%) | 3039 (80.75%) | Normal: <=3.12 | |
| High | 1579 (17.97%) | 724 (19.25%) | High: >3.12 | |
| HDL-C(mmol/L) | High-density lipoprotein cholesterol | |||
| Normal | 6681 (76.02%) | 2943 (78.22%) | Normal: >1 | |
| Abnormal | 2108 (23.98%) | 820 (21.78%) | Abnormal: ≤3.12 | |
| Urea(mmol/L) | Serum urea | |||
| Normal | 6541 (74.41%) | 2796 (74.32%) | Normal: 0-8 | |
| Abnormal | 2249 (25.59%) | 966 (25.68%) | High: >8 | |
| TP(g/L) | Total protein | |||
| Normal | 7591 (86.36%) | 3280 (87.17%) | Normal: 60–80 | |
| Low | 795 (9.05%) | 304 (8.07%) | Low: <60 | |
| High | 403 (4.58%) | 179 (4.76%) | High: >80 | |
| TG(mmol/L) | Triglycerides | |||
| Normal | 5631 (64.07%) | 2436 (64.74%) | Normal:≤1.7 | |
| High | 3158 (35.93%) | 1327 (35.26%) | High: >1.7 | |
| UA(μmol/L) | Serum uric acid | |||
| Normal | 6184 (70.35%) | 2661 (70.72%) | Normal: ≤428 | |
| High | 2605 (29.65%) | 1102 (29.28%) | High: >428 | |
| DBil(μmol/L) | Direct bilirubin | |||
| Normal | 8153 (92.75%) | 3484 (92.59%) | Normal: 0–8 | |
| High | 636 (7.25%) | 279 (7.41%) | High: >8 | |
| IBil(μmol/L) | Direct bilirubin | |||
| Normal | 8154 (92.76%) | 3483 (92.58%) | Normal: ≤13.68 | |
| High | 636 (7.24%) | 279 (7.42%) | High: >13.8 | |
| Crea(μmol/L) | Serum creatinine | |||
| Normal | 8272 (94.11%) | 3525 (93.70%) | Normal: M<133,F<97 | |
| High | 518 (5.89%) | 237 (6.30%) | High: M≥133,F>=97 | |
| CK-MB(ng/mL) | CK-MB | |||
| Normal | 8063 (91.73%) | 3448 (91.64%) | Normal: <5 | |
| High | 726 (8.27%) | 315 (8.36%) | High: ≥5 | |
| LP(a) (mg/L) | lipoprotein(a) | |||
| Normal | 6945 (79.01%) | 2990 (79.46%) | Normal:≤300 | |
| High | 1844 (20.99%) | 773 (20.54%) | High: >300 | |
| ALB(g/L) | Albumin | |||
| Low | 8188 (93.15%) | 3511 (93.31%) | Low: <38 | |
| Normal | 601 (6.85%) | 252 (6.69%) | Normal:≥38 | |
| NT-pro-BNP (pg/mL) | N-terminal pro-B-type natriuretic peptide | |||
| Normal | 7302 (83.07%) | 3084 (81.96%) | Normal: <450(age < 50)<900(50≤age ≤5)≥1800(age > 75) | |
| High | 1487 (16.93%) | 679 (18.04%) | High: ≥450(age < 50)≥900(50≤age ≤ 75)≥1800(age >75) | |
| Echocardiography | ||||
| LVEF(%) | ||||
| Normal | 8139 (92.60%) | 3486 (92.65%) | Normal:>50% | |
| Reduced | 650 (7.40%) | 277 (7.35%) | Reduced:≥50% | |
| LAD(mm) | ||||
| Normal | 4301 (48.94%) | 1899 (50.45%) | Normal:<35 | |
| Enlarged | 4488 (51.06%) | 1864 (49.55%) | Enlarged ≥ 35 | |
| IVST(mm) | Interventricular septal thickness | |||
| Normal | 6305 (71.74%) | 2755 (73.21%) | Normal:<12 | |
| Increased | 2484 (28.26%) | 1008 (26.79%) | Increased:≥12 | |
| LVEDD(mm) | left ventricular end-diastolic diameter | |||
| Decreased | 1336 (15.20%) | 572 (15.20%) | Decreased:M:<45,F<35 | |
| Normal | 6601 (75.11%) | 2843 (75.54%) | Normal:M:45–55, F:35–50 | |
| Increased | 852 (9.69%) | 348 (9.25%) | Increased: M>55, F>50 | |
| FS(%) | Fraction Shorting | |||
| Decreased | 1157 (13.16%) | 491 (13.05%) | Decreased:<25 | |
| Normal | 6826 (77.67%) | 2955 (78.52%) | Normal:25–45 | |
| Increased | 806 (9.17%) | 317 (8.43%) | Increased:>45 | |
2.3. Bayesian network
BN is a compact and intuitive graphical representation of joint probability distributions (JPD) that can be used for causal inference and risk prediction analysis [20], and many scholars have developed relevant disease risk assessment and diagnosis prediction models based on BN and achieved good prediction results in clinical applications. BN consists of a directed acyclic graph G= (V, E) and a set of conditional probability distributions P. The directed acyclic graph G= (V, E) consists of nodes and directed edges between nodes, with the nodes representing random variables and directed arcs representing probability dependencies between variables Xi and Xj. If there is a directed edge from Xi to Xj, we call Xj the parent node of Xi, and Xi the sub-node of Xj, and the conditional probability distribution P represents the conditional probability distribution of each node Xi in a given parent. The directed acyclic graph G qualitatively portrays the dependence and independence between variables, while the conditional probability distribution quantitatively describes the degree of probabilistic dependence of a node on its parent node. When the probability distribution of a node’s parent is determined, the node is conditionally independent of all its non-direct parent nodes. The factorization of BN’ global distribution is specified as [21]:
Usually, BN is constructed in three ways: (1) Fully through the empirical knowledge of experts, which is a very tedious process, especially when the model contains a large number of parameters, and therefore is mainly used when there is no available data [22]; (2) Purely automated or machine learning, which emphasizes the use of conditional dependencies in data to derive model structure. In an algorithmic perspective, the construction of a BN consists of two steps: structure learning and parameter learning. Structure learning includes constraint-based algorithm, and fraction-based algorithm, due to the limitations of these two algorithms, some scholars proposed a hybrid algorithm based on the above two, namely the Max–Min Hill Climbing algorithm (MMHC), which overcomes the disadvantages of constraint-based and fraction-based search algorithms [23]. Parameter learning can be traced back to the great likelihood estimation and Bayesian estimation [21]. And (3) Combining expert experience and database learning to establish the network structure and determine the conditional probability values. This study adopts the 3rd way of learning, in which the expert experience is mainly based on literature summarization and systematic review: in the preliminary stage of the study, based on the theory of evidence-based medicine, we systematically searched domestic and international relevant literature on CAD patients with comorbid AF [11, 13, 24, 25] and carried out a systematic review and analysis; in combination with the above a priori theory, we manually adjusted the constructed BN and used the Netica software to carry out BN inference.
2.4. Procedural information and statistics
Statistical analysis was performed using R software (version 4.2.1), and missing indicators were imputed in using the predictive mean matching (PMM) method algorithm in the ‘mice’ package in R. BN model construction was performed using Python, and the count data were expressed as n (%), and the χ2 test was used for comparison between groups, p<0.05 was considered a statistically significant. We evaluated the model performance using the 10-fold cross-validation method and the internal and external validation sets, respectively. We assessed the predictive ability of the model using the area under the ROC curve (AUC), which was generated by plotting sensitivity and 1-specificity. We also evaluated the calibration of the model by plotting calibration curves, which are used to measure the degree to which the probability of the model output corresponds to the observed disease risk. Decision curve analysis was used to determine the clinical practicability.
3. Results
3.1. Patient characteristics
A total of 12,552 patients with CAD were included in this study, and their clinicopathological features were summarized in Table 1. A total of 1098 (9.6%) were diagnosed with AF. Moreover, 165 patients from MIMIC database were enrolled as the external validation cohort. To ensure the accuracy of the model prediction performance, a random under-sampling (RUS) was used to obtain the ratio of 1:2 positive to negative in the training set (Figure S1).
3.2. Univariate and LASSO regression analyses
A total of 38 indicators were included in the univariate analysis, including 15 baseline indicators and 23 laboratory test indicators. The results of the univariate analysis showed that there were statistically significant differences in 27 indicators between the two groups (p<0.05) (Table 2). LASSO regression analysis of the risk factors with statistical significance found in the above univariate analysis was performed, the results of which are shown in Figure 1. Although there were no statistically significant difference in DM and hypertension between the two groups in this study, we reviewed previous studies and consensus from other scholars and found that diabetes and hypertension are remarkable factors among the many influencing factors of CAD and AF and play a very significant role in the process of CAD combined with AF. Therefore, in this study, we included diabetes and hypertension as influential factor in the subsequent model construction. Finally, these clinical predictive features were included in a BN for further analysis.
Risk factors selection using the lasso regression method.
Table 2.
Univariate analysis of related factors in CAD group and CAD-AF group.
| Variables | CAD Group (n =8018) | CAD-AF Group (n =771) | OR (95%CI) | P |
|---|---|---|---|---|
| Sex, n(%) | ||||
| Male | 4961 (61.87) | 409 (53.05) | 1.00 (Reference) | |
| Female | 3057 (38.13) | 362 (46.95) | 1.44 (1.24~1.67) | <0.001 |
| Age, n(%) | ||||
| Between 18–44 | 268 (3.34) | 7 (0.91) | 1.00 (Reference) | |
| Between 45–59 | 1913 (23.86) | 79 (10.25) | 1.58 (0.72~3.46) | 0.252 |
| Between 60–74 | 4101 (51.15) | 378 (49.03) | 3.53 (1.65~7.53) | 0.001 |
| Between 75–89 | 1713 (21.36) | 302 (39.17) | 6.75 (3.16~14.44) | <0.001 |
| Upper 90 | 23 (0.29) | 5 (0.65) | 8.32 (2.45~28.31) | <0.001 |
| Surgery, n(%) | ||||
| No | 3892 (48.54) | 424 (54.99) | 1.00 (Reference) | |
| Yes | 4126 (51.46) | 347 (45.01) | 0.77 (0.67~0.90) | <0.001 |
| Smoker, n(%) | ||||
| No | 3532 (44.05) | 283 (36.71) | 1.00 (Reference) | |
| Yes | 4486 (55.95) | 488 (63.29) | 1.36 (1.17~1.58) | <0.001 |
| Drinker, n(%) | ||||
| No | 2395 (29.87) | 216 (28.02) | 1.00 (Reference) | |
| Yes | 5623 (70.13) | 555 (71.98) | 1.09 (0.93~1.29) | 0.282 |
| SBP, n(%) | ||||
| Normal | 4475 (55.81) | 474 (61.48) | 1.00 (Reference) | |
| Abnormal | 3543 (44.19) | 297 (38.52) | 0.79 (0.68~0.92) | 0.002 |
| DBP, n(%) | ||||
| Normal | 6067 (75.67) | 578 (74.97) | 1.00 (Reference) | |
| Abnormal | 1951 (24.33) | 193 (25.03) | 1.04 (0.88~1.23) | 0.666 |
| IBIL, n(%) | ||||
| Normal | 7365 (91.86) | 699 (90.66) | 1.00 (Reference) | |
| Abnormal | 653 (8.14) | 72 (9.34) | 1.16 (0.90~1.50) | 0.250 |
| LDL-C, n(%) | ||||
| Normal | 6526 (81.39) | 684 (88.72) | 1.00 (Reference) | |
| Abnormal | 1492 (18.61) | 87 (11.28) | 0.56 (0.44~0.70) | <0.001 |
| UA, n(%) | ||||
| Normal | 5753 (71.75) | 431 (55.90) | 1.00 (Reference) | |
| Abnormal | 2265 (28.25) | 340 (44.10) | 2.00 (1.72~2.33) | <0.001 |
| AST, n(%) | ||||
| Normal | 6614 (82.49) | 631 (81.84) | 1.00 (Reference) | |
| Abnormal | 1404 (17.51) | 140 (18.16) | 1.05 (0.86~1.27) | 0.652 |
| Urea, n(%) | ||||
| Normal | 6051 (75.47) | 489 (63.42) | 1.00 (Reference) | |
| Abnormal | 1967 (24.53) | 282 (36.58) | 1.77 (1.52~2.07) | <.001 |
| TG, n(%) | ||||
| Normal | 5094 (63.53) | 536 (69.52) | 1.00 (Reference) | |
| Abnormal | 2924 (36.47) | 235 (30.48) | 0.76 (0.65~0.90) | <.001 |
| ALT, n(%) | ||||
| Normal | 6632 (82.71) | 631 (81.84) | 1.00 (Reference) | |
| Abnormal | 1386 (17.29) | 140 (18.16) | 1.06 (0.88~1.29) | 0.541 |
| CK MB, n(%) | ||||
| Normal | 7342 (91.57) | 721 (93.51) | 1.00 (Reference) | |
| Abnormal | 676 (8.43) | 50 (6.49) | 0.75 (0.56~1.01) | 0.062 |
| ALB, n(%) | ||||
| Normal | 7488 (93.39) | 700 (90.79) | 1.00 (Reference) | |
| Abnormal | 530 (6.61) | 71 (9.21) | 1.43 (1.11~1.86) | 0.007 |
| TP, n(%) | ||||
| Low | 700 (8.73) | 95 (12.32) | 1.00 (Reference) | |
| Normal | 6943 (86.59) | 648 (84.05) | 0.69 (0.55~0.86) | 0.001 |
| High | 375 (4.68) | 28 (3.63) | 0.55 (0.35~0.85) | 0.008 |
| GGT, n(%) | ||||
| Normal | 5832 (72.74) | 478 (62.00) | 1.00 (Reference) | |
| High | 2186 (27.26) | 293 (38.00) | 1.64 (1.40~1.91) | <0.001 |
| ALP, n(%) | ||||
| Normal | 7709 (96.15) | 742 (96.24) | 1.00 (Reference) | |
| Abnormal | 309 (3.85) | 29 (3.76) | 0.98 (0.66~1.44) | 0.899 |
| Crea, n(%) | ||||
| Normal | 7588 (94.64) | 683 (88.59) | 1.00 (Reference) | |
| Abnormal | 430 (5.36) | 88 (11.41) | 2.27 (1.78~2.90) | <0.001 |
| DBIL, n(%) | ||||
| Normal | 7480 (93.29) | 673 (87.29) | 1.00 (Reference) | |
| Abnormal | 538 (6.71) | 98 (12.71) | 2.02 (1.61~2.55) | <0.001 |
| HDL C, n(%) | ||||
| Normal | 6078 (75.80) | 602 (78.08) | 1.00 (Reference) | |
| Abnormal | 1940 (24.20) | 169 (21.92) | 0.88 (0.74~1.05) | 0.158 |
| CRP, n(%) | ||||
| Normal | 5426 (67.67) | 461 (59.79) | 1.00 (Reference) | |
| Abnormal | 2592 (32.33) | 310 (40.21) | 1.41 (1.21~1.64) | <0.001 |
| LP (a) n(%) | ||||
| Normal | 6461 (80.58) | 484 (62.78) | 1.00 (Reference) | |
| Abnormal | 1557 (19.42) | 287 (37.22) | 2.46 (2.10~2.88) | <0.001 |
| NT pro BNP, n(%) | ||||
| Normal | 6643 (82.85) | 659 (85.47) | 1.00 (Reference) | |
| Abnormal | 1375 (17.15) | 112 (14.53) | 0.82 (0.67~1.01) | 0.064 |
| NYHA, n(%) | ||||
| Non/UNK | 3428 (42.75) | 182 (23.61) | 1.00 (Reference) | |
| I | 1848 (23.05) | 111 (14.40) | 1.13 (0.89~1.44) | 0.319 |
| II | 2015 (25.13) | 188 (24.38) | 1.76 (1.42~2.17) | <0.001 |
| III | 646 (8.06) | 192 (24.90) | 5.60 (4.49~6.97) | <0.001 |
| IV | 81 (1.01) | 98 (12.71) | 22.79 (16.38~31.70) | <0.001 |
| DM, n(%) | ||||
| Absent | 5000 (62.36) | 460 (59.66) | 1.00 (Reference) | |
| Present | 3018 (37.64) | 311 (40.34) | 1.12 (0.96~1.30) | 0.141 |
| HBP, n(%) | ||||
| Absent | 2895 (36.11) | 257 (33.33) | 1.00 (Reference) | |
| Grade 1 | 812 (10.13) | 36 (4.67) | 0.50 (0.35~0.71) | <0.001 |
| Grade 2 | 1303 (16.25) | 149 (19.33) | 1.29 (1.04~1.59) | 0.019 |
| Grade 3 | 3008 (37.52) | 329 (42.67) | 1.23 (1.04~1.46) | 0.017 |
| COPD, n(%) | ||||
| Absent | 7487 (93.38) | 703 (91.18) | 1.00 (Reference) | |
| Present | 531 (6.62) | 68 (8.82) | 1.36 (1.05~1.78) | 0.021 |
| HL, n(%) | ||||
| Absent | 6333 (78.98) | 599 (77.69) | 1.00 (Reference) | |
| Present | 1685 (21.02) | 172 (22.31) | 1.08 (0.90~1.29) | 0.401 |
| Palpitation, n(%) | ||||
| Absent | 5334 (66.53) | 281 (36.45) | 1.00 (Reference) | |
| Present | 2684 (33.47) | 490 (63.55) | 3.47 (2.97~4.04) | <0.001 |
| Dyspnoea, n(%) | ||||
| Absent | 5533 (69.01) | 253 (32.81) | 1.00 (Reference) | |
| Present | 2485 (30.99) | 518 (67.19) | 4.56 (3.89~5.34) | <0.001 |
| Chest pain, n(%) | ||||
| Absent | 4898 (61.09) | 513 (66.54) | 1.00 (Reference) | |
| Present | 3120 (38.91) | 258 (33.46) | 0.79 (0.68~0.92) | 0.003 |
| LVEF(%), n(%) | ||||
| Normal | 7493 (93.45) | 646 (83.79) | 1.00 (Reference) | |
| Reduced | 525 (6.55) | 125 (16.21) | 2.76 (2.24~3.41) | <0.001 |
| LAD, n(%) | ||||
| Normal | 4269 (53.24) | 32 (4.15) | 1.00 (Reference) | |
| Enlarged | 3749 (46.76) | 739 (95.85) | 26.30 (18.41~37.56) | <0.001 |
| IVST, n(%) | ||||
| Normal | 5791 (72.22) | 515 (66.80) | 1.00 (Reference) | |
| Increased | 2227 (27.78) | 256 (33.20) | 1.29 (1.10~1.51) | 0.001 |
| LVP, n(%) | ||||
| Decreased | 1240 (15.47) | 96 (12.45) | 1.00 (Reference) | |
| Normal | 6078 (75.80) | 523 (67.83) | 1.11 (0.89~1.39) | 0.360 |
| Increased | 700 (8.73) | 152 (19.71) | 2.80 (2.14~3.68) | <0.001 |
| FS, n(%) | ||||
| Decreased | 973 (12.14) | 184 (23.87) | 1.00 (Reference) | |
| Normal | 6301 (78.59) | 526 (68.22) | 0.44 (0.37~0.53) | <0.001 |
| Increased | 744 (9.28) | 61 (7.91) | 0.43 (0.32~0.59) | <0.001 |
Statistically significant level of less than 0.05 results are indicated with bold text in the p value column.
3.3. Development and validation of BN
The BN constructed based on the MMHC algorithm and adjusted to incorporate expert knowledge is shown in Figure 2. Netica software (version 5.18) was used to visualize the model. We included the above statistically significant correlated variables in the BN model, and all probability distributions are shown in the nodes, each node representing a variable and the arcs connecting the nodes indicate probabilistic dependencies.
BN constructed based on MMHC algorithm and manual adjustment.
In the CAD-AF model, there are 15 nodes and 23 directed edges between CAD-AF and its predictors. Figure 2 shows the complex network structure of the CAD-AF model, where Age, LDL-C, uric acid (UA), NYHA Classification, LP(a), LAD and diabetes mellitus are observed as parent nodes of the CAD-AF. Dyspnoea and palpitation were associated with CAD-AF as child nodes. And other variables were indirectly associated with CAD-AF by affecting the direct effect variables with CAD-AF. Moreover, the diagnostic reasoning process unfolds in Figure 3, elucidating how BN methodically infers AF likelihood within CAD context.
The diagnostic and inference prediction process of BN.
Step 1: Initial Assessment (Figure 3(a)): (1) Patient Profile: 65-year-old male with CAD, presenting with palpitations. (2) Medical History: Diabetes Mellitus (Present), Hypertension (Absent), NYHA III. Initial AF Risk (Figure 3(a)): BN predicts 11.6%.
Step 2: Further Testing (Figure 3(b)): (1)Laboratory Results: LDL-C, GGT, DBIL (normal); LP(a), UA (abnormal). (2) Cardiac Ultrasound: Enlarged left atrial diameter. Updated AF Risk (Figure 3b): BN revises to 87.4%.
3.4. Evaluation of the BN’s predictive capability
As shown in Figure 4(a,b), the AUC is 0.87 and 0.85 (95%CI: 0.84–0.86) for the test set and internal 10-fold cross-validation, respectively, which shows that the model has a high prediction accuracy. The calibration curve showed that the BN model fitted well (Figure 5(a)), and the decision curve analysis showed the clinical usefulness of the BN model (Figure 5(b)).
ROC analysis of BN on test set(a) and internal 10-fold cross-validation(b).
The calibration curves and decision curve analysis of the BN in the test set.
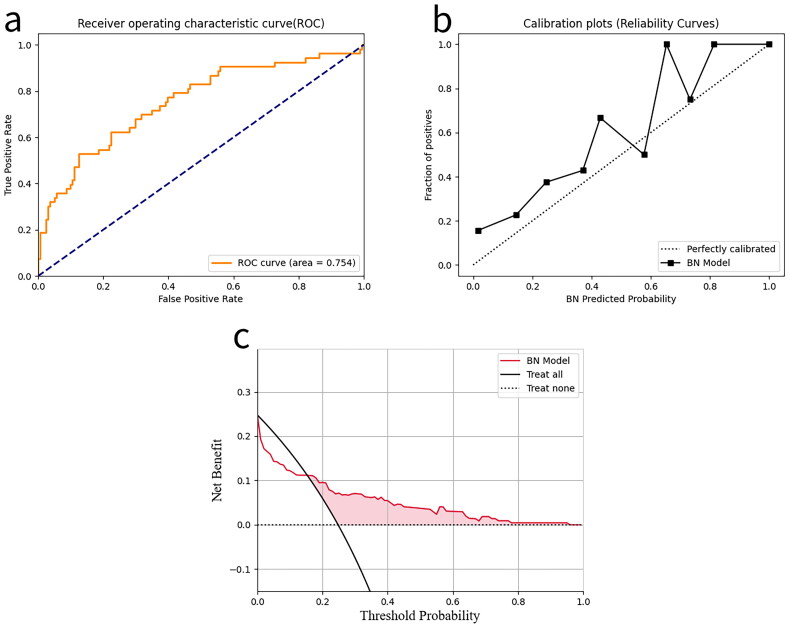
We also externally validated the constructed BN using 165 patients from the MIMIC database. However, due to the large amount of missing LP(a) data for such patients in the MIMIC database, taking advantage of the flexibility of the BN to be simplified (or expanded), this node and the associated edges were temporarily excluded from the network during external validation. As can be seen from the Figure 6(a), the model still exhibits good predictive performance (AUC = 0.754), although there is a substantial decrease in the performance of the external validation set compared to the results of the previous test set. Figure 6(b) shows the calibration curve of our model in the external validation, this curve deviates somewhat from the actual true probability, and this deviation indicates that the model’s predicted probabilities are not completely accurate. Figure 6(c) shows the decision curve of our model in external validation, the decision-making strategy based on the BN model outperforms the other two strategies over a wide range and maintains a certain net gain even when the threshold is high.
External validation based on MIMIC database BN.
Meanwhile, we compared the constructed BN with four machine learning algorithms, namely, logistic regression(LR), random forest(RF), XGBoost and LightGBM (Figure S2). The results show that the BN model is comparable or better than LR, RF, XGBoost and LightGBM (AUC values of 0.889, 0.871, 0.882 and 0.898, respectively).
4. Discussion
In this retrospective study, we analysed the clinical data of 12,552 patients with CAD and constructed a BN model. The model can provide an individualized risk assessment that could help in making decisions about treatment options such as subsequent treatment planning and follow-up strategies and thus reduce the occurrence of fatal cardiovascular events. More specifically, the model can help patients with CAD decide whether to pursue early prevention or identification of AF or support shared decision-making between clinicians and patients to decide on further treatment at low cost and low risk.
Fourteen risk factors for CAD combined with AF were screened in this study, including age,Sex, SBP, hypertension history, diabetes history, LDL-C, UA, GGT, DBIL, LP(a) and NYHA classification, LAD, as well as patients’ chief complaints including palpitation and dyspnoea. Among the variables we selected, age, sex, SBP, hypertension history, diabetes history are key risk factors for CAD and AF, which is consistent with the existing literature [4, 13, 26–32]. GGT and DBil are markers of liver function with less reported mechanisms of action in the cardiovascular field, but have also received attention in recent years for their potential roles in CAD and AF. In patients with CAD, there is an independent correlation between elevated GGT activity and AF, suggesting that it may serve as a circulating marker of AF risk [33]. Similarly, DBil has been associated with the risk of coronary atherosclerosis [34], but the exact mechanism needs to be further investigated.
Studies have shown that serum uric acid is significantly associated with the risk of CAD and AF, and patients with CAD are more likely to develop AF when UA levels are high [35]. Our study also incorporated NYHA classification, a widely used measure of heart failure (HF) severity. It has been suggested that AF may exacerbate HF, and similarly, HF may be a trigger for AF. Although it is not possible to determine the exact sequence of events, the reality is that AF can lead to worsening of the heart’s pumping function, and patients with HF are likely to develop AF over time. Notably, even those patients whose initial diagnosis is only AF may have an underlying occult cardiomyopathy that triggers AF [36]. Therefore, accurate identification and classification of HF is particularly important in the individualized management of patients with AF. Lipoprotein(a) and LDL-C are strongly associated with the development of cardiovascular disease. It has been suggested that Lp(a) levels are an independent risk factor for the development of AF in patients with CAD [37, 38]. Also, in the progression of AF, LDL-C has been shown to be an independent risk factor for thromboembolic events in AF [39–41]. Evidence from many studies in recent years suggests that enlargement of the left atrium is an important risk factor for the development of atrial fibrillation [42]. Some scholars have argued that left atrial dilatation is a high-risk indicator of AF through multicentre data analysis in the Framingham study. Their multicentre data showed that for every 5-mm increase in left atrial internal diameter, the Hazard Ratio (HR) for the occurrence of AF increased by approximately 1.39 times [43]. Similarly, it has been noted that LA diameter is significantly larger in patients with CAD combined with AF than in non-AF patients and correlates with the prevalence of AF in CAD. The two main causes of left atrial dilatation are pressure overload and volume overload, respectively. Sustained increases in left atrial pressure significantly increase the risk of structural deformation of the left atrium and may induce AF [44].
The common symptoms of patients with AF are dyspnoea, palpitations, and these symptoms overlap with those in patients with CAD [12, 45]. Therefore, patients can easily confuse these two diseases, which may also lead to delays in treatment. Therefore, the inclusion of common and easily overlooked symptoms of AF in our study will contribute to improve the public’s ability to recognize the early symptoms of AF and promote early diagnosis, thus reducing the serious consequences of failure to detect AF in time.
In the era of precision medicine, clinicians are increasingly interested in the use of predictive models to guide prevention and treatment planning [46]. The use of computer technology for disease prediction and diagnosis has been studied more frequently, providing research ideas and methods for this study. However, there are inevitably certain limitations: (1) model construction relies only on the data, ignoring the accepted clinical consensus and existing a priori knowledge; (2) the constructed models are not highly flexible and cannot respond quickly to new situations and new knowledge that may arise at any time in the clinical setting. (3) The patients’ chief complaints were not included in the modelling. One thing we have to acknowledge is that the patient’s own health information is the first source of information for clinicians, and this should be noted in clinical work. our study selected a specific group of patients with CAD and chose a flexible BN for modelling based on the basic characteristics of patients, laboratory test indexes and patients’ chief complaints, combined with the existing clinical consensus, which solved the above shortcomings to some extent.
The current study has some limitations: (1)Due to the retrospective nature of this study, there are missing values and the use of techniques to estimate the missing data may be somewhat biased. (2)The indicators with missing values >30% (e.g. BMI) were not included in this study, which may have some impact on the accuracy of the model. (3) In the actual treatment, some AF patients did not complete all the necessary tests, or their test results showed false-negative, which means that there may be a bias in the data on which our model is based for prediction, which may lead to underestimation of the prediction results to a certain extent. (4) The severity of CAD is an important cause of AF, and the future studies should consider incorporating SYNTAX scores or other validated measures of CAD severity to refine prediction models. One of the advantages of BNs, however, is that they can be updated with new evidence, allowing them to be updated by using information about new candidate biomarkers, which will be taken into account in our subsequent studies.
5. Conclusion
In summary, this study determined risk factors for AF in patients with CAD and the interactions between those risk factors and developed a BN model for personalized clinical decision making between clinicians and patients. Moreover, the internal and external validation cohort results demonstrated that the BN performed well and had high accuracy and reliability. We believe that the BN model constructed in this study could guide follow-up management strategies for patients with AF and help clinicians improve individual treatment, as well as might offer a way to cost-effectively screen for AF in a primary care setting. Meanwhile, a larger sample and multicentre study is required to validate and improve our study in the future.
Acknowledgements
All authors thank their respective institutions for their support. We are also thankful to the Intelligent Medicine Research Project of Chongqing Medical University (YJSZHYX202212) and Chongqing Municipal Science and Technology Bureau Project (cstc2018jscx-msybx0123) for funding this study.
Contributorship
JJ analyzed and interpreted the patient data regarding the coronary artery disease and atrial fibrillation; Conceptualization, JJ., CJ and LQ.Z.; methodology, ST.H.; software, YZ.; validation, BL., XL.X.; formal analysis, WJ.W.; resources, MX.X.; data curation, TT.W.; writing—original draft preparation, JJ. LQ.Z.; writing—review and editing, WJ. W. BL. XL.X.; supervision, XL.X.; project administration, BL. XL.X. All authors reviewed and edited the manuscript and approved the final version of the manuscript.
Ethical approval
The present study complied with the Declaration of Helsinki principles and was approved by the Ethics Committee of Chongqing Medical University (reference number 2023004). Due to the retrospective study design and the thorough anonymization and deidentification of patient data conducted prior to analysis, the need for obtaining patient consent was deemed unnecessary and therefore waived.
Availability of data and materials
The datasets for this study can be found in Medical Big Data Platform of the Medical Data Research Institute of Chongqing Medical University (https://demo.yiducloud.com.cn) and MIMIC IV (https://mimic.mit.edu/docs/iv/) databases.
References
Articles from Annals of Medicine are provided here courtesy of Taylor & Francis
Full text links
Read article at publisher's site: https://doi.org/10.1080/07853890.2024.2423789
Similar Articles
To arrive at the top five similar articles we use a word-weighted algorithm to compare words from the Title and Abstract of each citation.
A dynamic nomogram for predicting in-hospital major adverse cardiovascular and cerebrovascular events in patients with both coronary artery disease and atrial fibrillation: a multicenter retrospective study.
Coron Artery Dis, 35(8):659-667, 06 Jun 2024
Cited by: 0 articles | PMID: 38836650
Identification of potential biomarkers for atrial fibrillation and stable coronary artery disease based on WGCNA and machine algorithms.
BMC Cardiovasc Disord, 24(1):401, 02 Aug 2024
Cited by: 0 articles | PMID: 39090590 | PMCID: PMC11295489
Impact of coronary artery disease and revascularization on recurrence of atrial fibrillation after catheter ablation: Importance of ischemia in managing atrial fibrillation.
J Cardiovasc Electrophysiol, 30(9):1491-1498, 25 Jun 2019
Cited by: 16 articles | PMID: 31190437
Patients with atrial fibrillation and coronary artery disease - Double trouble.
Adv Med Sci, 63(1):30-35, 14 Aug 2017
Cited by: 81 articles | PMID: 28818746
Review
Funding
Funders who supported this work.
Chongqing Science and Technology Bureau (1)
Grant ID: cstc2018jscx-msybx0123
the Intelligent Medicine Research Project of Chongqing Medical University (1)
Grant ID: YJSZHYX202212
