ゲームの世界の経済学が現実世界に通用するという話

最近、私の会社では年商1,000億円ぐらいの規模の会社の販売管理系のシステムを開発しているのだが、どうもこのシステムの設計意図が私にとってはまさにデジャヴというか、「もうかれこれ10年ぐらい前にこれと同じこと考えてたよなー」と思ったので、そのあたりのことをだらだらと書いてみる。

いま、話を単純化するために店頭販売価格をいくらにすればいいかを決定するシステムを作りたいとしよう。

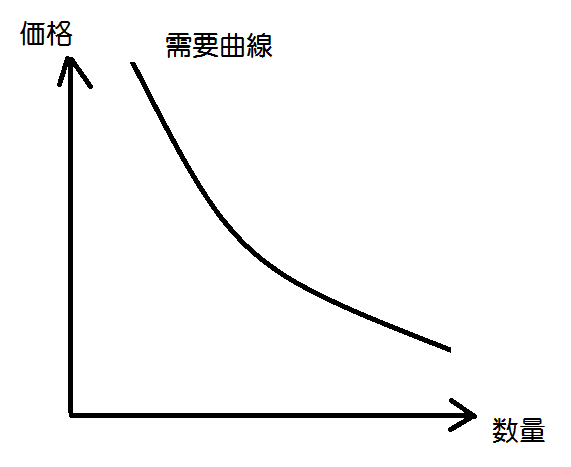
まず、経済学の教科書によく載っている需要曲線というのは次図のような反比例っぽいグラフである。

経済学の教科書では、これと供給曲線とを重ね合わせて、その交点が均衡価格(市場価格)だと説明がある。

販売する側の視点に立った場合、最適な価格(利益を最大化できる価格)というのは、均衡価格では決してない。そこで、いま供給曲線については考えないことにして、利益を最大化できる価格で売る、とだけ考えよう。

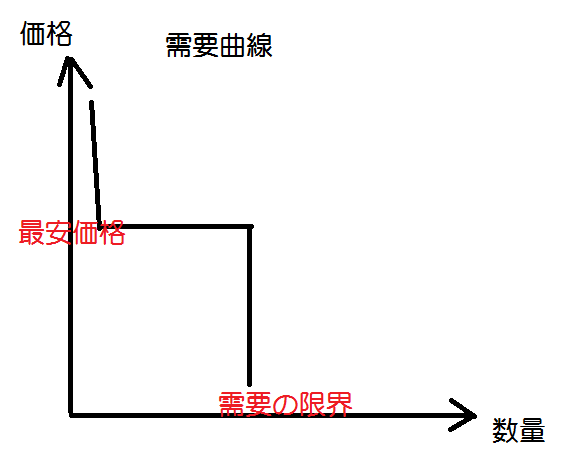
近年、インターネットの価格比較サイト等の発展により、インターネット上で最安価格を見つけることが容易となった。それゆえ、需要曲線は上記のような反比例っぽいグラフにならない。典型的には次のようなグラフになる。(ただし経済学ではこれは需要曲線とは呼ばないようなので、以下で「需要曲線」と書いてあるのは「価格に対して実際に売れる量の曲線」とでも読み替えて欲しい。)

最安価格でなければほとんど売れない。ほとんど売れないながらも、ゼロではない。それは例えば、店頭販売であれば、わざわざ他の店を回るコストを考えるとそこで買ったほうがいいというような判断もあるだろうし、そのお客さんはその店のことがお気に入りなのかも知れない。あるいは、他の店のほうが安いことを知らないのかも知れない。

この傾向はインターネットでも同様であり、同じ店で買ったほうがまとめて発送できて送料が安くなるからだとか、ちょっとぐらいの差なら信頼できるほうの店で買うだとか、比較サイトで比較するのが面倒なのでいつも買っているところでいいやだとか、まあ、そういう人たちが一定数は存在して、最安価格からある程度離れていてもそこで買うのである。

また、需要は無限にあるわけではなく(いくら安くとも要らないものは要らない)、値段をかなり下げたところで一定数以上は売れないという需要の限界値がある。

上図のような需要曲線になるとき、販売者側に立って、利益を最大化する価格とはどこかというのをいま問題として考える。

ここで前提条件をさらに追加しておかなければならないのだが、正確な需要の限界値は、売り手は事前にはわからないということである。「おおよそ100ぐらいだろう」だとか、予測を立てることは出来るが、正確な数字ではない。販売できなくて在庫が余るリスクを考えれば、資金効率を考えるなら、確実に売れるとわかっている程度の数だけ仕入れたほうが効率が良い。(価格を少し下げれば、売りきることができるタイプの商品であれば、このようなリスクをあまり考えなくて良く、一括仕入れによる値引きがあるなら、多めに仕入れることにも合理性があるのだが、私がいまここで取り扱おうとしている商品は、そういうタイプの商品ではないとする。)

このとき、需要の限界値の半数ぐらいしか仕入れていないので、多少売れ残った場合でも最安価格にすれば在庫を処分することができる。最安価格がそれほど変動しないなら、利益を最大化できる販売価格というのは、最安価格では決してないことがわかる。

例えば、次のような売り方に合理性がある。

50個仕入れたとして、一気に50個が売れるわけではない。だから、10個と40個に分け、別の店舗にて、前者は最安価格よりかなり高めで売り、後者は最安価格で売る。

前者を「かなり高め」に設定するのは、「最安価格より少し高め」と「最安価格よりかなり高め」とどちらのケースでも販売できる個数に大差がないため(上図のグラフを見ればそれが如実にわかる)、それならばかなり高めにしたほうが利益を最大化できるからである。

前者が売れ残ったら、後者の店舗で売る。前者が売り切れたら後者の店舗から在庫を補充する。このように、店舗ごとにそれぞれ異なる価格で販売することで売り手が利益を拡大出来る。

これが店頭販売価格をインターネット上の最安価格よりかなり高めに設定し、ネット販売の価格をインターネットでの最安価格に設定するという価格設定を行なうことで利益の拡大ができるということに対する合理的な説明である。(最近、家電量販店でそういう価格のつけかたをしているところがよくある。)

私がこの仕組みに気づいたのは10年ほど前にオンラインゲームをやっていたときである。そのときに売り手(販売商人)として利益を最大化するためにこの手の統計をとっていたときに需給曲線が上図のようないびつな形であることに気づいた。

そこで、そのオンラインゲームでは私は複数アカウントを用いて、同じアイテムに対してそれぞれに違う価格をつけて販売していた。これはそこそこうまくいった試みだった。

しかし、そのオンラインゲームにはゲーム内オークションのような仕組みはなく、単に露店売り(マップ上に直接露店を出すタイプ)であったために、露店ひとつひとつをクリックせねば販売商品を確認できなかった。それゆえ、最安の露店を探す手間が馬鹿にならず、面倒くさいので少しぐらい高くとも買っていく人が一定数存在した。

つまり、ゲームの世界は上のような極端な需要曲線にはなっていなかったし、そのとき、私は「ゲームの世界(非現実世界)と言えども、どこか現実味があるな」と思った。

ところが、インターネット販売では近年比較サイトの興隆により、最低価格より少しでも高いと途端に売れなくなるという、ある意味ゲームの世界以上に極限化された世界となった。あのとき私が体験したゲームの世界より、さらに非現実的な世界、それが現実の世界として眼前に広がっているのだ。

それゆえ、私が10年も前に考えたオンラインゲーム内のアイテムの販売価格の決定のための仕組みが、現代において、年商1,000億円規模の会社で通用するというわけだ。イギリスの詩人バイロンは「事実は小説よりも奇なり」と言ったが、私に言わせれば「(インターネットを含めた)現実の世界はゲームの世界よりゲームの世界なり」である。