
Empire (H. Beam Piper book)
Empire is a collection of short stories written by H. Beam Piper, and edited by John F. Carr. The book was published in 1981 by Ace Books, and again in 1986. Most of these stories take place in his Terro-Human Future History, with the sole exception being "The Return".
Contents
A short, 35-entry timeline of Piper’s Terro-Human Future History, covering from 1 A.E. to 2936 A.E.
First appeared in Amazing Stories, May 1957.
First appeared in ‘’Analog’’, April 1962.
First appeared in ‘’Astounding Science Fiction’’, December 1958.
First appeared in ‘’Astounding Science Fiction’’, January 1954.
First appeared in ‘’Venture Science Fiction’’, July 1957.
References

Shadow Complex
Shadow Complex is a 2009 platform-adventure video game developed by Chair Entertainment in association with Epic Games (using its Unreal Engine 3) and published by Microsoft Game Studios for the Xbox 360 through Xbox Live Arcade. The game was released worldwide on August 19, 2009. The original script of Shadow Complex was written by comic book writer and Star Trek novelist Peter David.
The game follows Jason Flemming and his new girlfriend Claire, who opts to explore some caverns the two stumble across. When she does not respond to his calls, Jason follows her. He finds a massive underground complex with soldiers and high-end technology. Jason must rescue Claire and discover the plot behind the faction operating the complex.
Shadow Complex's reception has been very positive. It has received and been nominated for several Game of the Year and Editor's Choice Awards. Critics praised the gameplay, narrative and graphics, with several reviewers also stating that its 1200 Microsoft Points price was a bargain. It also broke all sales records for Xbox Live Arcade titles, selling over 200,000 units within the first week of release and as of year-end 2011, has sold over 600,000 copies. A Remastered version was released for Microsoft Windows in December 2015 with plans for PlayStation 4 and Xbox One versions scheduled to be released in 2016.

Empire (1962 TV series)
Empire is an hour-long Western television series set on a 1960s 500,000-acre (2,000 km2) ranch in New Mexico, starring Richard Egan, Terry Moore, and Ryan O'Neal. It ran on NBC from September 25, 1962, to May 14, 1963.
In the second abbreviated season, from September 24 to December 31, 1963, it was renamed Redigo after Egan's title character, Jim Redigo, the general manager of the fictitious Garrett ranch in Empire, and reduced to a half-hour.
Cast
Egan starred in the series at the age of forty-one, having previously been in the hit film A Summer Place, with the catchy theme song. Redigo was a rare ranch manager, having a Master of Business Administration degree. The ranch was located somewhere in the American Southwest, but the exact location was never pinpointed. The Garretts did have an empire. Besides ranching they were involved in oil, agriculture, and mining. The series has unusually- titled episodes.
Empire also featured 22-year-old Ryan O'Neal, some two years before he gained greater recognition as Rodney Harrington in ABC's Peyton Place. O'Neal, who began acting in 1959, played the son, Tal Garrett. Terry Moore portrayed O'Neal's 33-year-old sister, Connie, who had a romantic interest in Redigo. Their mother and ranch matriarch, Lucia, was played by 53-year-old Anne Seymour (1909–1988).
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field that contains the base field and satisfies additional properties. For instance, the set Q(√2) = {a + b√2 | a, b ∈ Q} is the smallest extension of Q that includes every real solution to the equation x2 = 2.
Definitions
Let L be a field. A subfield of L is a subset K of L that is closed under the field operations of L and under taking inverses in L. In other words, K is a field with respect to the field operations inherited from L. The larger field L is then said to be an extension field of K. To simplify notation and terminology, one says that L / K (read as "L over K") is a field extension to signify that L is an extension field of K.
If L is an extension of F which is in turn an extension of K, then F is said to be an intermediate field (or intermediate extension or subextension) of the field extension L / K.

Degree of a continuous mapping
In topology, the degree of a continuous mapping between two compact oriented manifolds of the same dimension is a number that represents the number of times that the domain manifold wraps around the range manifold under the mapping. The degree is always an integer, but may be positive or negative depending on the orientations.
The degree of a map was first defined by Brouwer, who showed that the degree is homotopy invariant (invariant among homotopies), and used it to prove the Brouwer fixed point theorem. In modern mathematics, the degree of a map plays an important role in topology and geometry. In physics, the degree of a continuous map (for instance a map from space to some order parameter set) is one example of a topological quantum number.
Definitions of the degree
From Sn to Sn
The simplest and most important case is the degree of a continuous map from the 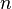 -sphere
-sphere  to itself (in the case
to itself (in the case 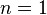 , this is called the winding number):
, this is called the winding number):
Let 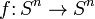 be a continuous map. Then
be a continuous map. Then 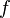 induces a homomorphism
induces a homomorphism 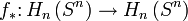 , where
, where 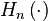 is the
is the 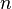 th homology group. Considering the fact that
th homology group. Considering the fact that  , we see that
, we see that 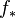 must be of the form
must be of the form 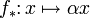 for some fixed
for some fixed 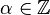 .
This
.
This 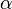 is then called the degree of
is then called the degree of 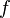 .
.
Degree of an algebraic variety
The degree of an algebraic variety in mathematics is defined, for a projective variety V, by an elementary use of intersection theory.
Definition
For V embedded in a projective space Pn and defined over some algebraically closed field K, the degree d of V is the number of points of intersection of V, defined over K, with a linear subspace L in general position, when
Here dim(V) is the dimension of V, and the codimension of L will be equal to that dimension. The degree d is an extrinsic quantity, and not intrinsic as a property of V. For example the projective line has an (essentially unique) embedding of degree n in Pn.
Properties
The degree of a hypersurface F = 0 is the same as the total degree of the homogeneous polynomial F defining it (granted, in case F has repeated factors, that intersection theory is used to count intersections with multiplicity, as in Bézout's theorem).
Other approaches
For a more sophisticated approach, the linear system of divisors defining the embedding of V can be related to the line bundle or invertible sheaf defining the embedding by its space of sections. The tautological line bundle on Pn pulls back to V. The degree determines the first Chern class. The degree can also be computed in the cohomology ring of Pn, or Chow ring, with the class of a hyperplane intersecting the class of V an appropriate number of times.
Podcasts:

