MSB: A mean-shift-based approach for the analysis of structural variation in the genome
- 1 Program in Computational Biology and Bioinformatics, Yale University, New Haven, Connecticut 06520, USA;
- 2 Department of Molecular Biophysics and Biochemistry, Yale University, New Haven, Connecticut 06520, USA;
- 3 Department of Molecular, Cellular, and Developmental Biology, Yale University, New Haven, Connecticut 06520, USA;
- 4 Department of Computer Science, Yale University, New Haven, Connecticut 06520, USA
Abstract
Genome structural variation includes segmental duplications, deletions, and other rearrangements, and array-based comparative genomic hybridization (array-CGH) is a popular technology for determining this. Drawing relevant conclusions from array-CGH requires computational methods for partitioning the chromosome into segments of elevated, reduced, or unchanged copy number. Several approaches have been described, most of which attempt to explicitly model the underlying distribution of data based on particular assumptions. Often, they optimize likelihood functions for estimating model parameters, by expectation maximization or related approaches; however, this requires good parameter initialization through prespecifying the number of segments. Moreover, convergence is difficult to achieve, since many parameters are required to characterize an experiment. To overcome these limitations, we propose a nonparametric method without a global criterion to be optimized. Our method involves mean-shift-based (MSB) procedures; it considers the observed array-CGH signal as sampling from a probabilitydensity function, uses a kernel-based approach to estimate local gradients for this function, and iteratively follows them to determine local modes of the signal. Overall, our method achieves robust discontinuity-preserving smoothing, thus accurately segmenting chromosomes into regions of duplication and deletion. It does not require the number of segments as input, nor does its convergence depend on this. We successfully applied our method to both simulated data and array-CGH experiments on glioblastoma and adenocarcinoma. We show that it performs at least as well as, and often better than, 10 previously published algorithms. Finally, we show that our approach can be extended to segmenting the signal resulting from the depth-of-coverage of mapped reads from next-generation sequencing.
Array-based comparative genomic hybridization (array-CGH) experiments (Solinas-Toldo et al. 1997; Pinkel et al. 1998) are used to detect and map chromosomal imbalances, which are common phenomena in cancers and other diseases. This technology has been applied successfully to study copy-number variants (CNVs) (Iafrate et al. 2004; Sebat et al. 2004), i.e., submicroscopic deletions and duplications, which commonly occur in the “normal” human population (Iafrate et al. 2004; Sebat et al. 2004; Tuzun et al. 2005). CNVs or microscopically visible larger amplifications and deletions may affect the transcription or, in some instances, the structure of genes in cis or in trans. As such, they may be responsible for phenotypic variation. In more extreme cases, these variations may cause cellular processes to malfunction, leading to diseases such as genetic disorders and cancer. For example, some particular types of observed genomic derangement reflect an underlying failure in the maintenance of genomic stability during the development of solid tumors. It is important to locate the chromosomal events that are responsible for human phenotypic variation and the pathogenesis of many diseases (Bredel et al. 2005; Pinkel and Albertson 2005).
Array CGH has become a powerful high-throughput technique. For instance, CGH arrays using bacterial artificial chromosome (BAC) clones have been broadly used. Nowadays, their resolution is in the order of 100 kb (Redon et al. 2006; Coe et al. 2007). cDNA and oligonucleotide arrays are also popular for CGH (Pollack et al. 1999; Brennan et al. 2004). The short probes on these arrays present a higher resolution of 25–100 kb (Coe et al. 2007). Recently, new technologies using tiling arrays were introduced for an even finer resolution. These techniques allow for the detection of microamplifications and deletions (Lucito et al. 2003; Ishkanian et al. 2004). In particular, high-resolution CGH (HR-CGH) has been developed (Selzer et al. 2005; Urban et al. 2006; Korbel et al. 2007a) and has been shown to accurately detect the presence and extent of CNV at resolutions up to 200 bp, in turn making it possible to sequence CNV breakpoints (Urban et al. 2006; Korbel et al. 2007a). The rapid development of the array-CGH technology challenges bioinformatics researchers to come up with methods for the accurate identification of chromosomal segments.
Array-CGH data consist of the log ratios of normalized fluorescence intensities (array readouts) from disease vs. control samples. The data are indexed by the physical location of the probes on the chromosome. The regions of interest are the concentrated high or low log ratios of intensities. These regions can be very small, which makes the identification of biologically relevant events challenging.
A variety of computational methods have been proposed for analyzing array-CGH data. Initially, a heuristic method was introduced by smoothing the ratio profiles using a moving average, and a threshold was applied to indicate the presence of amplification or deletion events (Pollack et al. 1999). Hughes et al. (2000) used a simpler error-weighted mean approach for genome-wide prediction of aneuploidy. Their heuristic scanning method identifies at least four contiguous overexpressed or underexpressed genes as potentially amplified or deleted segments.
Recently, following these proof-of-principle type approaches, more sophisticated algorithms for scoring CGH arrays have been developed. Many of these approaches are model-based; that is, they assume that there is a sequence of segments (amplifications or deletions) in the genome, which is itself a function of several prespecified parameters (e.g., the number and locations of breakpoints, and the mean and variance of each segment’s distribution). Typically, maximization of a likelihood function is used to estimate model parameters from the data. Different model-based approaches use different distribution assumptions and/or different definitions of the penalty term for the likelihood function. For instance, Hodgson et al. (2001) initially proposed a simple maximum likelihood method based on the assumption of a mixture of three Gaussian distributions, with each Gaussian referring to gain, loss, and normal regions, respectively.
More recently, Hupe et al. (2004) introduced a Gaussian model-based approach called GLAD, which uses a more complex likelihood function with weights determined adaptively to solve the estimation problem. Their estimation approach is coupled with an adaptive weights smoothing procedure. Furthermore, in another study, a genetic search algorithm was used to maximize the likelihood function (Jong et al. 2004), again using a penalty term that contains the number of breakpoints. Picard et al. (2005) used a penalized likelihood criterion to estimate breakpoints and to avoid the underestimation of the number of segments. In this method, known as CGHseg, the distribution assumption may have an important consequence in the model. A homogeneous variance assumption, among different regions, tends to result in a more segmented profile for maintaining the variance homogeneity between segments. The results may be more precise but can be more difficult to interpret (Picard et al. 2005). Yet another method called ChARM uses an edge filter to estimate the rough location of edges as an initial step. These edges are then located more accurately by an expectation maximization (EM) algorithm (Myers et al. 2004).
Concurrently, there are other model-based approaches using hidden Markov models (HMMs). These approaches assume that the underlying copy numbers are the hidden states with transition probabilities (Snijders et al. 2003; Fridlyand et al. 2004; Sebat et al. 2004; Korbel et al. 2007b; Stjernqvist et al. 2007). For instance, aCGH is a popular HMM-based package, which fits an unsupervised HMM to the data (Fridlyand et al. 2004): The state emission distributions are Gaussian with state-specific means and variances. K-means partitioning is used to estimate the means, and the transition probabilities are set proportional to copy number distance between pairs of states for initialization. Parameter optimization is performed with the Baum-Welch algorithm (an EM-like algorithm).
Model-based approaches usually employ a maximum likelihood estimate function for optimization, whereas global optimization is known to be hard to reach (Wand and Jones 1995; Comaniciu 2002). These approaches usually have to impose a distribution assumption. Moreover, many of these methods or their formulations are based on the EM algorithm (Snijders et al. 2003; Fridlyand et al. 2004; Myers et al. 2004; Picard et al. 2005; Stjernqvist et al. 2007), which has the some inherent drawbacks. First, it usually assumes a mixture of normal structures, which may not hold true under certain conditions. Furthermore, it requires the specification of the number of segments as an initialization step. Finally, its correct convergence becomes difficult when the number of clusters or states is large.
Here, we propose a nonparametric mean-shift-based method (MSB) to overcome these limitations. Our data-driven approach does not employ a global criterion that should be optimized, and it is not affected by the number of segments. It does not impose a distribution assumption in finding structures in the data. It effectively preserves the discontinuity and abrupt changes (breakpoints) through kernel density estimation and the mean-shift procedure, in which local neighborhoods are adapted to the local smoothness of the intensities measured by the observed data. The procedure can therefore remove the noise correctly in homogeneous regions of the chromosome and preserve discontinuities at the same time. We show the capabilities of this method to detect the segments of changed copy numbers in array-CGH data by applying it to both simulated data and published experimental data sets.
There are several other types of methods for CGH analysis. We compare our method to these as well as to the above model-based approaches, showing the advantages of our method. In particular, a common approach applied is based on locally weighted regression and smoothing of scatterplots (lowess) (Beheshti et al. 2003). Wavelet smoothing has been introduced, handling abrupt changes in the CGH profile (Hsu et al. 2005). Quantile smoothing (called quantreg) creates sharper boundaries between segments based on the minimization of errors in L1 norm (the sum of the absolute errors), rather than L2 norm (the sum of the squared boundary) (Eilers and de Menezes 2005). Olshen and Venkatraman proposed the circular binary segmentation (CBS) method, which recursively uses the maximum of the likelihood ratio statistics to detect narrower segments of aberrations (Olshen and Venkatraman 2002, 2004; Venkatraman and Olshen 2007). In addition, Wang et al. (2005) propose a hierarchical clustering-style tree to “cluster along chromosomes” (CLAC) so as to identify regions of interest. More recently, Klijn et al. (2008) identified cancer genes using a statistical framework for multiexperiment analysis of nondiscretized array-CGH data.
Finally, we show that because of the nonparametric and model-free nature of MSB, it can be readily be applied to a related problem of array-CGH—inferring structural variation (SVs) from the depth of coverage of mapped short reads coming from next-generation sequencing. We provide a brief proof-of-concept case study demonstrating this.
Methods
Overview
Our method to analyze array-CGH data is based on kernel density estimation and mean-shift theory. Array-CGH data are intensity measurements across the chromosome; these intensity measurements detected fluctuate around certain genomic copy levels due to noise and other factors. Model-based approaches usually make some probability distribution assumptions, which may not be true in certain circumstances, in order to infer the distribution. In statistics, kernel density estimation (also called “Parzen window method”) is a nonparametric way of estimating the probability density function (p.d.f.) (Wand and Jones 1995).
The density maxima in the distribution of intensities are the modes of the p.d.f., where the gradient of the estimated p.d.f. are zeros. The mean-shift method presents an elegant way to locate these density maxima without having to estimate the density directly (Comaniciu 2002). The mean-shift vector always points in the direction of maximum increase in the density. The mean-shift process is an iterative procedure that shifts each data point to these density maxima.
This nonparametric technique does not require prior knowledge of the number of segments or assumptions about probability distributions. The mean-shift approach performs the discontinuity-preserving smoothing on the array-CGH observation data through kernel density estimation and the mean-shift computation. This procedure can remove the noise effectively in homogeneous regions of the chromosome and preserve discontinuities at the same time.
Kernel density estimation and mean shift
The mathematical derivation of kernel density estimation theory was described by Wand and Jones (1995) and Comaniciu (2002). In pattern recognition, each sample is represented as a point in d-dimensional space, called feature space. Its dimension
is determined by the number of parameters (such as intensity and coordinate loci on the genome for array-CGH data) to describe
the sample points. The feature space can be regarded containing an empirical p.d.f. of the represented parameters. Given n data points xi (i = 1, . . . , n) in the d-dimensional space Rd, the multivariate kernel density estimator (
(x)) at point x is computed with kernel K(x) and a symmetric positive definite d × d bandwidth matrix H
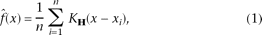where
In practice, the bandwidth matrix is often made either proportional to the identity matrix H = h2I or diagonal H = diag [h12, . . . , hd2]. For example, if we employ the former case, which provides one bandwidth parameter h > 0, we get
The kernel K(x) is a bounded function that must satisfy the following conditions (Wand and Jones 1995):
The radially symmetric kernel is a special case that satisfies K(x) = ck,dk(‖x‖2), where k(x) is the profile of the kernel (x ≥ 0). ck,d (assumed strictly positive) is the normalized constant that makes K(x) integrate to one. By introducing profile notation, the density estimator can be rewritten as
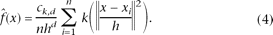The first step in the analysis of the feature space with underlying density f(x) is to find the modes of the density, which are among the zeros of the gradient ∇f(x) = 0. The mean-shift method is an elegant way to locate these zeros without having to estimate the density (Comaniciu, 2002). By computing, using the chain rule, the gradient of f(x) ∇ f(x), the Formula 4 is changed to
where g(x) = −k'(x) using simplified notation. The kernel G(x) then is defined as G(x) = cg,dk(‖x‖2), where cg,d is the corresponding normalization constant.
In Equation 5, the first factor 
g(‖(x − xi)/h‖2) is assumed to be a positive number. This condition is easy to satisfy for all the profiles in practice. The second factor
in Equation 5 is called the mean shift, which is the difference between the weighted mean (using the kernel G for weight) and the center
of the kernel x.
It has been proven that the mean-shift vector at location x computed with kernel G is proportional to the normalized density gradient estimate obtained by kernel K (Comaniciu 2002). The mean-shift vector always points toward the direction of the maximal increase in the density. The mean-shift procedure is carried out by successive steps between the computation of the mean-shift vector mh,G(x) and the translation of window by mh,G(x). It has been proven that this procedure is guaranteed to converge at a point nearby where the estimate has a zero gradient, if the kernel K has a convex and is monotonically decreasing.
Thus, the sequence of successive locations of kernel G, denoted by yj (j = 1,2, . . .) for each starting point xi (y1 = xi), can be computed as
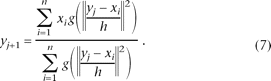Provided that the mean-shift vector always points toward the direction of the maximal increase in density, the local mean
is shifted toward the region in which the majority of the points are located. Consequently, the mean-shift vector can define
a path that leads to a stationary point of the estimated density, as it is aligned with the local gradient estimate. These
stationary points are called the modes of the estimated density. The meanshift procedure, obtained by consecutive computation
of the mean-shift vector mh,G(yj) and translation of the window yj+1 = yj + mh,G(yj), is guaranteed to converge to a point where the gradient of density function is zero. The set of all locations that converge
to the same mode defines “the basin of attraction” of that mode. The points that are in the same basin of attraction are associated
with the same cluster (Comaniciu 2002).
Kernels in array-CGH analysis
The multivariate kernel can be decomposed as the product of two radially symmetric kernels. In particular, the Euclidean metric
allows a single bandwidth parameter for each domain (Comaniciu 2002). For example, for CGH profiles, we may use
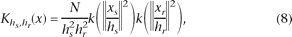where xs refers to the spatial position of the genomic probes in the CGH profiles (called spatial domain), xr is the log ratio of the intensity of hybridization (called range domain or intensity domain), k(x)is the common profile used on both domains, hr and hs are the employed kernel bandwidths, and N is the corresponding normalization factor. Without loss of generality, we used
the normal kernel in our CGH analysis. The profile function kN(x) = exp(−½x)(x ≥ 0) yields the multivariate normal kernel KN(x) = (2π)−d/2 exp(−½‖x‖2).
MSB-CGH method
Traditional smoothing algorithms replace the points in the center of a window by the weighted average of the window. Therefore, they indiscriminately blur the signals by removing not only the noise but also the salient information. MSB smoothing, by contrast, is based on the use of local information. It has been proven to be a discontinuity-preserving smoothing method, which adaptively reduces the amount of smoothing near abrupt changes (e.g., edges) in the local structures (Comaniciu 2002).
Let xi and zi be data points in the input and filtered output, respectively. For each point xi, assume that 
is the spatial-domain position in array-CGH profiles, while 
is the range domain (log ratio of the intensity measurement in CGH experiments). The mean-shift filtering process (Comaniciu 2002) is as follows:
-
Initialize j = 1 and y1 = xi
-
Compute yj+1 = (
g(‖(yj − xi/h)‖2)/
g(‖(yj − xi/h)‖2)) until convergence, we get yc.
-
Assign zi = (
, 
), which is the filtered data. This means that the filtered data at the spatial location 
will have the range component (or intensity domain for array-CGH) of the point of convergence 
.
The kernel in the mean-shift procedure moves in the direction of maximum increase in the joint density gradient. The key feature of the mean-shift procedure is the use of local information, which differentiates it from traditional smoothing methods. Each point is associated with a significant mode located in its neighborhood. The most important advantage of the mean-shift procedure is that points are attracted to the modes (local maxima) of the underlying density function. Therefore, it effectively preserves the discontinuities and promotes the breakpoint detection. We may straightforwardly extend the mean-shift procedure and define that the neighboring points on the chromosome attracted by the same mode in the intensity domain belong to the same segment of the CGH profiles.
Intuitive illustration of mean-shift procedures
A simplified example using data generated from glioblastoma samples from the study of Bredel et al. (2005) is illustrated in Figure 1. For simplicity, only a very short region (59 probes) from the glioblastoma data is shown, and the points are visualized sparsely.
Figure 1A illustrates the mean-shift process. The triangles show sets of successive locations (yj) from a starting point xi during the mean-shift iterations, starting from some exemplary original data points. The connecting lines show the mean-shift
vectors between successive locations. Figure 1B shows the mean-shift smoothing process; the triangles show sets of successive locations in the intensity domain (
in the second step of the filtering process) that converge to the same mode, i.e., the basin of attraction of that mode.
The figure shows that the points on the left side of the breakpoint boundary are attracted to the mode at the amplitude of
4.75, while the points on the right side of the breakpoint boundary are attracted by the mode at the amplitude of 0.2. Particularly,
the eighth and ninth points are attracted to different respective modes in the intensity domain. Therefore, this method preserves
the discontinuity and edges between the abrupt changes.
Mean-shift mode finding: A simple example of an array-CGH data segment from glioblastoma sample. (A) Mean-shift process: The successive set of triangles shows the yj, more particularly (
, 
), in the mean-shift iterations, while their connecting dashed lines show the mean-shift vector. (B) Mean-shift smoothing in the intensity domain: The successive set of triangles shows (
, 
), where 
refers to the spatial location, and 
refers to the intensity domain. The value zi = (
, 
) after convergence is the filtered data point. Here, we visualize only 59 points for the purpose of illustration. The data
represent a small segment of chromosome 7 of the GBM29 sample. The data consist of 67 probes among the nucleotide positions
ranging from 54,908,778–64,080,642 on chromosome 7 of GBM29. The points represent the actual measurements of the CGH experiments
along the chromosome segment. The straight lines show the results of MSB. The sets of successive locations shown by triangles
converge to the local modes of the intensity domain. The last one of these successive locations is the point of convergence
for each set. The eight points on the left side are attracted by the mode at the amplitude of 4.75 in the intensity domain, while the 51 points on the right are attracted by the mode at the amplitude of 0.2 in the intensity domain. Clearly, the eighth and ninth points (shown with
stars) are attracted by different modes separately.
Bandwidth selection
The resolution of the output of mean-shift segmentation is controlled by the kernel bandwidth. The analysis of the data set that exhibits multiscale patterns often requires kernel density estimation technique with locally adaptive bandwidth. We adopt a data-driven bandwidth selection algorithm. Its details were explained by Comaniciu (2003). Briefly, the fixed bandwidth mean-shift procedure with different analysis scales is applied at the initial step. For each scale, each data point is classified into a local mode. The trajectory points and mean-shift vectors are then used to fit a normal surface to the density surrounding each mode. The most stable covariance matrix across scales is then selected using a specialized version of the Jensen-Shannon divergence for each data point. At last, the covariance matrices are used in the variable-bandwidth mean shift. This data-driven bandwidth selection algorithm estimates the bandwidth for multiscale patterns in the data set. It has been proven to be applicable in both normal and non-normal structures. It has been proven to be a reliable algorithm that takes into account the stability of local bandwidth estimates across scales. In our experiments, we applied the data-driven band selection algorithm to the range domain (log ratio of intensities of CGH), while we empirically chose the anticipated minimum length of segments as bandwidth for the spatial domain on chromosomes. This only requires prior knowledge of a range of scales for the intensity domain, which is a practical criterion.
Simulated data sets
The simulation was carried out by generating aberrations involving five, 10, 20, and 40 probes (here referred to as width) with three different signal-to-noise ratio (SNR) levels (1, 2, and 4). The SNR is defined as the average magnitude of the signal divided by the standard deviation of the (superimposed) Gaussian noise. For each aberration width and SNR, 100 “artificial” chromosomes were generated. Each artificial chromosome consists of 100 probes. The aberrations were located in the centers of the chromosomes (Lai et al. 2005).
Application to the glioblastoma data set
We used glioblastoma multiforme (GBM) data from the study of Bredel et al. (2005), consisting of 26 primary GBM samples, which were cohybridized with pooled human controls onto custom spotted cDNA microarrays. The scanned raw data were deposited in the Stanford Microarray Database (http://genome-www5.stanford.edu). Lai et al. preprocessed the data and normalized the data with the Limma package (Smyth 2004). They also removed the missing values in each array to avoid the effect of imputed values in subsequent analyses (Lai et al. 2005). The GBM data are composed of a mixture of wide, low amplitude regions of gains/losses and narrow, high-amplitude regions of amplifications/deletions, both of which should be detected by algorithms scoring array-CGH data. Furthermore, these data are quite noisy (standard deviation of the log ratios for each array range from 0.35–0.9), providing a reasonable reference for examining different CGH algorithms. We chose to examine two representative samples (one with a broad, low-amplitude change and one with some narrow, high-amplitude changes) using MSB and other CGH analysis approaches.
Array-CGH algorithms for comparison
Eight CGH analysis algorithms were picked for the comparison based on the public availability of R statistical language implementation. These algorithms are CGHseg (Picard et al. 2005), GLAD (Hupe et al. 2004), wavelet (Hsu et al. 2005), CBS (Olshen and Venkatraman 2002, 2004; Hsu et al. 2005), lowess (Beheshti et al. 2003), quantreg (Eilers and de Menezes 2005), HMM (Fridlyand et al. 2004), and CLAC (Wang et al. 2005). CGHseg was ported from MATLAB to R by Lai et al. (2005). Additionally, we used their results from ChARM (Myers et al. 2004) on the simulation data sets for comparison purpose.
Default parameter settings were used when suggested by the investigators. Otherwise, appropriate parameters were selected or computed based on program documentation as well as related papers. These settings are consistent with a previous comparative study (Lai et al. 2005): For the wavelet algorithm, Stein’s unbiased risk estimate (SURE) for soft thresholding with a maximum wavelet coefficient level of 3 was chosen following the method of Hsu et al. (2005); for the lowess algorithm, a smoothing window of 10 was used, and the smoothing span was defined as the size of the smoothing window divided by the number of probes on the chromosome (Lai et al. 2005). Finally, for the quantreg algorithm, twofold cross-validation was used to estimate the value of λ that minimizes the overall penalty term as suggested by the investigators (Eilers and de Menezes 2005); λ was estimated as 1.5.
Results
Evaluation of MSB on simulated data
First, we compare MSB on the simulated abnormality widths and noise levels. The simulated data were generated by the various aberration widths and different noise levels, as described in detail in the Methods section. Figure 2 shows an example of the composed simulated CGH data with increased aberration widths (2, 5, 10, 25) and with noise σ = 0.25. We intuitively show how MSB works compared with nine other CGH analysis algorithms. In Figure 2 only MSB, HMM, and CGHseg detected all five aberrations correctly.
An example of simulated array-CGH data by composed aberrations with increasing width (2, 5, 10, 20, and 40 probes). This signal profile consists of five aberrations of width in increasing order. The amplitude of aberration is 1. Gaussian noise with σ = 0.25 was imposed onto the signal profile in the simulated data. MSB, CGHseg, and HMM clearly detected all five aberrations.
Receiver operating characteristic (ROC) analysis was carried out using the following conditions: The true positive rate (TPR) was defined as the number of probes within aberration regions, which have fitted values above the threshold level, divided by the total number of probes within aberration regions. The false positive rate (FPR) was defined as the number of probes outside the aberration regions, which have fitted values above the threshold level, divided by the total number of probes outside the aberration. The threshold for determining the aberration was altered from the minimum log-ratio value to the maximum in order to obtain sensitivities (i.e., TPR) at different specificity levels (FPR = 1 − specificity) for the ROC curve plots. For each simulation data set (i.e., given aberration width and SNR), the corresponding TPR (sensitivity) and FPR (1 − specificity) were plotted defining the algorithm’s ROC profile.
The comprehensive comparison of algorithms is shown in Figure 3. The upper left panels show scenarios with wider region aberrations and relatively low noise (high SNRs). It is evident that most algorithms performed well in detecting the existence and the width of aberrations in those situations. For the cases of smaller aberrations and low SNRs (the lower, right panels), MSB appears to outperform other methods (Lai et al. 2005), especially in the low FPRs (i.e., high specificity levels). Also, it is noticeable that the four smoothing-based methods (i.e., MSB, wavelets, lowess, and quantreg) give better detection results (higher sensitivity and specificity) than other methods in these cases. The smoothing-based algorithms follow low amplitude and local trends in the data; whereas the other six estimation algorithms were less sensitive to such features. The other six estimation algorithms (Lai et al. 2005) cannot detect the narrow and noisy aberrations reliably, presumably because the signal is too weak to differentiate it from the noise. MSB performs the best among these methods for aberration with small widths and low SNRs. MSB takes advantage of the mean-shift procedure, in which data points are attracted to the modes (local maxima) of the underlying density function. Therefore, this procedure adaptively reduces the amount of smoothing near the abrupt changes in the local structures. It filters and reduces noise without blurring the edges of the boundaries.
Receiver operating characteristic (ROC) analysis for array-CGH algorithms on simulation data sets. These data sets were simulated at different aberration widths and signal-to-noise ratios (SNRs). Each row represents three different SNR levels (4, 2, and 1, from top to bottom, respectively), and the columns represent aberration widths of 40, 20, 10, and 5 probes from left to right, respectively. The x-axis is 1 − specificity (the false positive rate) and the y-axis is the sensitivity (true positive rate). The curves were generated by measuring the sensitivity and specificity on simulated data at different threshold levels. The green curve refers to MSB. Its 90% confidence intervals are shown by the green bars for different levels. The blue curve is for CGHseg (Picard et al. 2005); the cyan point curve for GLAD (Hupe et al. 2004); the yellow dot curve for wavelet (Hsu et al. 2005); the solid yellow curve is for CBS (Olshen and Venkatraman 2002, 2004; Hsu et al. 2005); the magenta dot curve is for lowess (Beheshti et al. 2003); the blue dot curve is for quantreg (Eilers and de Menezes 2005); the red dot curve is for ChARM (Myers et al. 2004; Lai et al. 2005), the solid black curve is for HMM (Fridlyand et al. 2004); and the solid purple curve is for CLAC (Wang et al. 2005). The bottom right of each figure at SNR level 4 and 2 shows the zoom-in at the low false positive rate region.
Evaluation of MSB on glioblastoma data
GBM is a malignant type of brain tumor. The GBM data obtained in an earlier experimental study (Bredel et al. 2005) are relatively noisy. We examined two examples from the preprocessed GBM data (Bredel et al. 2005; Lai et al. 2005), which represent cases of narrow, high-amplitude and broad, low-amplitude changes, respectively.
Let us first examine the case with multiple amplitude changes on relatively small regions. There are three high-amplitude amplifications around the epidermal growth factor receptor (EGFR) gene on chromosome 7 (GBM29 sample). The nucleotide positions are from 40,640,694–64,966,234 (build 16), where there are sequentially 193 probes of length ranging from 99–123,181 on the corresponding chromosomal region. Only four probes separate the first two amplification regions. As shown in Figure 4, MSB, CGHseg, GLAD, wavelet, and quantreg detected all three amplifications correctly; CBS detected three amplified regions with the wrong amplitude; lowess detected the first two amplifications as one larger region, CLAC took all three amplifications as a single region, and the HMM-based algorithm did not detect any event. ChARM also failed to separate these three amplifications, as shown by Lai et al. (2005). CLAC and ChARM use mean smoothing as the initial step for filtering the data. However, the mean smoothing blurs the edges of the boundaries when it denoises the data. MSB adopts an advanced discontinuity-preserving filtering process. Therefore, the edges of the boundaries are effectively preserved.
Application of MSB and eight other methods to an array-CGH profile of the three amplifications around EGFR in the GBM29 sample. MSB, CGHseg, GLAD, wavelet, and quantreg clearly detected all three amplifications correctly. CBS detected three amplifications with the wrong amplitude. lowess only detected the first two amplifications as one larger region. CLAC took these three amplifications as one region. HMM performed the worst, with no detection.
Furthermore, in some instances, regions of loss or gain measured by array-CGH may exhibit a very low amplitude change and are thus hard to detect. In particular, since not all tumor cells in a given cell/tissue sample will have the same type of gain and/or loss, the overall amplitude change may be low due to the heterogeneity. For instance, in the GBM31 sample there is a large region of loss on chromosome 13 (from 17,206,847–113,010,904, a region covered by 797 probes) exhibiting a rather low SNR. Recognizing that it is obviously a challenge for array-CGH analysis approaches to detect such subtle changes, we tested the ability of MSB and eight other algorithms to detect this particular event (Fig. 5). MSB, CGHseg, GLAD, CBS, and HMM successfully identified the proximal loss of chromosome 13. CLAC, wavelet, quantreg, and lowess missed this subtle change. The other three smoothing algorithms (wavelet, quantreg, and lowess) failed to detect this subtle change, because the global loss was obscured by their smoothing process, while the mean smoothing step of the CLAC algorithm tended to reduce noise at the cost of blurring the edges of the boundaries. The successful segmentation of chromosome 13 by MSB indicates the power of our method, which preserves edges (i.e., discontinuities) while smoothing the data and removing noise.
Application of MSB and other eight methods to an array-CGH profile of chromosome 13 in a glioblastoma multiforme sample (GBM31). The profile has a partial loss with subtle amplitude change. MSB, CGHseg, GLAD, HMM, and CBS clearly identified this region.
Application of MSB to lung cancer data
We applied our method to array-CGH data from lung cancer cell lines, originally published by Coe et al. (2006) and Garnis et al. (2006). These data are particularly useful, as phenotypic patterns have been validated using PCR. To compare the output results of our method and other approaches, we ran the algorithms on the data. Figure 6 shows a comparison of the results of our method and eight other approaches on a data set of chromosome 2 of non-small cell lung cancer (NSCLC) adenocarcinoma. This data set contains 2592 BAC-derived tiling fragments, which covers 242,913,687 base pairs. It contains a region of wide amplification and a region of short deletion.
Output of MSB and eight other methods to an array-CGH data set of chromosome 2 in a NSCLC adenocarcinoma case. This profile contains a wide amplification region and a short deletion segment. MSB and CGHseg clearly identified these regions. A straightforward post-processing refined the MSB results.
MSB and CGHseg successfully identified these two aberrations, although the CGHseg result seems neater than that of MSB. However, MSB does not take any post-processing here. It indicates that GLAD and CBS identify these two major aberrations, but they show some hypersegmentation problems. This problem becomes much more serious in HMM and quantreg and the wavelet method. This recent lung cancer array-CGH data are much more challenging to standard segmentation approaches, where hypersegmentation is a known problem in this data. We can see that MSB and CGHseg suffer less from this problem than any other method. A simple post-processing step to overcome hypersegmentation is to group all the convergence points that are closer than the standard deviation of the noises in intensity measurement in the contingent region. An optional step, not taken here, is to eliminate spatial regions that contains less than the predefined number of probes. This segmentation post-processing would effectively eliminate the oversegmentation problem.
Proof-of-concept case study applying MSB to the pseudo-signal from next-generation sequencing
One of the strengths of MSB is that it does not have to refine an explicit model. Consequently, it can readily be applied to a related problem to array-CGH, determination of SVs from the high-throughput sequencing. This problem takes advantage of the great depth of coverage of the short reads from next-generation sequencing, which effectively creates pseudo-array signals to be partitioned. More specifically, new massively parallel sequencing techniques such as Illumina (formerly known as Solexa sequencing), 454 Life Sciences (Roche), and ABI SOLiD, have made possible resequencing and analysis of bacterial and individual eukaryotic genomes with extremely high coverage (http://www.1000genomes.org/) (Campbell et al. 2008; Durfee et al. 2008; Wheeler et al. 2008). Typical analysis of the high coverage data involves mapping of reads to a reference genome with the aim of identifying single nucleotide polymorphisms or structural variants. In the past, SV identification has involved looking for the change in spacing of paired end reads (Korbel et al. 2007a). However, here we suggest an alternate and complementary approach. The basic idea is that the regions that were deleted from the target genome will have no mapped reads, or just a few, due to errors in mapping. Conversely, regions that were duplicated will have considerably more mapped reads than the average coverage. Thus, we used nucleotide coverage depth (CD) of the reads as an input signal for MSB. This approach can be advantageous for SV identification over, for instance, genome comparison or paired-end mapping approaches, in that it can naturally utilize different reads (both paired-end and single reads of different length) and requires no assembly or paired-end clustering.
While different in origin to array-CGH signal, the CD signal is mathematically very similar to it. Similar to the array-CGH-signal, it will have regions of high and low intensities caused by SVs and repetitions in compared genomes. Likewise, it will have noise caused by mapping errors and random fluctuations in genome coverage.
Thus, CD creates an array-like pseudo-signal that can be analyzed for breakpoints in a similar fashion to array-CGH data. To provide a simple proof-of-concept demonstration of the application of MSB to this type of data, we have utilized a data set of mapped Illumina paired-end reads for NA11995. This individual was sequenced by the Sanger center as part of the 1000 Genomes Project. Mapping was performed with the aid of MAQ software (Li et al. 2008) with redundant reads excluded from the final mapping. We regard the choice of the data set as a representative one and stress that the method can be easily applied to other data sets as well (Korbel et al. 2007a; Campbell et al. 2008; Durfee et al. 2008).
We limited our analysis to a relatively small region on chromosome 21 (between coordinates 46,162,500 and 46,164,711). Given the mapped locations of reads, the CD-signal was constructed by counting the frequency of mapped reads for each nucleotide; then MSB was applied to the CD-signal (Fig. 7). Our approach could readily identify a number of potential SVs as shown in the figure.
Proof-of-concept application of MSB to Illumina CD signal on a part of chromosome 21. The data is from position 46,162,500–46,164,711 on the x-axis. The y-axis shows the half representation of frequencies (actual frequencies are multiplying the numbers by 2). Light color shows the experimental results. MSB identified several regions of changed copy number, shown in black lines.
Discussion
MSB shows excellent performance on both simulated data sets and real data sets of the GMB. It was consistently successful in meeting various detection challenges: different levels of SNRs and aberration width in the simulated data sets (ranging from “easy” large changes with high SNRs to “hard” small changes with low SNRs), mixed aberration widths in one simulated profile, multiple amplitude changes within relatively small regions in human cancer sample, and a broad, low-amplitude change on a human cancer sample. MSB consistently gives excellent results under different scenarios. Moreover, the model-free nature of MSB allows it to be readily adapted to the next generation sequencing data.
We are of course aware of the inherent difficulty in comparing different algorithms objectively. Each method has its own parameters, which may not have been set to optimum values. Furthermore, previously reported algorithms were developed to score array-CGH data from different experimental platforms, that is, at distinct resolutions, and different SNRs. Thus, to a certain extent, comparative studies should be taken with caution. We have attempted to follow the investigators’ instructions and previous comparative studies for setting parameters (Olshen and Venkatraman 2002, 2004; Beheshti et al. 2003; Snijders et al. 2003; Fridlyand et al. 2004; Hupe et al. 2004; Eilers and de Menezes 2005; Hsu et al. 2005; Lai et al. 2005; Picard et al. 2005; Wang et al. 2005; Venkatraman and Olshen 2007). It may be safe to suggest, however, that if an algorithm is sensitive to changes in parameters or if it is very difficult for users to determine the correct parameters, then one may consider this is a weakness of the method.
The time complexity of MSB is Ο(n2), where n is the number of probes along the chromosome. The space complexity of MSB is Ο(n). The time complexity is equivalent to the complexities of the HMM-based method and the CBS approach. Nevertheless, MSB will be slower than some fast local algorithms that run in time Ο(n), such as lowess and wavelet. Generally, speed is not a concern for BAC arrays. In the case of high-density oligonucleotides tiling arrays, where speed is one of the primary requirements, MSB can be accelerated by selecting a set of q representative data points using an irregular tessellation approach (Comaniciu and Meer 1999) and only computing the trajectories of those points (Comaniciu 2003). This is particularly useful for large regions without aberrations obtained by some simple preprocessing steps. In this case, the time complexity of MSB can be decreased to Ο(qn), where q < < n.
Recently, Eilers and de Menezes (2005) suggested that, for significance testing, many issues arise in connection with array-CGH data in general. The reason is that statistical significance refers to the consistency of effects. Namely, effects should occur in a proportion large enough to rule out chance. However, in the most important applications of array-CGH, such as carcinogenesis studies, most effects occur in a much too small proportion of the cases (Nakao et al. 2004). Additionally, changes detected with array-CGH should be validated by confirmatory experiments. In fact, the assessment for verifying patterns is almost always made based upon the biological context, rather than on the P-values in CGH analysis. Consequently, statistical significance testing in this context is unlikely to be helpful (Eilers and de Menezes 2005). For this reason, we have deliberately abstained from significance testing.
Generally, the limitation of the approach based on mean-shift and kernel density estimation is that it does not scale well with the dimension of the space. It has been indicated that when the dimensionality is above six, the analysis should be approached carefully (Wand and Jones 1995; Comaniciu 2002). Array-CGH data are low-dimensional and thus very suitable for our method.
Conclusion
We have demonstrated the general applicability of MSB in array-CGH analysis. Moreover, we have shown through a brief case study that the generality and model-free nature of MSB makes it potentially applicable to next generation sequencing data. We envision that a more sophisticated software suite for MSB can be developed. For instance, the physical position of probes may be incorporated into the approach (instead of using the index number of the probes without the actual spacing information) to increase the sensitivity of the method. Second, MSB, which essentially performs discontinuity-preserving smoothing, may be coupled with a more advanced segmentation approach. For example, the mean-shift segmentation algorithm (Comaniciu 2002) and downstream analysis may be implemented subsequent to smoothing. This can lead to an advanced variant of MSB. Third, a speedup module using irregular tessellation can be used to accelerate the data processing, which is particularly useful when applied to a large-scale data set with speed requirement. Finally, to facilitate application of the method for biomedical researchers, a graphical user interface (GUI), visualization graphics, online database connections, and annotation systems are desirable. These more advanced features will be integrated with our core algorithm in a future publication.
Acknowledgments
We thank the anonymous reviewers for their advice and comments. This work was supported by the NIH. We thank Dr. P. Park and his colleagues and the 1000 Genomes Project for data. We also thank Pedro Alves and Amittai Aviram for reviewing this manuscript and providing comments.
Footnotes
-
↵5 Corresponding author.
↵E-mail mark.gerstein{at}yale.edu; fax (203) 432-6946.
-
Article published online before print. Article and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.080069.108.
-
- Received April 23, 2008.
- Accepted September 24, 2008.
- Copyright © 2009, Cold Spring Harbor Laboratory Press
