The physics case of a 3 TeV muon collider stage
- de Blas, Jorge et al
- arXiv:2203.07261FERMILAB-CONF-22-317-AD-ND-PPD-SCD-TD
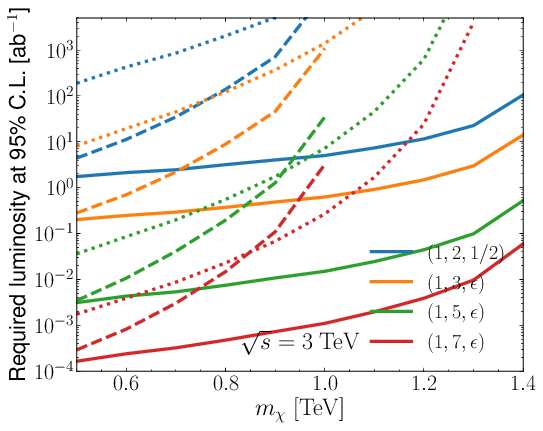
 | Signal statistical significance for various IDM benchmark points~\cite{Klamka:2022ukx} at high energy lepton collider for charged Higgs pair production and semi-leptonic final states. |
 | Signal statistical significance for various IDM benchmark points~\cite{Klamka:2022ukx} at high energy lepton collider for charged Higgs pair production and semi-leptonic final states. |
 | The kinematic distributions $\theta_B,R_{BB},M_{3B}(B=Z,H)$ of $ZZH$ (left) and $ZZZ$ (right) production at a $\sqrt{s}=10$ TeV $\mc$. |
 | The kinematic distributions $\theta_B,R_{BB},M_{3B}(B=Z,H)$ of $ZZH$ (left) and $ZZZ$ (right) production at a $\sqrt{s}=10$ TeV $\mc$. |
 | The kinematic distributions $\theta_B,R_{BB},M_{3B}(B=Z,H)$ of $ZZH$ (left) and $ZZZ$ (right) production at a $\sqrt{s}=10$ TeV $\mc$. |
 | The kinematic distributions $\theta_B,R_{BB},M_{3B}(B=Z,H)$ of $ZZH$ (left) and $ZZZ$ (right) production at a $\sqrt{s}=10$ TeV $\mc$. |
 | The kinematic distributions $\theta_B,R_{BB},M_{3B}(B=Z,H)$ of $ZZH$ (left) and $ZZZ$ (right) production at a $\sqrt{s}=10$ TeV $\mc$. |
 | The kinematic distributions $\theta_B,R_{BB},M_{3B}(B=Z,H)$ of $ZZH$ (left) and $ZZZ$ (right) production at a $\sqrt{s}=10$ TeV $\mc$. |