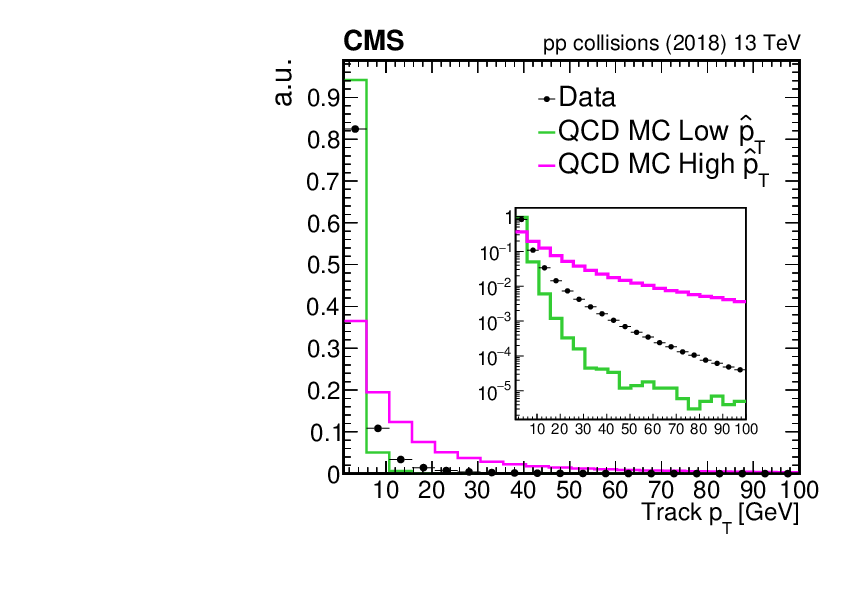
 | Normalized track \pt (left) and $\eta$ (right) distributions for the inclusive L1 trigger (top), $\Ztomm$ (middle), and interfill cosmic ray muon (bottom) data sets in arbitrary units. Data collected with the CMS detector in 2018 and used for the final alignment in that year (solid black circles) are compared with the simulation (solid coloured lines). Distributions in data are obtained from a sample of $11\times 10^6$, $55\times 10^6$, and $3.4\times 10^6$ tracks for the inclusive L1 trigger, $\Ztomm$, and cosmic ray muon data sets, respectively. For the inclusive L1 trigger data set, data are compared with two sets of simulated QCD events with different ranges of transverse momentum transfers $\pthat$. The green line corresponds to $\pthat$ between 15 and 30\GeV, whereas the magenta line corresponds to $\pthat$ between 1000 and 1400\GeV. The inset in the \pt distribution of the inclusive L1 trigger data set (top left) shows the same distribution with a logarithmic scale for the $y$ axis. No correction for the limited modelling of the trigger efficiency in the simulation has been applied for the $\Ztomm$ data set. The statistical uncertainty is smaller than the symbol size and therefore imperceptible. |