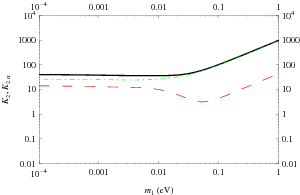
| Case $V_L=V_{CKM}$, NO. Plots of the relevant quantities for three choices of the involved parameters. The long-dashed red lines correspond to $\a=\t$, the dashed blue lines to $\a=\m$ and the short-dashed dark yellow lines to $\a=e$. Left panels: $\a_2=4$, $\theta_{13}=1.7^{\circ}$, $\theta_{12}=33.6^{\circ}$, $\theta_{23}=41.8^{\circ}$, $\d=2.84$, $\rho=$1.53 $\sigma=3.24$, $\rho_L=0.12$, $\sigma_L=2.56$; central panels: $\a_2=5$, $\theta_{13}=3.3^{\circ}$, $\theta_{12}=35.6^{\circ}$, $\theta_{23}=40.4^{\circ}$, $\d=-1.06$, $\rho=2.87$, $\sigma=6.0$, $\rho_L=3.13$, $\sigma_L=3.25$; right panels: $\a_2=4$, $\theta_{13}=4.7^{\circ}$, $\theta_{12}=35.9^{\circ}$, $\theta_{23}=40.3^{\circ}$, $\d=-1.89$, $\rho=0.065$, $\sigma=4.85$, $\rho_L=5.89$, $\sigma_L=3.69$. |